Implémentation et simulation de Boucles de Régulation avec le PID
Université des Sciences et de la Technologie d’Oran, Mohamed Boudiaf
Faculté de génie électrique département d’électronique
Ministère de l’Enseignement Supérieur et de la Recherche Scientifique
Spécialité : Electronique
Option : Maintenance des systèmes et Contrôle de Processus
Mémoire de projet de fin d’études pour l’obtention du diplôme de MASTER Professionnel.
Implémentation et simulation de Boucles de Régulation avec le PID et la logique floue sous Step7 et WinCC.
Présenté par :
Mlle. Wafaà BENALI OUENZAR
KREDOUDA Hanane
Encadré par : Mr W. NOUIBAT.
Membre de jury composé de :
Mr. BELALIA Président.
Mr. RIMA Examinateur.
Soutenu le :
24 juin 2013
Année Universitaire :
2012/2013
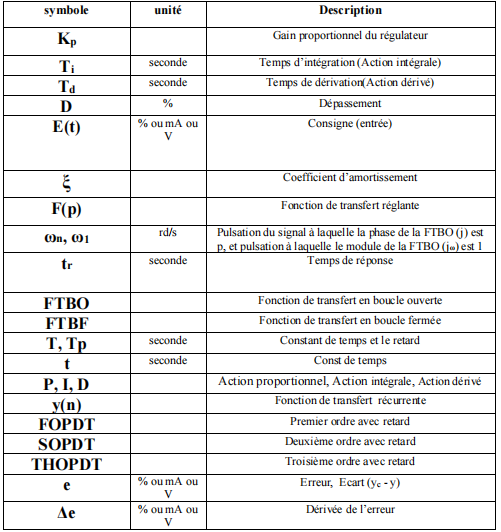
Notation et Sumboles
Chapitre I : Généralités sur la régulation
Introduction Générale
Le régulateur le plus utilisé dans l’industrie est le régulateur PID (proportionnel intégral dérivée), car il permet de régler à l’aide de ses trois paramètres les performances (amortissement, temps de réponse) d’une boucle de régulation d’un processus quelconque.
Nombreux sont les systèmes physiques qui même en étant complexes, le régulateur PID est bien adapté à la plupart des processus de type industriel et est relativement robuste par rapport aux variations des paramètres du procédé, quand on n’est pas trop exigeant pour les performances de la boucle fermée par rapport à celles de la boucle ouverte (par exemple, accélération très importante de la réponse ou augmentation très importante de l’amortissement en boucle fermée).
Si la dynamique dominante du système est supérieure, ou si le système contient un retard important ou plusieurs modes oscillants, le régulateur PID n’est plus adéquat et un régulateur plus complexe (avec plus de paramètres) doit être utilisé, aux dépends de la sensibilité aux variations des paramètres du procédé.
La réalisation d’une boucle d’asservissement par PID est un problème très important, car il influence :
- La qualité de la régulation sur un site industriel.
- Le réglage du régulateur PID, pour lequel la connaissance d’un modèle dynamique du procédé d’une part et les performances désirées d’autre part déterminent le choix de la méthode de synthèse.
- l’implantation du régulateur dans une version analogique ou numérique et dans une configuration série, parallèle ou mixte.
Le but de ce projet de fin d’étude est l’étude de boucles de régulation avec le PID et la logique floue (sous Matlab) puis son implémentation et simulation sous le logiciel de programmation STEP7 et de supervision WinCC des automates programmables industriels de Siemens.
Le premier chapitre est dédié aux quelques définitions sur la régulation avec le PID.
Le deuxième chapitre est consacré à la présentation du STEP7 et S7-300.
Le troisième chapitre, est consacré à la présentation de la logique floue.
Le quatrième chapitre présente une méthodologie pour la conception du bloc du procédé et du contrôleur flou dans le langage SCL sous step7.
Le cinquième chapitre donne les résultats de simulation des systèmes sous MATLAB et STEP7 et WINCC avec PID classique.
Le sixième chapitre est réservé à la présentation des résultats de simulation des systèmes sous MATLAB et STEP7 et WINCC avec le contrôleur flou.
Enfin, la dernière partie conclue ce mémoire. Nous y dressons un bilan final de notre travail.
I-Introduction
Dans un dispositif technique, le procédé de régulation a pour rôle d’amener une grandeur physique à prendre une valeur fixée à l’avance et de l’y maintenir.
Cette grandeur physique s’appelle grandeur réglée ou mesure elle peut être de nature très variable. Il peut s’agir par exemple :
- De grandeurs électriques : tension, courant, puissance, etc…
- De grandeurs mécaniques ou hydrauliques : pression, nombre de tours/min, débit, niveau, etc…
- De grandeurs thermiques : température, quantité de chaleur etc…
- De toute autre grandeur physique. La valeur fixée à l’avance, à la quelle e la régulation doit amener la grandeur réglée, s’appelle consigne de régulation.
Dans une régulation, on mesure d’une manière continue la grandeur réglée et on la compare à la consigne de régulation.
Dès qu’on détecte un écart entre elles, on produit dans le système une modification appropriée, qui doit ramener la grandeur réglée en accord avec la consigne de régulation. La grandeur subissant cette modification s’appelle : grandeur réglante.
Cela peut être une grandeur physique quelconque, par exemple la position d’ouverture d’une vanne, rangé de conduction des thyristors d’une unité de puissance, le rapport cyclique d’enclenchement d’un contacteur.
Il faut néanmoins choisir, comme grandeur réglante dans un système, une grandeur telle que sa variation agisse directement sur la valeur réglée. Dans la régulation, on distingue deux notions :
A-Régulation manuelle (commande manuelle)
La modification sur la grandeur réglante peut être effectuée par un opérateur observant continuellement la grandeur réglée en modifiant en conséquence la grandeur réglante. Dans ce cas on est en présence d’une commande manuelle tel est, par exemple le cas dans la conduite d’un bateau ou d’une automobile.
B-Régulation automatique (commande automatique)
Dans ce cas, la mesure de la grandeur réglée et la modification de la grandeur réglante s’effectue automatiquement au moyen d’appareil s’appelé régulateurs dans les quels est implanté une loi commande (algorithme). En régulation automatique Il n’y a donc pas d’intervention d’un opérateur humain.
C-Analyse des activités dans une chaîne de régulation
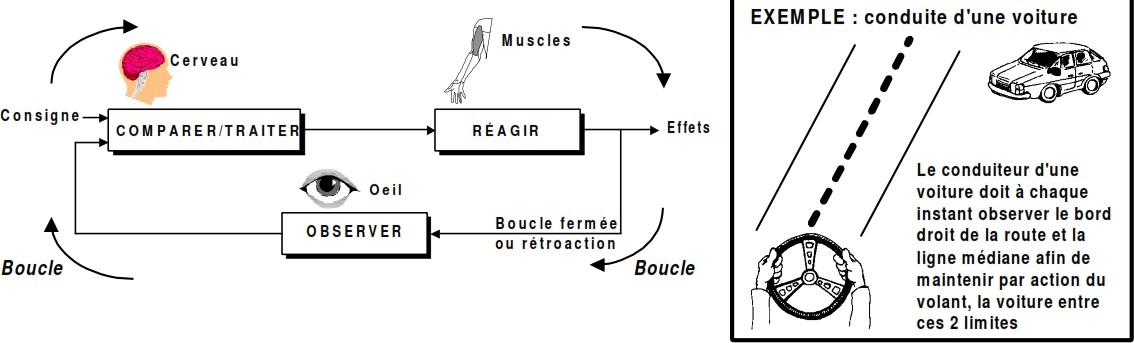
Fig.I.1 Analyse des activités dans une chaîne de régulation
I.1- Objectif de la régulation
L’objectif d’une régulation ou d’un asservissement est d’assurer le fonctionnement d’un procédé selon les critères prédéfinis par un cahier de charges. Les aspects de sécurité du personnel et des installations sont à prendre en compte comme ceux concernant l’énergie et le respect de l’environnement.
Le cahier des charges définit des critères qualitatifs à imposer qui sont traduits le plus souvent par des critères qualitatifs, comme par exemple, de stabilité, de précision, de rapidité ou de lois d’évolution. Voici quelques exemples d’objectifs qualitatifs :
- Obtenir une combustion air-gaz correcte dans un brûleur.
- Maintenir une qualité constante d’un mélange de produits.
- Obtenir un débit de fluide constant dans une conduite en fonction des besoins.
- Faire évoluer une température d’un four selon un profil déterminé.
I.2- Définition de la régulation/asservissement
Lorsqu’il y a un retour d’information de la grandeur observée sur le régulateur, on parle d’un asservissement du système ou d’une régulation du système.
I.2.1- Asservissement
La consigne, traduisant l’objectif désiré du procédé, n’est pas constantes et les grandeurs perturbatrices n’existent pas ou sont très peu influentes sur la grandeur à maîtriser.
I.2.2- Régulation
La consigne, traduisant l’objectif désiré du procédé, est constante et les grandeurs Perturbatrices influencent fortement la grandeur à maîtriser.
I.3-Définition de La régulation selon la norme DIN 19226
Selon la norme DIN 19226 sur les techniques de régulation, la commande est le processus dans un système par lequel une ou plusieurs grandeurs, appelées grandeurs d’entrées, influent sur d’autres grandeurs, appelées grandeurs de sorties, selon les lois propres au dit système.
La grandeur à réguler est mesurée de façon continue et est ensuite comparée avec une Valeur donnée en entrée du système. La régulation devra, en fonction du résultat de la comparaison, rapprocher la valeur à réguler de celle donnée en entrée.
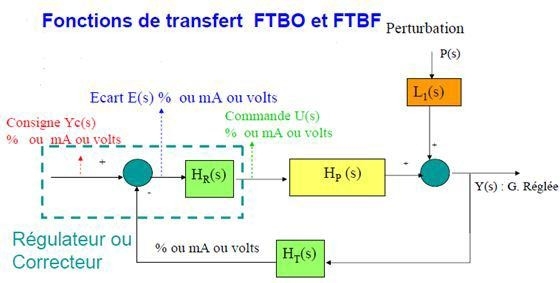
Fig.I.2 Schéma de régulation
L1(s). F. T perturbatrice. (Perturbation (P) >> Grandeur réglée G.R.
Hp(s).F.T procédé. (Commande Grandeur réglé).
Ht(s). F. T du capteur-transmetteur (mA/ (unité G.R).
Hr(s). F. T du régulateur ou correcteur.
I.4-Composition d’une boucle de régulation
Dans le paragraphe suivant vont être expliqués un par un les termes spécifiques aux techniques de régulations tels que « valeur de consigne », « valeur de sortie » … etc.
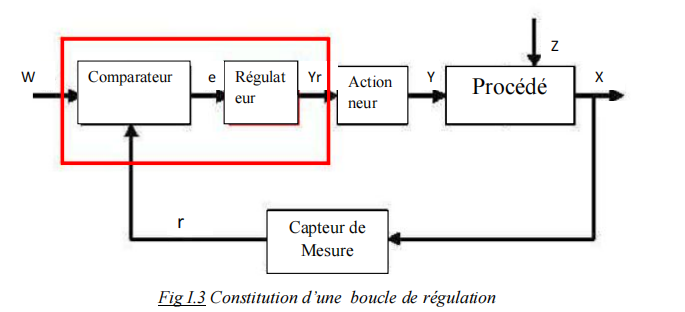
I.4.1 Sortie x
Elle est le résultat de la régulation, la variable que le système va influer et/ou essayer de garder constante.
I.4.2 Retour r
Dans une boucle de régulation, la sortie est constamment contrôlée, il est ainsi possible de réagir à toute variation indésirable de celle-ci. La valeur mesurée (proportionnelle à la sortie) est appelée retour (ou mesure).
I.4.3 Consigne w
La consigne est la grandeur qui doit commander la sortie, c’est à dire la valeur vers laquelle celle-ci doit tendre, pour finalement l’égaler. Si la consigne est constante, la sortie doit le rester (comportement statique).
Au contraire si celle-ci change, le but de la régulation dynamique est alors de reproduire les changements de consigne le plus fidèlement possible au niveau de la sortie.
Remarque la consigne n’a pas la même dimension que la sortie, elle doit être en accord avec la dimension de la mesure.
I.4.4Perturbation z
La perturbation est la grandeur qui influe de manière indésirable sur la sortie et qui l’éloigne de la valeur souhaitée (consigne). La seule existence d’une perturbation rend nécessaire la mise en œuvre d’une régulation statique.
I.4.6 Comparateur
C’est l’endroit où la mesure actuelle de la sortie et la valeur de la consigne sont comparées. Dans la plupart des cas les deux grandeurs sont des tensions. La différence des deux grandeurs ainsi obtenue est appelée erreur e. La valeur de l’erreur est passée en entrée du régulateur pour y être traitée.
I.4.6 Régulateur
Le régulateur est l’élément central d’une régulation. Il évalue l’erreur calculée par le comparateur, c’est à dire l’écart entre la sortie et la consigne, et en déduit à partir de celle-ci une valeur régulée ou valeur de correction à transmettre au procédé, afin de corriger la sortie.
I.4.7 Actionneur
L’actionneur est en quelque sorte, l’organe exécutif“ de la régulation. Il reçoit la variable régulée du régulateur. Cette variable d’entrée lui permet de savoir comment il doit influer sur la sortie de la régulation.
I.4.8 Procédé
Le procédé est le cœur du système régulé ou encore la partie originelle. C’est également la partie qui agit directement sur la valeur de sortie.
I.4.9Système régulé
Le système régulé est le système où se trouve la grandeur à réguler.
1.4.10 Retard ou temps mort
Le temps mort est le temps nécessaire pour qu’une modification de la sortie du régulateur provoque un changement mesurable de la sortie régulée.
I.4.11 Boucle de régulation
Réaction d’une boucle de régulation à la modification des grandeurs d’environnement.
Sommaire
Liste de figures… 7
Notation et symbole 10
Introduction générale 11
CHAPITRE I : GENERALITES SUR LA REGULATION 12
I: Introduction 12
I.1- Objectif de la régulation 13
I.2- Définition de la régulation /asservissement 13
I.2.1- L’asservissement 13
I.2.2- La régulation 13
I.3- Définition de La régulation selon la norme DIN 1922 13
I.4- Composition d’une boucle de régulation 14
1.4.1 Sortie x 14
1.4.2 Retour r 14
1.4.3Consigne w 14
1.4.4Perturbation z 14
1.4.5Comparateur 15
1.4.6Régulateur 15
1.4.7Actionneur 15
1.4.8Procédé 15
1.4.9Système régulé… 15
1.4.10Retard ou temps mort 15
1.4.11Boucle de régulation 15
I.5- Qualités attendues d’une régulation 15
1.5.1Stabilité… 15
1.5.2Précision 16
1.5.3Rapidité 16
I.6- Régulation en boucle ouverte/ en boucle fermée 16
1.6.1En boucle ouverte… 16
1.6.2En boucle fermée… 16
I.7- Régulation PID 17
1.7.1Régulateur proportionnel (Type P) 17
1.7.2Régulateur intégral (type I) 18
1.7.3Régulateur de type PI 19
1.7.4Régulateur dérivé (type D) 19
1.7.5Régulateur PID… 20
I.8- Type de régulateurs 20
1.8.1Régulateur tout ou rien 20
1.8.2Les régulateurs continus 21
1.8.3Régulateurs numériques… 21
1.8.4Régulation de rapport… 20
I.9- Choix et paramétrage du régulateur 22
I.10- Synthèse des systèmes asservis 23
1.10.1Performances d’un système asservi 23
1.10.2Réponse indicielle 24
I.11- Réalisation d’un PID sous STEP7 avec le bloc de régulation continue (S)FB41″CONT_C » 24
1.11.1Régulateur PID, données du problème 24
1.11.2Description 25
1.11.3Etats de fonctionnement 25
I.11.4-Informations d’erreur 25
I.12- Identification du procédé 25
1.12.1Identification en boucle fermée 25
1.12.2Méthode de Broida… 26
I.13- Avantages et inconvénients du correcteurs P, PI, PD et PID 27
I.14- Conclusion 27
CHAPITRE II : LA LOGIQUE FLOU 28
II.1- Introduction à la logique floue. 28
II.2- Commande flou d’un procédé 28
II.3- Principe de la logique floue 28
II.3.1 Introduction 28
II.3.2. Variables floues… 29
II.3.3Règles d’inférence 30
II.3.4Fonctions d’appartenance 30
II.4- Combinaison des règles et défuzzification 31
II.4.1Défuzzification 31
II.4.2Défuzzification par calcul du centre de gravité… 31
II.5- Régulateurs flous de type Mandani 32
II.6- Régulateurs flous de type Sugeno 33
II.7- Régulateurs flou de type PD et PI 33
II.8- Avantage et inconvénients des régulateurs PID et floue 34
II.9- Conclusion 34
CHAPITRE III : API ET STEP7 35
III.1. STEP 7 35
III.2. Logiciel de base STEP 7 35
III.3. Fonctions du logiciel de base 35
III.4 Applications disponibles 35
III.5-Langages de programmation 36
III.6- Domaine d’application de S7-SCL 36
III.6.1Fonctionnement de S7-SCL… 37
III.6.2Structure de programme S7-SCL… 37
III.6.3Rangement des blocs dans des sources S7-SCL 38
III.7- Langages évolués 39
III.8- Logiciels exécutables 39
III.9- Régulations pour SIMATIC S7 40
III.9.1-Contrôle PID standard 40
III.9.2-Contrôle PID modulaire 40
III.9.1 Composants SIMATIC 40
III.10- API (automate programmable) 40
III.10.1SIMATIC S7-300 41
III.10.2Modules susceptibles de faire partie d’un système d’automatisation modulaire S7-300 41
III.10.3Remplacement des modules simples et sans interversion 42
III.10.4S7-300 dispose de diverses interfaces de communication 42
III.10.5CPU d’API S7-300 42
III.10.6Logiciel STEP7 de programmation du S7-300 43
III.11- Automatisation sur PC : Soft-API WinCC 45
III.12 Présentation synoptique de la « DCS »… 46
III.13-Conclusion 46
CHAPITRE IV : PROGRAMMATION SOUS STEP7 47
IV.1- Création des blocs des systèmes 1ers, 2eme et 3ème ordre sous step7 47
IV.1.1Introduction 47
IV.1.2Création de bloc du 1er ordre sous STEP7 47
IV.1.3Création de bloc du 2eme ordre sous STEP7 48
IV.1.4Création de bloc du 3eme ordre sous STEP7 49
IV.2- Implémentation du contrôleur flou sous step7 50
IV.2.1Introduction 50
IV.2.2Programmation du contrôleur flou 51
IV.2.3Règles flou 52
IV.2.4Définition et évaluation des fonctions d’appartenance 52
IV.2.5Calcule la sortie floue de contrôleur de type sugeno (Agrégation) 53
IV.3- Identification de système en boucle ouverte 54
IV.3.1Constitution du Système 54
IV.3.2 Problème d’identification 54
IV.3.3Calcul de la fonction de transfert de procédé industriel à l’aide de BROIDA 55
IV.3.4Ajustement de paramétrage de PID avec la méthode de COHEN et COON 56
IV.3.5Système 1er ordre avec retard avec le PID classique sous MATLAB 57
IV.3.6Système en boucle fermée avec retard de 13.82s sous STEP7 58
IV.3.7Système du 1er ordre avec retard avec le PI flou sous MATLAB 58
IV.3.8Système du 1er ordre avec retard sous WINCC 59
Conclusion 60
CHAPITRE V : RESULTATS DE SIMULATION AVEC PID CLASSIQUE 61
V.1 Réponse du système du 1er ordre avec et sans retard 61
V.1.2-Réponse du système du 1er ordre en boucle ouverte sous WinCC 61
V.1.1-Réponse du système du 1er ordre sans retard en boucle ouverte sous MATLAB 61
V.1.3 Configuration du block OB35 pour avoir la réponse du 1er ordre… 61
V.1.4-Réponse du système du 1er ordre en boucle ouverte sous WinCC 63
V.1.5-Réponse du système du 1er ordre en boucle fermée sous MATLAB (sans retard) 63
V.1.6-Réponse du système du 1er ordre en boucle fermée sous STEP7 (sans retard) 64
V.1.7-Réponse du système du 1er ordre en boucle fermée sous WinCC (sans retard) 65
V.1.8-Réponse du système du 1er ordre en boucle fermée sous MALAB (avec retard de 2s) 65
V.1.9-Réponse du système du 1er ordre en boucle fermée sous STEP7 (avec retard de 2s) 66
V.1.10-Réponse du système du 1er ordre en boucle fermée sous WinCC (avec retard de 2s) 66
V.2- Réponse du système du 2éme ordre avec et sans retard 67
V.2.1Paramètre de la fonction de transfert de 2eme ordre 67
V.2.2Ajustage des gains de régulateur P, PI, PID selon la méthode de ZIEGLER_-NICHOL.S… 67
V.2.3Réponse de système du 2eme ordre en boucle ouverte sous MATLAB 68
V.2.4Réponse de système du 2eme ordre en boucle ouverte sous WINCC 68
V.2.5Réponse de système du 2eme ordre avec PID en boucle fermée sous MATLAB (sans retard) 69
V.2.6Réponse de système de 2eme ordre avec PID en boucle fermée sous STEP7 (sans retard) 69
V.2.7Réponse de système du 2eme ordre avec PID en boucle fermée sous WINCC (sans retard) 70
V.2.8Réponse de système de 2eme ordre avec PID en boucle fermée sous MATLAB (sans retard) 70
V.2.9Réponse de système du 2eme ordre avec PID en boucle fermée sous STEP7:(sans retard) 71
V.2.10Réponse de système du 2eme ordre avec PID en boucle fermée sou WINCC:(sans retard) 71
V.2.11Réponse de système du 2eme ordre avec PID en BF sous MATLAB (avec retard de 3s) 72
V.2.12Réponse de système du 2eme ordre avec PID en BF sous STEP7 (avec retard de 3s) 72
V.2.13Réponse de système du 2eme ordre avec PID en BF sous WINCC (avec retard de 3s) 73
V.2.14Réponse de système de 2eme ordre avec PID en BF sous MATLAB (avec retard de 3s) 73
V.2.15Réponse de système du 2eme ordre avec PID en BF sous STEP7 (avec retard de 3s) 74
V.2.16Réponse de système du 2eme ordre avec PID en BF sous WINCC (avec retard de 3s) 74
V.3- La réponse du système du 3éme ordre avec et sans retard 75
V.3.1Fonction de transfert 75
V.3.2Ajustement des gains de régulateur PI 75
V.3.3Réponse de système du 3ème ordre en BF sous MATLAB 75
V.3.4Réponse de système du 3ème ordre en BF sous WINCC 76
V.3.5Réponse de système du 3ème ordre en BF sous MATLAB (sans retard) 76
V.3.6Réponse de système du 3ème ordre en BF sous step7 (sans retard) 77
V.3.7Réponse de système du 3ème ordre en BF sous WINCC (sans retard) 77
V.3.8Réponse de système du 3ème ordre en BF sous MATLAB (avec retard de 2s) 78
V.3.9Réponse de système du 3ème ordre en BF sous STEP7 (avec retard de 2s) 78
V.3.10Réponse de système du 3ème ordre en BF sous WINCC (avec retard de 2s) 79
V.4- Conclusion 79
CHAPITRE VI : RESULTATS DE SIMULATION AVEC PI FLOU 80
VI.1- Système du 1er ordre sans retard 80
VI.1.1Réponse du système du 1er ordre sans retard sous Matlab 80
VI.1.2Réponse du système du 1er ordre sous WINCC 80
VI.2- Système du 1er ordre avec retard de 2s 81
VI.2.1Réponse du système du 1er ordre sous MATLAB 81
VI.2.2Réponse du système du 1er ordre avec retard sous WINCC 81
VI.3Système du 2eme ordre sans retard 82
VI.3.1Réponse du système du 2eme sans retard sous MATLAB 82
VI.3.2Réponse du système du 2eme ordre sans retard sous WINCC 83
VI.4Système du 2eme ordre avec retard 83
VI.4.1Réponse du système du 2eme ordre avec retard sous MATLAB 83
VI.4.2Réponse du système du 2eme ordre avec retard sous WINCC 84
VI.5Système du 3eme ordre sans retard 84
VI.5.1Réponse du système du 3eme ordre sous MATLAB 84
VI.5.2Réponse du système du 3eme ordre sous WINCC 85
VI.6Système du 3eme ordre avec retard de 2s 86
VI.6.1Réponse du système du 3eme ordre sous MATLAB 86
VI.6.2Réponse du système du 3eme ordre sous WINCC 86
VI.7Conclusion 86
Conclusion générale 87
Annexe 89
Bibliographie 90