La logique floue et la combinaison des règles et défuzzification
Chapitre II : Logique floue
II.1- Introduction à la logique floue
L’esprit humain manipule essentiellement des notions qualitatives lorsqu’il traite de l’information, et n’utilise le quantitatif qu’en deuxième ressort pour améliorer ce traitement d’information. Il manipule si mal par lui-même le quantitatif qu’il a besoin d’un support matériel pour le traiter : papier-crayon, calculateur…
Cette manipulation de notions qualitatives donne d’étonnants résultats : un individu se contente pour conduire un véhicule de notions vagues du genre « aller plus vite », «braquer un peu », etc. De la même façon, on dira qu’il fait très froid, froid, chaud ou très chaud, sans y faire correspondre une température précise.
La logique ou la commande floue a pour objet la manipulation par la machine de notions imprécises. Il fournit une méthodologie rigoureuse pour la mise en œuvre de raisonnements qui, en fait, se sentent familiers. La logique floue a été introduite en 1965 par L.A. Zadeh.
Ses principes ont été appliqués en 1974 par E.H. Mamdani à la construction d’un premier contrôleur flou. Aujourd’hui, plusieurs constructeurs et d’automates proposent des algorithmes de commande floue.
II.2- Commande floue d’un procédé
Depuis quelques années déjà, on trouve sur le marché des appareils de grande consommation (appareils de photos, vidéo, …) qui sont présentés comme faisant intervenir un réglage par logique floue ou « fuzzy-logic » ou encore « fuzzy-control ».
Au-delà de l’argument publicitaire évident, il est intéressant de comprendre ce nouveau concept de réglage, et de l’appliquer à certains types de problèmes de réglage rencontrés par l’ingénieur.
Le principe du réglage par logique floue part du constat suivant: dans les problèmes de régulation auxquels il est confronté, l’homme ne suit pas, à l’image de ses inventions, un modèle mathématique fait de valeurs numériques et d’équations.
Au contraire il utilise des termes tel que « un peu trop chaud, aller beaucoup plus vite, freiner à fond, etc… » ainsi que ses propres connaissances qu’il a dans le domaine. Ces connaissances sont, le plus souvent, acquises de façon empirique.
Le principe du réglage par la logique floue s’approche de la démarche humaine dans le sens que les variables traitées ne sont pas des variables logiques (au sens de la logique binaire par exemple) mais des variables linguistiques, proches du langage humain de tous les jours.
De plus, ces variables linguistiques sont traitées à l’aide de règles qui font référence à une certaine connaissance du comportement du système à régler. Sur la base de ce principe, différentes réalisations ont vu le jour et, actuellement, on trouve deux types d’approches pour le réglage par logique floue.
Dans l’une de ces approches, les règles sont appliquées aux variables à l’aide d’une approche numérique par le biais d’un microprocesseur spécialisé ou non ou d’un ordinateur.
Dans l’autre approche, les règles sont appliquées aux variables de façon analogique. Ces deux approches permettent de développer des organes de contrôle par le flou que l’on désigne par processeur digital flou ou par processeur analogique flou.
II.3-Principe de la logique floue
II.3.1-Introduction
La logique floue est une branche des mathématiques et, à ce titre, toute une série de notions fondamentales sont développées. Ces notions permettent de justifier et de démontrer certains principes de base. Dans ce qui suit, on ne retiendra que les éléments indispensables à la compréhension du principe du réglage par la logique floue.
II.3.2-Variables floues
Contrairement aux variables binaires qui sont définies par les deux états « vrai » ou « faux », les variables floues présentent toute une gradation entre la valeur « vrai» et la valeur « faux ».
L’exemple qui suit permettre de mieux saisir la distinction qui existe entre les variables binaires et les variables floues :
-Si l’on désire classer un groupe d’individu par leur taille en définissant la catégorie des petits par une taille en dessous de 160 cm, la catégorie des moyens par une taille comprise entre 160 cm et 180 cm et la catégorie des grand par une taille supérieure à 180 cm, la logique binaire donne la représentation de la pour les trois variables « petit », « moyen » et «grand ».
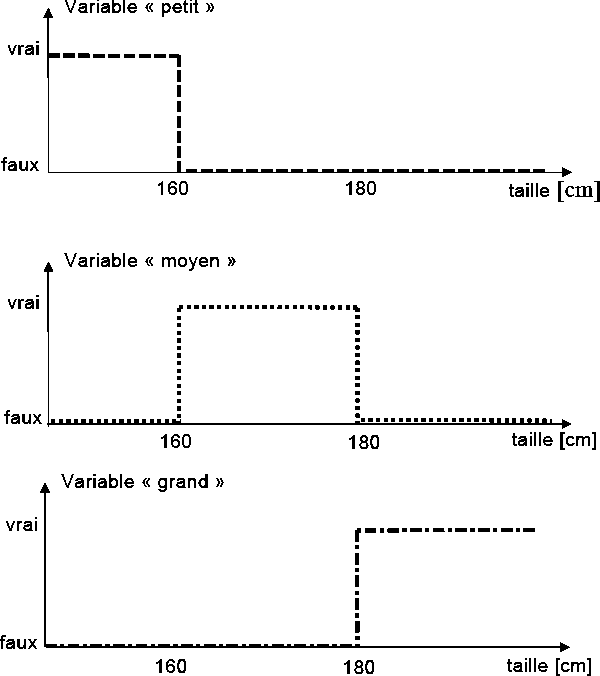
Fig.II.1 Représentation de la logique binaire pour les trois variables
Deux remarques s’imposent au sujet de cette représentation :
D’une part, on préfère représenter l’état de la variable à l’aide de son degré de vérité, en associant la valeur 1 (degré de vérité de 100%) à la valeur « vrai » et le degré de vérité nul à la valeur « faux ».
D’autre part, on constate que cette façon de faire, est très éloignée de ce que fait l’être humain lorsqu’il résout ce genre de problème. En effet, l’homme ne fait pas naturellement une distinction franche entre « petit » et « moyen » par exemple. Il utilise des expressions du genre « plutôt petit » pour qualifier une taille légèrement inférieure à 160 cm et « plutôt moyen » pour une taille légèrement supérieure à cette valeur.
En conclusion, la logique binaire présente l’avantage de la simplicité mais elle est assez éloignée de la logique utilisée naturellement par l’être humain.
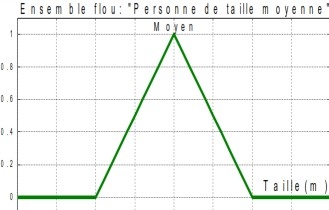
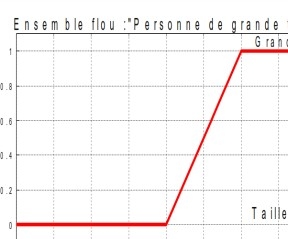
Si l’on représente le même problème à l’aide de la logique floue, les variables ne sont plus binaires mais présentent une infinité de valeurs possible entre le « vrai» et le « Faux ».
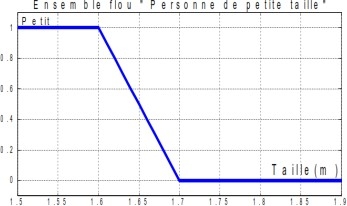 |
Fig.II.2 Représentation en logique Flou
On constate que cette représentation est beaucoup plus proche de la façon dont l’être humain raisonne puisqu’elle permet de faire intervenir des notions telles que « plutôt petit », « assez grand »… Cet avantage se fait, évidemment, au détriment de la simplicité de la représentation.
II.3.3-Règles d’inférence
On appelle règles d’inférence, l’ensemble des différentes règles reliant les variables floues d’entrée d’un système aux variables floues de sortie de ce système. Ces règles se présentent sous la forme :
Si condition 1 et/ou condition 2 (et/ou…) alors action sur les sorties.
L’exemple suivant, tiré de la vie quotidienne, permet d’illustrer ceci :
– Lorsque l’on prend une douche, un des problèmes qui se présente est de régler la température de l’eau. La variable d’entrée du système homme-douche est la température de l’eau mesurée à l’aide de nos capteurs de température.
Les variables de sorties sont les deux robinets eau chaude et eau froide. Dans la pratique, le réglage de la température se fait en utilisant notre expérience, expérience qui recouvre à la fois nos préférences et notre connaissance de l’installation sanitaire utilisée. Ce réglage se fait en utilisant des règles du genre :
- Si la température est très froide alors ouvrir à fond l’eau chaude
- Si la température est un peu trop froide alors fermé un peu l’eau froide
- Si la température est bonne alors laisser les deux robinets dans leur état.
- Si la température est trop chaude alors fermer un peu l’eau chaude et ouvrir un peu l’eau froide.
En termes d’intelligence artificielle, ces règles résument en fait l’expérience de l’expert et elles ne sont en général pas définissables de façon unique puisque chaque individu crée ses propres règles.
II.3.4-Fonctions d’appartenance
Il s’agit d’établir une relation entre le degré de vérité de la variable floue et la grandeur d’entrée correspondante, on parle de fuzzification :
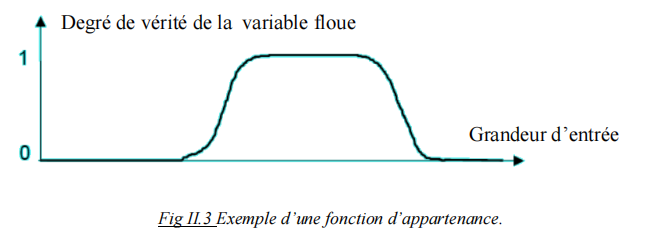
On peut évidemment choisir n’importe quelle forme pour les fonctions d’appartenance. Cependant, en pratique, on utilise les formes trapézoïdales.
II.4 -Combinaison des règles et défuzzification
L’ensemble des règles se présente sous la forme d’une énumération du type :
- Si condition 1 et/ou condition 2 (et/ou…) alors action sur les sorties
- Si condition 3 et/ou condition 4 (et/ou…) alors action sur les sorties
- Si condition 5 et/ou condition 6 (et/ou…) alors action sur les sorties
- …
La combinaison de ces différentes règles se fait à l’aide de l’opérateur ou. La justification du choix de l’opérateur se fond sur la pratique du langage courant : en effet, une telle énumération est comprise dans le sens
Si… alors… ou
Si… alors…ou
…
Bien que l’opérateur ou ne soit pas explicitement mentionné.
II.4.1-Défuzzification
Les valeurs obtenues lors de la combinaison des règles appliquées aux intervalles flous de la variable de sortie, définies une fonction d’appartenance.
Il s’agit de convertir cette information en une grandeur physique. Plusieurs façons de faire, peuvent être envisagées mais, en pratique, on utilise surtout les deux méthodes suivantes :
- Défuzzification par calcul du centre de gravité.
- Défuzzification par calcul du maximum.
En général, c’est la défuzzification par calcul du centre de gravité qui est la plus utilisée.
II.4.2-Défuzzification par calcul du centre de gravité
Il s’agit de calculer le centre de gravité de la fonction d’appartenance de la variable de sortie.
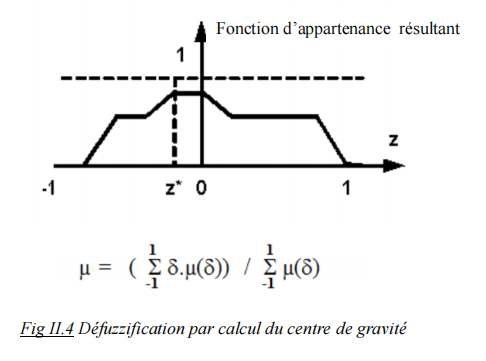
Le calcul du centre de gravité permet bien d’obtenir une seule valeur pour la grandeur de sortie. Son calcul est cependant relativement complexe puisqu’il nécessite le calcul d’une intégrale, ou dans le cas simple de fonctions d’appartenance en raies, d’une somme pondérée.
II.5-Régulateurs flous de type Mamdani
Dans les modèles linguistiques, appelés aussi modèle flous de type Mamdani, les antécédents et les conséquences des règles sont des propositions floues. La forme générale des règles de Mamdani est :
Un système flou de type Mamdani est basé sur une collection de règles du type :
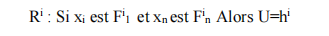
Où les xi représentent les variables d’entrées du régulateur et U est la variable de sortie de régulateurs, Fi étant les sous-ensembles flous.
Généralement les régulateurs flous de type Mamdani, sont des régulateurs à deux entrées, l’erreur et sa variation. Et une sortie, qui représente la variation de la commande, régie par des règles de la forme suivante :
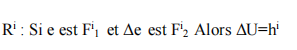
La structure du processus ainsi commandé est donnée par la figure II.5 qui correspond à un régulateur PI-flou.
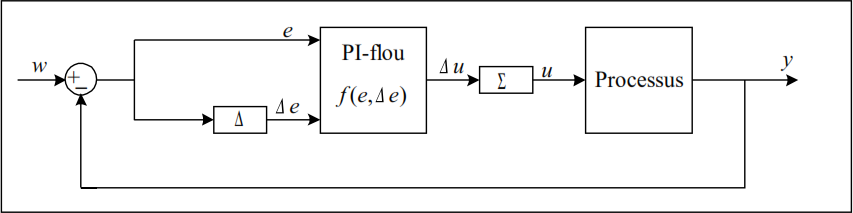
Fig.II.5 Structure d’un PI flou de type Mamdani.
La loi de commande du régulateur PD-flou, est obtenu en suppriment l’intégration à la sortie. Les règles ont la forme suivante :
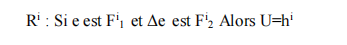
Pour le régulateur PID-floue, la loi de commande est obtenue grâce à l’erreur, sa variation et sa variation seconde. Les règles ont la forme suivante :
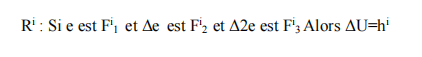
La défuzzification est généralement effectuée par la méthode du centre de gravité. Une variante de la méthode de Mamdani consiste à remplacer l’opérateur min de l’influence floue par l’opérateur prod (produit).
II.6-Régulateurs flous de type Sugeno
Le modèle de Sugeno est connu sous le nom de TSK, car il a été proposé par Takagi, Sugeno et Kang en 1988.ce modèle a pour but de donner à la sortie de la règle des valeurs concrètes, et non pas une valeur floue, qui nécessite une étape de défuzzification.
Le système flou de type Takagi-Sugeno, utilise des règles écrites de la manière suivante :
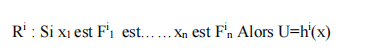
Chacune de ces règles représente un modèle local sur une région floue d’entrée, ou sur un sous- espace d’entrée. Dans chaque région, le modèle flou est défini par la fonction hi qui relie les entrées à la sortie numérique. Le modèle global est constitué par l’interpolation des modèles locaux.
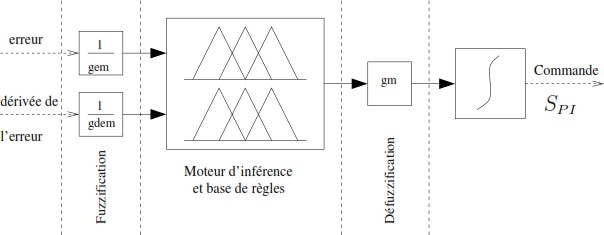
Fig II.6 Régulateur PI
II.7-Régulateurs floues de type PD et PI
Un régulateur flou PD (Proportionnel Dérivé) diffère d’un régulateur PI (Proportionnel Intégral) par l’utilisation qui est faite de leur sortie notée f(u). Un régulateur flou de type PD utilise sa sortie f(u) directement en termes de commande, selon la formulation:
Commande(t)=f(u).
La sortie d’un régulateur de type PI (Proportionnel Intégrale) est dans ce cas « Intégrée » (terme intégration dans PI) et nécessite le choix d’un pas de commande Δt pour la mise a jour de la position de l’actionneur. Le calcul de la commande se traduit par la formulation suivante:
Commande(t)=commande(t-Δt) +f(u).
Où:
- Commande(t): position de l’actionneur au temps t.
- f(u) est la sortie calculée par le régulateur flou.
- Δt est le pas de commande (ou de contrôle).
II.8- Avantage et inconvénients de régulateur PID et floue
On peut comparer dans le tableau ci-dessous le comportement des deux régulateurs PID et Floue dans les différents situations :
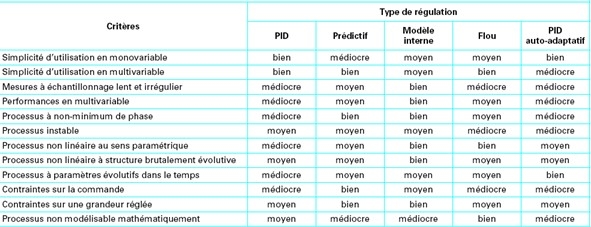
Fig.II.7 Comparatif des différents critères des régulateurs PID et Floue
II.9-Conclusion
Le choix de régulateur reste la clé de réussite de la régulation industrielle, un bon réglage d’une boucle de régulation est celui qui répondra au cahier des charges.
Enfin, nous avons touché la logique floue à travers les régulateurs de type Mamdani et de Sugeno. Nous présenterons ensuite dans le chapitre suivant le progiciel step7 et l’automate programmable s7-300.