Le contrôleur PID du quadrotor
Le contrôleur PID
Le contrôle par PID est la méthode la plus simple à programmer sur un processeur et elle est souvent employée pour les asservissements [16].
Cette méthode est basée sur une structure qui délivre un signal de commande à partir de l’erreur existante entre la référence et la mesure de son intégrale et de sa dérivée Figure 3.28.
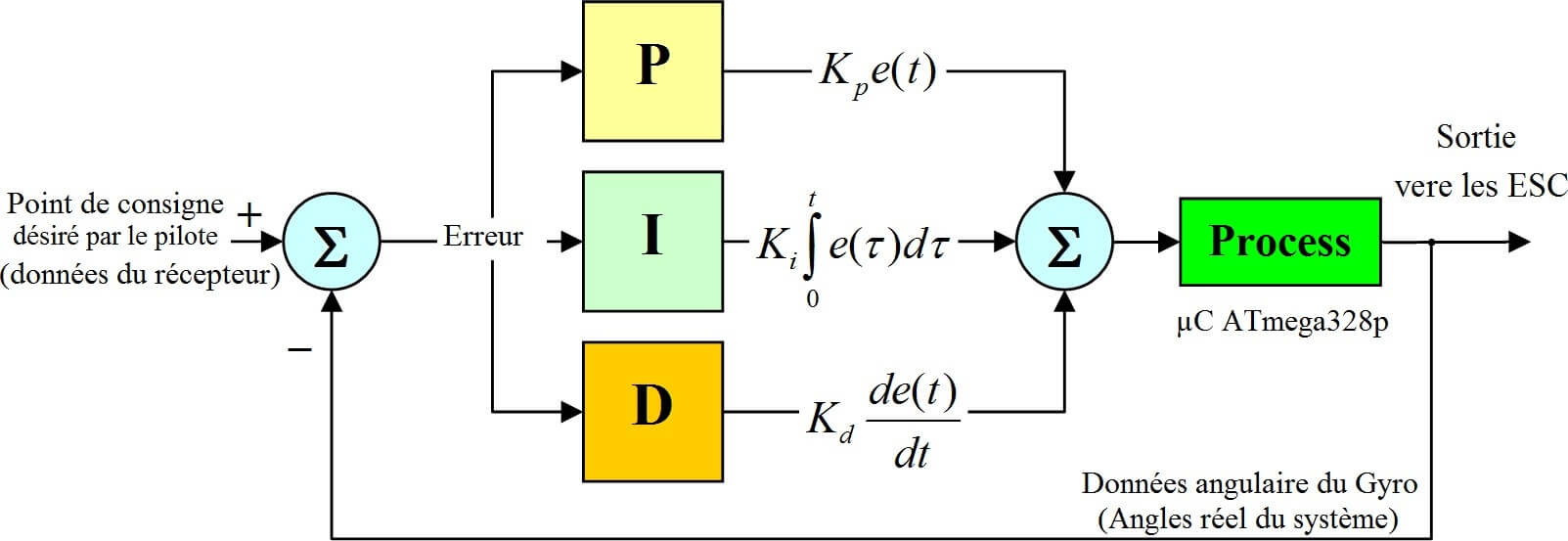
Figure 3.28 : Schéma de la boucle de contrôleur PID.
Le contrôle par PID est souvent utiliser dans l’industrie car il est très simple à mettre en place et s’avère efficace à réduire les erreurs pour la plupart des systèmes réels non linéaires.
Dans notre cas le principe de base du contrôleur PID est simple, lorsque le drone se trouve déséquilibré à cause du vent ou de la turbulence.
L’algorithme envoie une commande vers les ESC qui provoque une réaction dont le sens est opposé à celui qui a conduit au déséquilibre, afin que le drone retrouve l’état souhaité.
Plus précisément, il faut garder les valeurs mesurées du Gyro (données angulaires réel du système) identique au point de consigne désiré par le pilote (données d’entrée du récepteur de la routine d’interruption) Figure 3.29.

Figure 3.29 : Schéma montre le principe du PID utilisé dans ce contrôleur de vol.
Par exemple si le pilote ne veut aucun mouvement, le taux angulaire Gyro doit être également nul, donc l’erreur du système « 𝜀𝜀 » pour un axe de mouvement est la différence :
𝜀𝜀 = (Données d’entrée du Gyro − Données d’entrées du récepteur).
Le contrôleur PID calcule les corrections nécessaires pour les trois axes (Pitch, Roll et Yaw).
Les consignes pour le contrôleur PID sont les signaux d’entrée du récepteur et les variables des mouvements angulaires mesurées par le gyroscope.
Les sorties du contrôleur PID sont destinées pour contrôler la vitesse des moteurs du quadrotor afin d’assurer l’équilibre.
L’utilisation des opérateurs mathématiques (Proportionnel, Intégrateur et Dérivateur) permet de produire une sortie de commande adéquate pour le système.
Le modèle mathématique du contrôleur PID est décrit comme suit:
(𝑅𝑅) : L’erreur du système.
(𝑅𝑅) : Variable de sortie du PID.
𝐾𝐾𝑝𝑝 : Gain proportionnel.
𝐾𝐾𝑖𝑖 : Gain d’intégration.
𝐾𝐾𝑑𝑑 : Gain de dérivation.
Effet proportionnel 𝑲𝑲(𝒇𝒇)
Ce terme est proportionnel à l’erreur, il contribue à la stabilité et à la réactivité et permet une augmentation du temps de réponse du système, en fait le contrôleur seul n’est pas tout à fait suffisant pour stabiliser le drone [17].
Effet d’intégral 𝑲𝑲𝒇𝒇 (𝝉𝝉)𝝉𝝉 : Ce terme est proportionnel à l’intégrale de l’erreur, il permet au
𝒊𝒊 ∫𝟎𝟎 système d’atteindre le point de consigne désiré, permet aussi d’éliminé l’erreur statique du système et de diminuer l’impact des perturbations [17], il en résulte un système précis.
Effet de la dérivée 
Ce terme est proportionnel à la dérivée de l’erreur, il permet d’accéléré la réponse du système et d’éliminé les oscillations autours du point de consigne [17].
Saturation du contrôleur PID et choix des gains
Pour empêcher le PID de devenir incontrôlable, il est nécessaire de limiter la sortie PID à une valeur critique qui est le point de saturation du système et ça se détermine selon les caractéristiques du système et l’algorithme du contrôleur PID utilisé.
Cette limitation est souvent appliquée pour la sortie globale du contrôleur PID.
Chaque quadrotor est caractérisé par ces propres gains PID, généralement les gains PID varis d’un drone à l’autre en fonction du poids et du hardware utilisé.
La mise en œuvre de la commande PID exige d’abord une sélection adéquate des gains , 𝐾𝐾𝑖𝑖 et 𝐾𝐾𝑑𝑑 car la réponse de la sortie PID sera influencée en agissant sur ces trois gains.
Pour notre système les gains seront déterminés expérimentalement.
Algorithme PID du contrôleur de vol
Dans le programme du contrôleur de vol, trois contrôleurs PID sont utilisés pour les trois axes de mouvement essentiels (Pitch, Roll et Yaw).
Au début, il est nécessaire de transférer les variables des canaux d’entrée du récepteur (de la routine d’interruption) en degrés / seconde pour avoir les trois points de consigne de mouvement, identiques en grandeurs que les données d’entrée du Gyro.
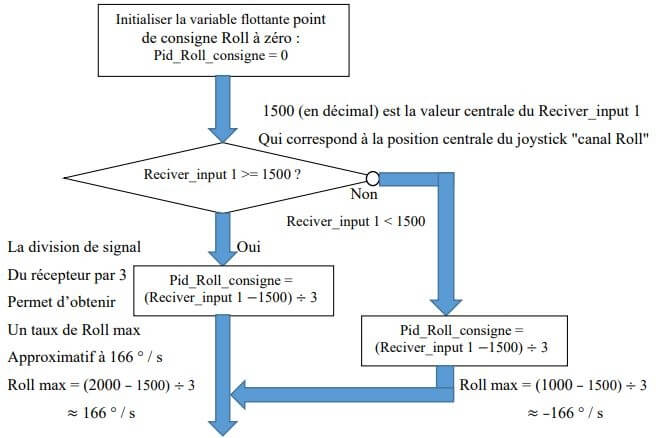
L’organigramme suivant explique l’étape de conversion des variables du récepteur en degrés / seconde pour un axe de mouvement « Roll », la même routine se répète pour les deux autres axes «Pitch et Yaw ».
Les entrées du contrôleur PID {données du récepteur : (Pid_Roll_consigne, Pid_Pitch_consigne, Pid_Yaw_consigne) et les données angulaires du Gyro :
(angle_roll, angle_pitch, angle_yaw)} sont connues, reste à déterminer les variables de sortie PID pour les mouvements (Pitch, Roll et Yaw).
Dans le sous-programme PID les trois parties (proportionnel, intégral et dérivé) sont calculées simultanément et combinées à un seul signal de sortie pour chaque axe de mouvement Figure 3.30.
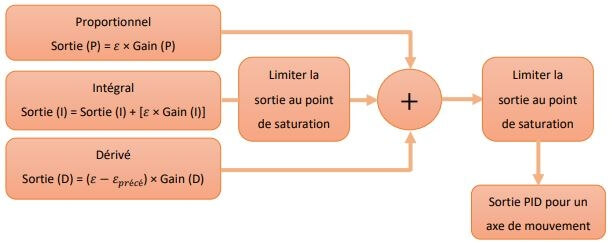
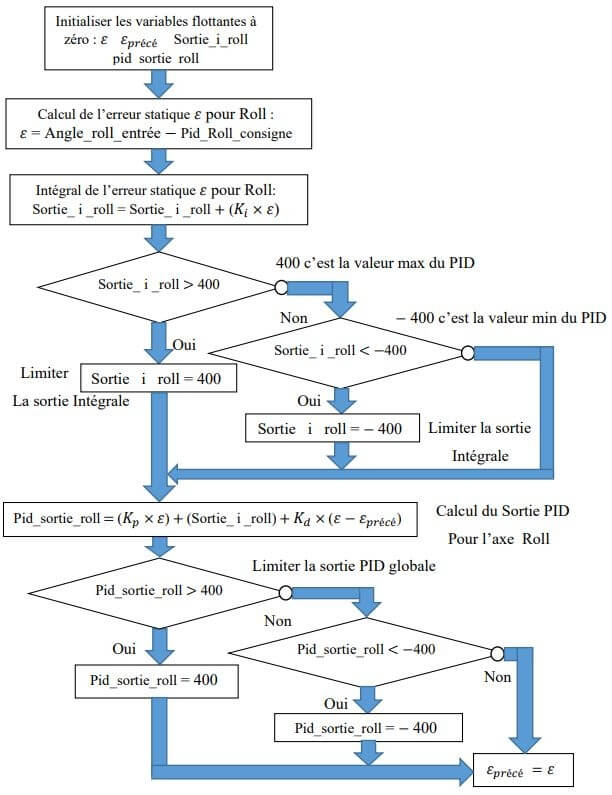
Figure 3.30 : L’algorithme utilisé dans le sous-programme PID du contrôleur de vol pour un axe de mouvement.
Sous-programme de sortie PID
L’organigramme suivant explique le calcul du sorties PID pour un axe de mouvement « Roll ».
La même routine se répète dans le sous-programme PID du contrôleur de vol pour les deux autres axes «Pitch et Yaw ».
𝜺𝜺𝒑𝒑𝒑𝒑é𝒄𝒄é = 𝜺𝜺L’erreur actuelle 𝜀𝜀 devienne l’erreur précédente 𝜀𝜀𝑝𝑝𝑟𝑟é𝑐𝑐é Pour le prochain calcule.
Contrôle des ESC
Dans cette partie, le but est de générer les impulsions de commande à envoyer pour les quatre ESCs en fonction des variables de sorties PID, afin de contrôler la vitesse des moteurs du quadrotor.
Les ESC sont connectés à l’Arduino Uno du contrôleur de vol via les broches digitales (D4, D5, D6 et D7) du registre PORTD.
Au début du programme principal, ces broches numériques doivent être déclarés en tant que sorties.
Après avoir calculé les variables de sortie du contrôleur PID pour les axes de commande (Pitch, Roll et Yaw), il devient possible de calculer les largeurs d’impulsion à fournir pour les ESC toutes les 4 ms afin de corriger la position du quadrotor.
Au début, il est nécessaire de déclarer le signal d’entrée du récepteur Throttle « Reciver_input 3 » comme la variable de base d’accélération.
Pour assurer que les trois contrôleurs PID ont suffisamment d’espace pour corriger le quadrotor à pleine vitesse, la variable d’accélération est limitée à 1800 μs au lieu de 2000 μs.
De cette façon, chaque contrôleur PID peut ajouter 200 μs supplémentaires en cas de besoin.
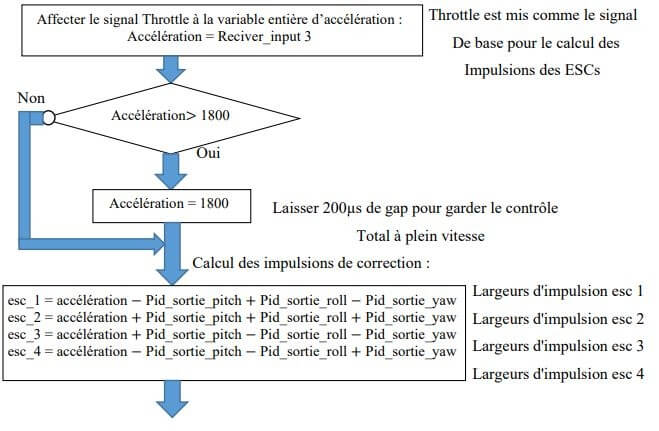
Pour calculer les impulsions des ESC, il suffit de combiner les variables de sorties PID séparées (Pitch, Roll et Yaw) et de les ajouter ou les soustraire à la variable d’accélération suivant cet algorithme :
Affecter le signal Throttle à la variable entière d’accélération : Accélération = Reciver_input 3
La Figure3.31 représente les axes Roll, Pitch et Yaw du quadrotor, la correction des impulsions des ESCs se fait selon les quatre instructions de l’algorithme citées en haut.
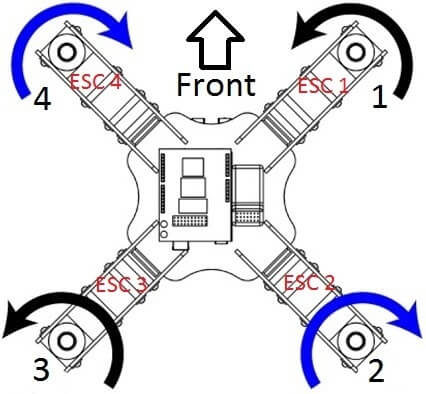
Figure 3.31 : Disposition des ESCs et direction de rotation du quadrotor
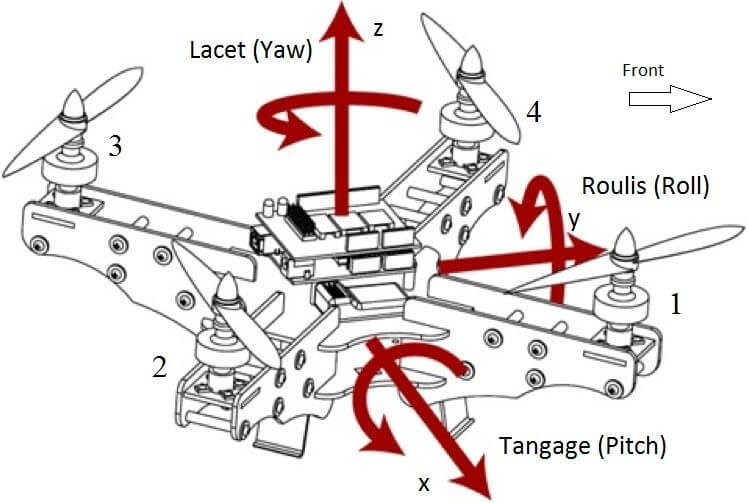
Figure 3.31 : Disposition des ESCs et direction de rotation du quadrotor
Pour l’axe de Roulis, si le quadrotor penche vers la droite en raison du vent ou de la turbulence, cela conduit le Gyro d’envoyer un angle de roulis positif (Données d’entrée Roll du Gyro> 0).
Lorsque le pilote ne veut aucun mouvement (le joystick de l’émetteur est en position centrale).
C’est à dire la variable roulis du récepteur est de 0 ° / sec (Pid_Roll_consigne= 0°) implique que la sortie roulis du contrôleur PID est positive (Pid_sortie_roll> 0) car l’erreur𝜀𝜀 > 0.
Donc pour que le quadrotor puisse revient à l’état stable 0°, la vitesse du moteur avant droit doit augmenter et ceci est fait en ajoutant la sortie du contrôleur PID Roll (Pid_sortie_roll) à l’impulsion de l’ESC 1.
Le même principe pour le tangage (Pitch), lorsque le front du drone est incliné en bas à cause d’une perturbation ou du vent, le Gyro envoie un angle de tangage négatif et la sortie du contrôleur PID Pitch devienne négative (Pid_sortie_pitch< 0).
En soustrayant la sortie du PID Pitch de l’impulsion ESC 1 implique que la vitesse du moteur1 s’augmente et le quadrotor retrouve l’état stable 0°.
Cela est illustré dans la Figure 3.32 et la Figure 3.33 pour l’axe de roulis (Roll) et la même chose pour le tangage (Pitch).
Le même principe se répète pour chaque combinaison moteur / ESC.

Figure 3.32 : L’algorithme du PID conduit le quadrotor de revenir À l’état voulu en agissant sur les ESCs

Figure 3.33 : Retour à l’état de consigne désiré par le pilote 0°.
Selon les dernières instructions citées dans l’algorithme en haut :
Si la sortie PID Yaw est (+) : les impulsionset
L’étape suivante consiste à envoyer les impulsions calculées aux ESC, ceci est fait en maintien les sorties numériques du PORTD (D4, D5, D6 et D7) à un niveau logique haut avec un délai de temps correspond aux largeurs d’impulsions ESC calculées précédemment.
Pour avoir le front descendant des impulsions, il suffit d’exécuter une boucle « while » jusqu’à ce que les quatre bits de poids fort du registre PORTD soient à zéro, ça signifie la fin de l’impulsion ESC.
Pour s’assurer que la fréquence des signaux PWM est de 250 Hz, un temporisateur de boucle vide est employé pour s’exécuter jusqu’à ce que les 4 ms soient expirées.
Finalement, il en résulte quatre trains d’impulsions PWM synchronisé avec une fréquence de 250 Hz, Figure3.34.
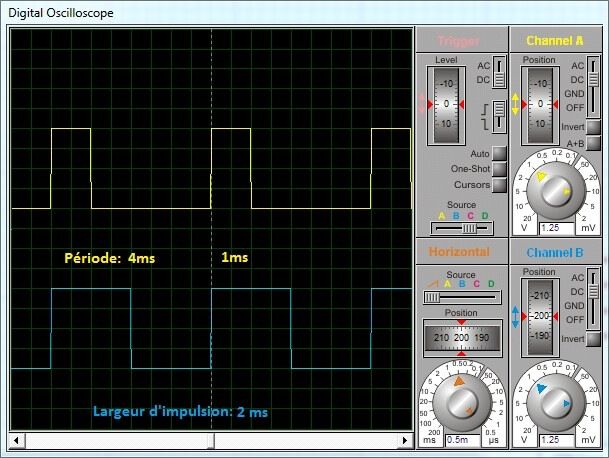
Figure 3.34 : Simulation des impulsions PWM de fréquence 250 Hz à envoyer pour deux ESCs
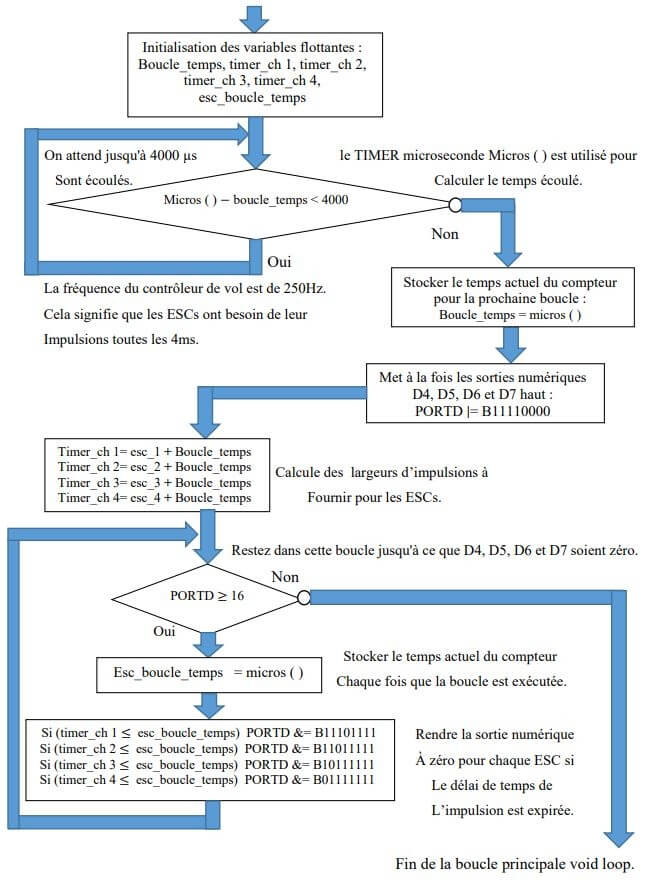
Toutes les données pour contrôler les moteurs sont disponibles. L’organigramme suivant explique l’algorithme utilisé pour générer des impulsions PWM aux ESC:
Initialisation des variables flottantes : Boucle_temps, timer_ch 1, timer_ch 2, timer_ch 3, timer_ch 4, esc_boucle_temps
Conclusion
Dans ce chapitre, les étapes de construction du quadrotor sont strictement illustré, le principe de fonctionnement du système et les instruments utilisés dans le hardware sont discutés, passant par la réalisation de l’émetteur et du récepteur puis le contrôleur de vol.
Le software utilisé en transmission et en réception est présenté avec détail et les diverses étapes de programme du contrôleur de vol sont expliquées.