Modélisation financière, simulation numérique et algorithme

Modélisation financière, simulation numérique et algorithme

I.3. Modélisation financière comme outil financier(13)

La modélisation financière consiste à représenter une situation financière grâce à un modèle mathématique, en fonction de différents paramètres.

La modélisation financière facilite ainsi la prise de décision, en permettant de simuler divers scénarios et d’aboutir à des recommandations.

La modélisation s’applique principalement à deux grands domaines de la finance, la finance d’entreprise et la finance de marché.

I.3.1 Finance d’entreprise

La modélisation financière a pris une place importante dans le domaine de la finance d’entreprise, de par le besoin des dirigeants de prévisions précises sur la situation financière future de leur entreprise, en fonction de différents paramètres, afin de pouvoir prendre les décisions adéquates.

Les applications comprennent :

• Évaluation d’entreprise (différentes méthodes d’évaluation sont en général modélisées)
• Construction d’un business plan
• Calcul d’indicateurs économiques (ex : coût des capitaux propres)

Les modèles sont principalement développés à partir d’états financiers comptables passés ainsi que d’hypothèses formulées pour le futur (exemples : taux de croissance du chiffre d’affaires, investissements futurs, évolution des coûts d’exploitation, etc.).

Ces hypothèses sont facilement modifiables afin de pouvoir simuler différents scénarios (par exemple optimiste, neutre et pessimiste) qui aideront dans la prise de décision.

Ces modèles sont le plus souvent réalisés à l’aide de logiciels tableurs avec accessoirement l’aide de langages de programmation (ex : Microsoft Excel et VBA).

I.3.2 Finance de marché

Dans ce domaine, la modélisation financière a pour but de simuler divers phénomènes de marché, dans le but d’aider à la gestion de portefeuilles d’actifs.

Les applications comprennent :

1. Modélisation du risque et de l’incertitude
2. Calcul du prix d’une option
3. Optimisation de portefeuille.

La modélisation financière des marchés implique le développement de modèles mathématiques complexes incluant des lois probabilistes.

Les paramètres numériques sont dans ce cas continus et les modèles nécessitent donc l’utilisation de méthodes avancées (séries et suites numériques, équations différentielles, méthode d’informatique, etc.).

(13) Paul MYERS (2015), Les qualités requises pour devenir un as de la modélisation Financière, DUNOD.

Dans le cas de la finance de marché, même si les tableurs sont utilisés, la modélisation s’appuie parfois sur des logiciels de programmation plus avancés, de par la complexité des modèles développés.

I.3.3 Un commentaire sur la compétition internationale de modélisation financière

Un signe de l’engouement actuel pour la modélisation financière, le championnat du monde de modélisation financière sur Excel Model Off a été organisé pour la première fois en 2012.

Sponsorisé par plusieurs entreprises prestigieuses, plus de 2000 participants ont alors concouru. La dernière édition a quant à elle réuni 4000 participants à Londres en décembre 2015.

Les candidats sont testés sur différentes compétences de modélisation financière, comme la capacité à construire des modèles mathématiques d’évaluation financières, la maitrise de l’informatique pour la manipulation des données et la capacité de produire les modelés de réflexions complexes adaptés à la demande de clients.

I.3.4 Catégories des modèles

I.3.4.1 Les Modèles prédictifs

Ces modèles mathématiques sont utilisés pour anticiper des événements ou des situations, comme prévoir le temps avec la météorologie, estimer les prix potentiels des actifs financiers avec les modèles d’évaluation en finance qu’on étudie dans ce processus, ou prévenir les épidémies.

On parle de modèles prédictifs, dans lesquels des variables connues, dites « explicatives », vont être utilisées pour déterminer des variables inconnues, dites « à expliquer », qui va du modèle vers le réel.

L’application des suites et des séries numériques.

I.3.4.2 Les Modèles descriptifs

Dans ce cas, les modèles servent à représenter des données historiques. On parle de modèles descriptifs. L’objectif est de rendre compte, de manière interprétable d’une masse d’informations.

L’archétype de ces modèles est la comptabilité : elle décrit de manière simplifiée les événements économiques réels en leur affectant un compte, c’est-à-dire une « étiquette » censée les caractériser.

Ces comptes sont ensuite agrégés pour présenter de manière standard la situation économique des entreprises et des pays, qui part du réel vers le modèle.

I.3.4.3 Classification

Les deux catégories de modèles sont parfaitement liés : une bonne prédiction suppose au moins la prédiction de la situation passée et actuelle, c’est-à-dire une bonne description.

Inversement, une bonne description serait parfaitement vaine si elle ne servait pas au moins de diagnostic, ou de carte, pour identifier la conduite à tenir.

Un même modèle mathématique peut se trouver applicable à de nombreuses situations, n’ayant pas forcément un rapport évident.

Par exemple, des générateurs de paysages sont capables de créer des formes réalistes d’objets aussi différents que des montagnes, des arbres, des rochers, de l’herbe, des coquillages, avec un seul modèle général, alors même que les processus de croissance et de constructions de ses objets sont très divers.

Si, au lieu de créer un nouveau modèle, on est capable de rapprocher un problème d’un ancien modèle connu, on obtient immédiatement une masse de données très utile.

Une grande partie du travail est donc de reconnaître qu’un modèle connu s’applique, ou à étendre les propriétés connues d’une classe particulièrement utile de modèle (propriété qu’on pourra ensuite utiliser plus largement).

I.4. Simulation numérique comme outil financier

La simulation informatique ou numérique désigne l’exécution d’un programme informatique sur un ordinateur ou réseau en vue de simuler un phénomène physique réel et complexe.
(par exemple : chute d’un corps sur un support mou, résistance d’une plateforme pétrolière à la houle, fatigue d’un matériau sous sollicitation vibratoire, usure d’un roulement à billes…).

Les simulations numériques scientifiques reposent sur la mise en œuvre de modèles théoriques utilisant souvent la technique des éléments finis.

Elles sont donc une adaptation aux moyens numériques de la modélisation mathématique, et servent à étudier le fonctionnement et les propriétés d’un système modélisé ainsi qu’à en prédire son évolution.

On parle également de calcul numérique. Les interfaces graphiques permettent la visualisation des résultats des calculs par des images de synthèse.

Ces simulations informatiques sont rapidement devenues incontournables pour la modélisation des systèmes naturels en physique, chimie, biologie et ressèment en finance mais également des systèmes humains en économie et en science sociale.

Elles permettent de limiter le risque et d’éviter le coût d’une série d’épreuves réelles et elles peuvent offrir un aperçu sur le développement d’un système trop complexe pour simuler avec de simples formules mathématiques.

La simulation numérique est utilisée pour :

• prévoir l’état final d’un système connaissant son état initial (problème direct);
• déterminer les paramètres d’un système connaissant un ou plusieurs couples (état initial – état final) (problème inverse);
• préparer des opérateurs à des conditions plus ou moins rares dans leur interaction avec un système complexe (simulation d’entraînement).

I.4.1 Critique étymologique

La simulation numérique ne doit évidemment pas être confondue – comme le terme de simulation le suggère – avec le réel.

Ce n’est pas parce que l’ordinateur dit que cela va se passer comme cela que cela se comporte effectivement comme tel dans la réalité (par exemple : simulations numériques des prévisions météorologiques).

La simulation numérique n’est qu’une représentation du problème réel assise sur le modèle mathématique.

Si le modèle mathématique ainsi informatisé est erroné, les résultats calculés sont alors faux et peuvent amener à des prises de décision erronées.

En particulier, un modèle est construit pour un usage donné, et son emploi dans un autre contexte à de fortes chances d’engendrer des résultats faux (voir validation des simulations).

La meilleure façon de résumer cette critique épistémologique est : « la carte n’est pas le territoire ! ». D’où la nécessité d’une adaptation précise lors de la modélisation et de la construction de l’algorithme.

I.4.2 Brève historique

La simulation numérique est apparue en même temps que l’informatique pour les besoins du projet Manhattan pendant la Seconde Guerre mondiale, afin de modéliser le processus de détonation nucléaire.

La première simulation numérique « civile » en physique théorique fut l’expérience de Fermi-Pasta-Ulam (1953). Depuis, elle a évolué parallèlement à l’informatique.

Depuis le début des années 80, l’introduction des mathématiques dans les pratiques financières a accompagné une modernisation profonde de tous les domaines de la finance.

Cette modernisation a favorisé les progrès de l’économie, d’investissement et des activités de marché.

Les économistes ne savent pas piloter, ni mesurer la montée des risques qui se développent à longueur du temps et cela entrainent les crises financières dont on parle partout dans le monde.

Voici la nécessité urgente d’adapter la modélisation financière à la simulation informatique, dont on parle aujourd’hui de la simulation financière (14).

14 PL.LIONS , (2014), Evaluation des modèles mathématiques en finance, Louis Bachelier, France.

I.4.3 Catégories de simulation informatique

On peut distinguer trois catégories de simulations :

La simulation continue, où le système se présente sous la forme d’équations mathématiques à résoudre. Elle permet de suppléer à la résolution analytique quand celle-ci est impossible.

Effectuée au départ sur des calculateurs analogiques, elle s’est effectuée aussi sur des ordinateurs et un troisième type de calculateurs qui n’a pas eu de lendemain, les calculateurs aléatoires.

La simulation discrète dans laquelle le système est soumis à une succession d’évènements qui le modifient. Ces simulations ont vocation à appliquer des principes simples à des systèmes de grande taille.

La simulation par agents, où la simulation est segmentée en différentes entités qui interagissent entre elles.

Elle est surtout utilisée dans les simulations économiques et sociales, où chaque agent représente un individu ou un groupe d’individus.

I.5. Notions d’algorithme

I.5.1 Définition

Un algorithme est une suite finie de règles à appliquer dans un ordre déterminé, à un nombre fini de données pour arriver à un résultat c’est-à-dire qu’un algorithme est une procédure de calcul bien définie qui prend en entrée un ensemble de valeurs et qui délivre en sortie un ensemble de valeurs résolvant un problème réel.

Données Machine résultats

Pour que la machine donne les résultats attendus en fonction des données fournies, il faut lui indiquer les actions à exécuter, c’est-à-dire comprendre le problème posé et indiquer les données fournies (input), Indiquer les résultats que l’on souhaite obtenir (output) et déterminer le processus qui permet d’obtenir les résultats à partir des données.

En simulation financière qu’on étudie, l’algorithme permet d’exécuter ou de simuler un ensemble de valeurs séquentiellement à longueur du temps d’un modèle mathématique conçu lors de la modélisation sans qu’on lui indique encore un autre ensemble de valeurs en temps réel.

Cette technique permet de représenter graphiquement une situation financière aléatoire.

L’algorithme doit avoir une structure bien définie. Cette structure doit comporter :

• L’en-tête qui comprend le nom de l’algorithme.
• Les déclarations des variables
• Le corps de l’algorithme qui contient les instructions.

Toutes les instructions doivent situer entre le mot Début et le mot Fin, et chaque instruction doit comporter un point-virgule à la fin.

I.5.2 Formuler un algorithme

Lors de la conception d’un algorithme, il est important de se focaliser sur la logique de résolution, sans être perturbé par les détails des langages de programmation.

Sur le problème de la recherche d’un partenaire pour travailler, voici deux façons usuelles de les décrire :

1. L’ordinogramme
2. Le pseudo-code

a. Ordinogramme

C’est la représentation schématique ou graphique de l’algorithme.

Nous utilisons les configurations suivantes :

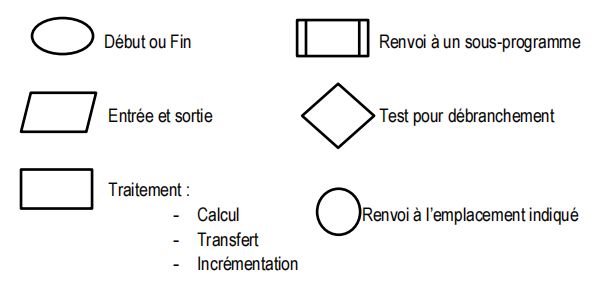
Début ou Fin
Renvoi à un sous-programme

Entrée et sortie
Test pour débranchement

Traitement :
Calcul
Transfert
Incrémentation

Renvoi à l’emplacement indiqué

b. Le pseudo-code ou langage algorithmique

Représentation textuelle d’un algorithme, dit aussi Langage de Description des Algorithmes (LDA en abrégé); c’est un langage formel et symbolique qui utilise:

• Des noms symboliques destinés à représenter les objets sur lesquels s’effectuent des actions.
• Des mots-clés et des opérateurs qui traduisent les opérations exécutables par un exécutant donné..

Exemple :

Algorithme lecture
Var i, j, n : entier
Tableau A [n, n] : réel
Début

Lire n

Pour i = 0 jusqu’à n

Pour j = 0 jusqu’à n

Ecrire («Entrer un élément de la ligne», i, » et colonne «, j)
Lire A [i, j]

j suivant

i suivant

Fin

I.5.3. Structures algorithmiques

On distingue la structure séquentielle, la structure conditionnelle et la structure itérative :

I.5.3.1 Structure séquentielle

La structure séquentielle est la plus simple car il y’a aucune condition et toutes les instructions s’exécutent de façon séquentielle.

Dans la finance quantitative qu’on étudie on peut faire allusion à l’application de suites ou séries numériques dans la recherche da valeurs futures « accumulation ou capitalisation » qu’on étudie spécifiquement.

Dans une structure séquentielle, les instructions sont exécutées l’une après l’autre et son ordinogramme se présente de manière suivante :

• Format général

Ecrire
Instruction 1
…………..
Instruction n
Afficher

Exemple :

Algorithme affectation
Var A, B, C, X : entier
Début

Ecrire («Entrer la valeur de A, B, C»)
Lire A, B, C
X A
A B
B C
C X

Ecrire (A, B, C)

Fin

I.5.3.2 Structure conditionnelle

La structure conditionnelle ou alternative est utilisée pour la résolution des problèmes ayant deux alternatives.

La structure conditionnelle est une situation dans laquelle on peut choisir que deux solutions possibles, comme le modèle de Black- Scholes.

• Format général

Si (condition) alors
Instruction 1
Si non
Instruction 2
Fin s

Si C alors

…………B1…………

Si non…………

B2…………

Fin Si………

I.5.3.3 Structure itérative

La structure itérative ou répétitive et/ou boucle permet la résolution des problèmes faisant appels à plusieurs choix possibles. Dans une boucle, le nombre de répétition peut être connu d’avance ou pas.

Si nombre de répétition n’est connu d’avance, on utilise un prédicat (une condition) pour mettre fin à la répétition. On distingue :

• La boucle « pour »
• La boucle « tant que ou répéter »

La boucle « pour » : on utilise la boucle pour lorsqu’on connait d’avance le nombre de répétition à effectuer, c’est-à-dire lorsqu’on connait le nombre de fois qu’on doit exécuter une action.

La boucle « tant que ou répéter » : on utilise la boucle tant que lorsqu’on ne connait pas d’avance le nombre de répétition à effectuer mais on connait une condition d’arrêt.

Exemple :

Algorithme lecture
Var i, j : entier
Tableau A [9,9] : Réel
Début

Pour i = 0 jusqu’à 8
Pour J = 0 jusqu’à 8

Lire A [i, j]

J suivant
I suivant

Fin