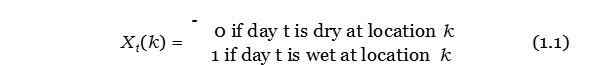Mohammed V University
Faculty of sciences Rabat
Department of mathematics master
of statistics and econometrics
Stochastic generation of daily, monthly, and annual precipitation
Author: Said OBAKRIM
Supervisor:
Prof. Abdelhak ZOGLAT
July 24, 2019
This work would not be possible without the guidance, assistance, and support of my supervisor Prof. Abdelhak Zoglat. I am very greatful for the opportunity to pursue my research interests under his supervision and consider it an honour to call myself one of his students.
I would like to extend a heartfelt thanks to all the other professors who teached me and helped me during this period of my master’s degree.
1.1 Single site stochastic generation of daily precipitation 6
1.1.1 Single site precipitation occurrence process. 6
1.1.2 Single site precipitation amounts process.7
1.2 Multisite stochastic generation of daily precipitation
1.2.1 Multisite precipitation occurrence process. 10
1.2.2 Multisite precipitation amounts process 12
2 Stochastic generation of monthly and annual precipitation 15
2.1 Single site monthly and annual models 15
2.1.1 Single site monthly model.15
2.1.2 Single site annual model 17
2.2 Multisite monthly and annual models 18
2.2.1 Multisite monthly model 18
2.2.2 Multisite annual model 20
3 Application 22
3.1 Data.22
3.2 Daily simulations 23
3.2.1 Daily occurrence process 23
3.2.2 Daily amounts process
3.3 Monthly simulations. 30
3.4 Annual simulations.33
4 Conclusion 38
A Maximum likelihood estimation of transition probabilities 40
B Simulation of multivariate normal distribution 42
C Implementation of the models in R 43
Meteorological data are commonly needed as inputs to hydrological and agricultural modeling systems. To evaluate these models, it is rarely sufficient to use only the observed weather data.
Not only because observed ground-based climate data are inadequate in terms of their length and completeness, but the use of observed sequences gives a solution based on only one realization of the weather process, hence it provides us with only one scenario.
To address this issue, it is beneficial to generate synthetic sequences of climate data based on the stochastic structure of the weather process. These statistical models are known as ”weather generators”.
Weather generators (WGs) are also used to construct climate change scenarios (Wilby, R.L, 1994). As the future climate data are not available, WGs can be used to simulate synthetic sequences of climate variables that represent the consequences of climate change, and to investigate changes in both mean climate and its variability.
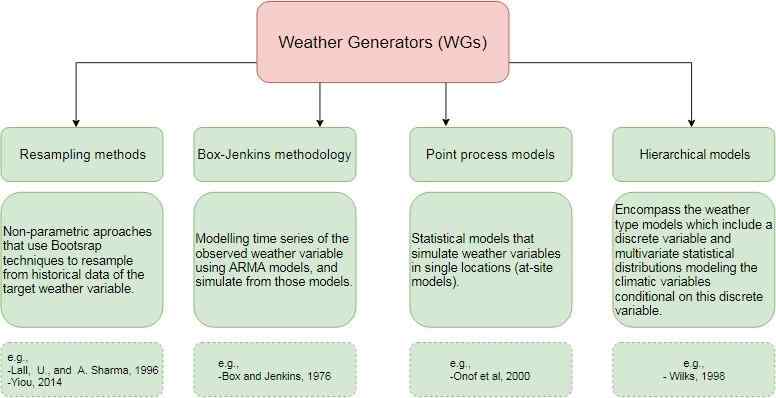
According to (Ailliot 2015), current WGs can be divided into four groups: resampling methods, Box-Jenkins methodology, point process models and hierarchical models, figure 1.
As rainfall processes are the most crucial variables in hydrological modelling systems, the most effort in the creation of weather generators has been dedicated to rainfall processes.
Precipitation is a mixed variable that contains both discrete and continuous sequences and is very often exactly zero. Thus, there is a strong discontinuity in the probability distribution of rainfall data between the zero and the nonzero observations. Therefore, most models contain separate treatments of the precipitation occurrence and amounts processes. The precipitation occurrence process generates the binary variable representing wet or dry days, and the precipitation amounts process simulates the nonzero observations.
This paper is organized as follows. Chapter 1 presents the single site and multisite stochastic generation of daily precipitation models. Chapter 2 presents the single site and multisite stochastic generation of monthly and annual precipitation models. And the last chapter presents the application of the models described in the two first chapters using daily rainfall data of 6 stations in Scotland.
Figure 1: Diagram for weather generators models
1 Stochastic generation of daily precipitation
1.1 Single site stochastic generation of daily precipitation
Denote Xt(k) the binary event of wet and dry day at location k
on day t such that
X (k) = . 0 if day t is dry at location k (1.1)
Here day t is classified as wet day if the precipitation amount is above some fixed threshold. Denote rt(k) the nonzero precipitation amounts at location k on day t.
Thus, the time series of precipitation amounts at location k is then
Yt(k) = Xt(k)rt(k) (1.2)
1.1.1 Single site precipitation occurrence process
Assuming that the probability of rainfall on any day depends only on whether the previous day was wet or dry, the precipitation occurrence is modeled using the first-order two-stage Markov process. The Markov process is defined by the transition probabilities p01(k) and p11(k) such that
p01(k) = P (Xt(k) = 1|Xt−1(k) = 0)
and
p11(k) = P (Xt(k) = 1|Xt−1(k) = 1), which will be estimated from the observed binary sequences of the precipitation occurrence process using maximum likelihood estimation (see Appendix A).
The other conditional probabilities are derived from these two transition probabilities by p00(k) = 1 − p01(k) and p10(k) = 1 − p11(k).
To simulate the Xt(k) series we first generate a uniform [0, 1] random number ut(k) for each day t and location k and the state of each day is determined using the transition probabilities p01(k) and p11(k). If the previous day (t − 1) was dry, then day t is simulated to be wet if ut(k) ≤ p01(k), and otherwise it is also dry. If the previous day was wet, then the current day is simulated to be wet if ut(k) ≤ p11(k), and is dry otherwise.
To summarize, let pc(k) be the critical probability such that
p (k) = . p01(k) if Xt−1 = 0
, (1.3)
the next value of the Xt(k) is determined as
X (k) = . 1 if ut(k) ≤ pc(k)
. (1.4)
1.1.2 Single site precipitation amounts process
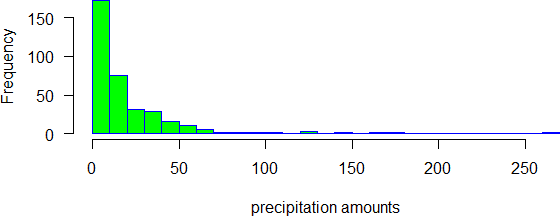
The precipitation amounts process simulates the nonzero sequences which are typically strongly skewed to the right, with many small values and few but important large precipitation amounts (Figure 1.1) that are most important to hydrological and agricultural models.
Figure 1.1: Histogram of daily precipitation amounts
Under the assumption that precipitation amounts on wet days are independent and follow the same distribution, a number of models have been proposed for the distribution of daily precipitation amounts given the occurrence of a wet day. The most common distributions are the exponential, gamma, and mixed exponential distribution.
Figure 1.2 illustrates the difference between the exponential and the gamma distributions fitted to nonzero rainfall amounts at a particular location. In this case, the gamma distribution is more co sistent compared to the exponential distribution (AIC for the gamma distribution is 2830.327 and for the exponential distribution 2841.764).
Having decided which distribution fits well the nonzero precipitation amounts, simulations are accomplished by generating uniform [0, 1] random variates and using the inversion theorem.
Figure 1.3 illustrates the single site two-part model consisting of the precipitation occurrences and amounts process.