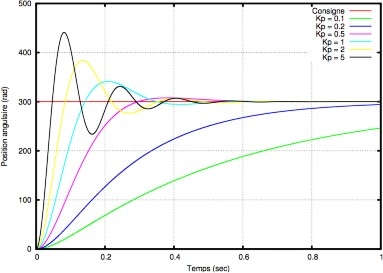
Régulation PID, qualités attendues et Type de régulateurs
I.5- Qualités attendues d’une régulation
Les qualités exigées les plus rencontrées industriellement sont la stabilité, la précision et la rapidité d’une grandeur à réguler.
I.5.1Stabilité
La qualité essentielle pour un système régulé, et donc exigée à tout prix, est la stabilité. En effet un système instable se caractérise soit par des oscillations d’amplitude de plus en plus grande de la grandeur observée soit par une croissance irréversible négative ou positive de la grandeur observée.
Dans les deux cas, l’objectif de la régulation n’est bien entendu pas atteint, mais surtout il y’a risque de détérioration physique du procédé et donc d’insécurité.
I.5.2Précision
I.5.2.1. Précision statique
Il est naturel d’évaluer la précision d’un système régulé en comparant l’objectif atteint par rapport à celui exigé. La précision d’un système régulé se mesure donc à l’écart entre la consigne demandée et la mesure en régime permanent ; on parle alors de précision statique. Plus l’écart statique est petit, plus le système est précis.
L’évaluation de la précision statique s’effectue en réalisant une variation rapide de consigne en amplitude et en mesurant la variation d’amplitude finalement obtenue de la mesure.
I.5.2.2. Précision dynamique
La précision dynamique est donc à prendre en compte lors des réglages des régulateurs. Elle s’évaluera généralement par le dépassement maximal que peut prendre la mesure par rapport à la consigne.
I.5.3Rapidité
La rapidité d’un système régulé s’évalue par le temps nécessaire à la mesure pour entrer dans une zone
± 5% de sa valeur finale (soit entre 95% et 105%).Le système régulé est d’autant plus rapide que le temps de réponse à 5% est court.
I.6- Régulation en boucle ouverte/ en boucle fermée
I.6.1 -En boucle ouverte
Pour une variation manuelle d’amplitude finie de la commande on a une variation de la grandeur à maîtriser ou à réguler.
La régulation en boucle ouverte ne peut être mise en œuvre que si l’on connait la loi régissant le fonctionnement du processus (autrement dit, il faut connaitre la corrélation entre la valeur mesurée et la grandeur réglante).
I.6.2-En boucle fermée
La grandeur réglante exerce une influence sur la grandeur réglée, pour la maintenir dans des limites définies malgré les perturbations.
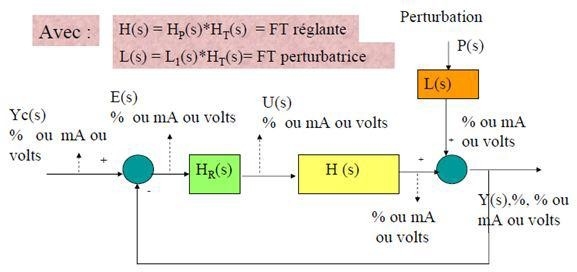
Fig.I.4 Schéma bloc ou fonctionnel d’un système en boucle fermée simplifié
On pose FTBO(s) =Hr(s).H(s).
On montre alors directement d’après les règles algébriques sur les schémas fonctionnels vues précédemment que :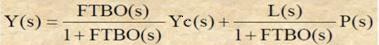
Ou encore :
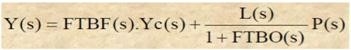
Avec :
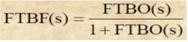
I.7-Régulation PID
En pratique, à une catégorie donnée de systèmes à asservir correspond un type de correcteur adopté. Pour effectuer un choix judicieux, il faut connaître les effets des différentes actions de régulateur PID : proportionnelle, intégrale et dérivée. Présenté sur le schéma :
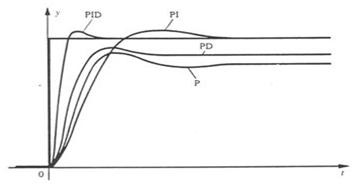
Fig.I.5 Action proportionnelle, intégrale, dérivée
I.7.1Régulateur proportionnel (Type P)
Dans le cas d’un régulateur P, la variable régulée est toujours proportionnelle à l’erreur calculée. Il en résulte qu’un régulateur P réagit sans temps de retard à tout écart entre la sortie et la consigne, et seul dans ce cas sera générée une valeur régulée y.
Le graphique suivant décrit le comportement d’un régulateur proportionnel :
Fig.I.6 Graphique d’un régulateur proportionnel
L’avantage de ce type de régulateur réside d’une part dans sa simplicité (la réalisation électronique se résume dans certains cas à une simple résistance) et d’autre part dans sa rapidité de réaction (par rapport à d’autres types de régulateur).
Le désavantage principal d’un régulateur proportionnel réside en la présence d’une erreur de régulation permanente.
En effet, la valeur de consigne ne sera, même à long terme, jamais complètement atteinte. Ce désavantage tout comme celui d’un temps de réaction non idéal ne se laissent qu’imparfaitement compenser par une augmentation du facteur de gain proportionnel, qui tend à rendre le système oscillant.
Un trop grand gain proportionnel engendre dans le pire des cas une oscillation permanente, la sortie s’éloignant périodiquement de la valeur de consigne.
Ce problème d’une erreur de régulation permanente peut être résolu avec un régulateur de type intégral.
I.7.2Régulateur intégral (type I)
Un régulateur de type intégral permet de complètement compenser une erreur de régulation constante tant que l’erreur n’est pas nulle, la valeur de la variable régulée est ajustée. La régulation se termine lorsque la sortie a atteint la valeur de la consigne ou que la variable régulée a atteint un seuil maximal fixé par les propriétés du système (Umax, Pmax …etc.).

La formulation mathématique de ce comportement intégral est : la variable régulée est proportionnelle à l’intégrale par rapport au temps de l’erreur.
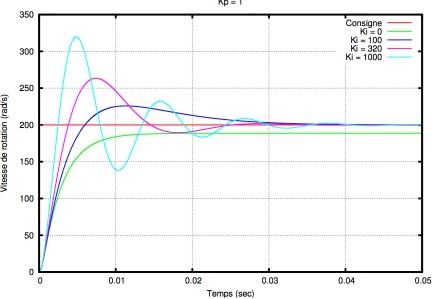
Fig.I.7 Régulateur I
La vitesse avec laquelle la variable régulée augmente (ou diminue) dépend de l’erreur de régulation et de la constante de temps d’intégration choisie.
I.7.3Régulateur de type PI
Le régulateur de type PI est l’un des plus utilisés dans la pratique. Il s’agit d’un couplage parallèle entre un régulateur proportionnel et un régulateur intégral.
S’il est correctement paramétré, le régulateur PI cumule les avantages des deux types de régulateurs (Stable, rapide, faible erreur résiduelle), tout en compensant leurs désavantages respectifs.
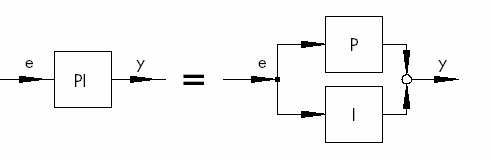
Fig.I.8 Régulateur de type PI
Le comportement dans le temps est caractérisé par le facteur proportionnel Kp et la constante d’intégration Ti. Grâce à la partie proportionnelle, le régulateur réagit immédiatement à toute erreur de régulation e, alors que la partie intégrale ne fera effet qu’après un certain temps.
La constante d’intégration Ti est le temps qu’il faut à la partie I pour avoir la même amplitude que prend la partie P de façon instantanée. Si l’on veut renforcer la partie intégrale, il faut comme pour un régulateur intégral réduire la constante Ti.
I.7.4Régulateur dérivée (type D)
Le régulateur dérivé établit une valeur régulée en fonction de la vitesse de variation de l’erreur et pas en fonction de l’amplitude comme pour le régulateur P. C’est pour cette raison qu’il réagit beaucoup plus rapidement qu’un régulateur P. Même face à une petite erreur il va générer une grosse valeur régulée dès lors qu’il y a une variation d’amplitude de l’erreur.
Le régulateur D sera inefficace face à une erreur résiduelle permanente, quel que soit sa valeur puisque celle-ci reste constante (pas de variation d’amplitude donc pas de réaction du régulateur). C’est pourquoi ce type de régulateur sera rarement utilisé seul dans la pratique, il est couramment associé à un régulateur de type P.
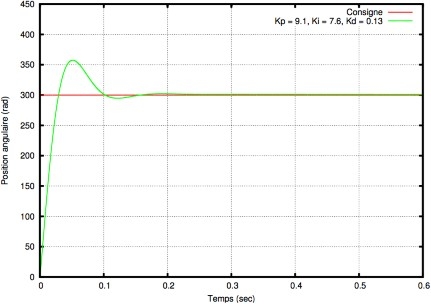
Fig.I.9 Régulateur Dérivé
I.7.5Régulateur PID
Le régulateur universel PID s’obtient donc en ajouter une composante de Type D à un régulateur PI. Comme pour un régulateur PD, la partie dérivée assure une plus grande rapidité pour atteindre la valeur de consigne en ajoutant une action anticipatrice au régulateur.
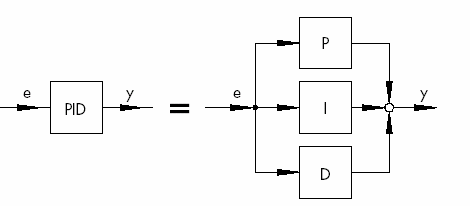
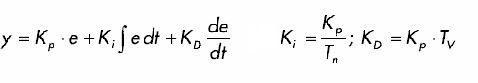
Fig.I.10 Régulateur PID
I.8- Type de régulateurs
I.8.1 Régulateur tout ou rien
La propriété essentielle d’un régulateur tout ou rien réside dans le fait qu’il ne peut prendre que deux états. Il peut de ce fait être considéré comme le régulateur le plus simple.
Ce type de régulateur sera utilisé quand la simplicité de réalisation de la régulation prévaut sur l’observation stricte de la consigne ou encore lorsque la valeur régulée ne peut pas être de type continu. La régulation tout ou rien est illustrée sur le graphe ci-dessous :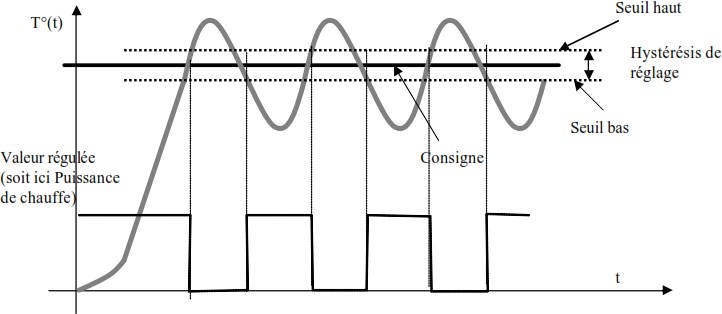
Fig.I.11 Régulateur tout ou rien
I.8.2Régulateurs continus
Les régulateurs discrets précédemment abordés ont pour principal avantage leur simplicité de mise en œuvre et de réalisation qui les rend par conséquent beaucoup moins coûteux que les régulateurs continus.
I.8.3Régulateurs numériques
Jusque-là, seuls les régulateurs analogiques (continus) ont été considérés, c’est-à-dire, ceux qui à partir d’une erreur analogique calcule une valeur régulée, elle aussi de type analogique.
Ci-dessous, le schéma classique d’une telle régulation :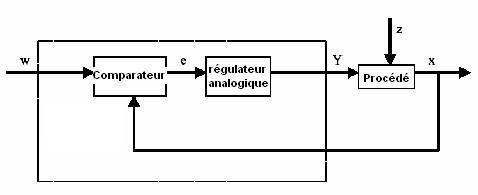
Fig.I.12 Régulateur Analogique
Pourtant, il est bien souvent avantageux de travailler avec une erreur de régulation de type numérique. D’une part parce que l’algorithme reliant l’erreur et la sortie du régulateur va, pouvoir être réalisé en programmant un ordinateur ou calculateur, offrant ainsi une plus grande flexibilité que ne le fait une réalisation par circuit analogique.
D’autre part, l’électronique numérique permet une plus grande possibilité d’intégration des circuits, de telle sorte que plusieurs régulateurs peuvent être contenus dans un très petit espace.
Il est enfin possible d’utiliser le même ordinateur pour gérer plusieurs boucles de régulation si sa capacité le permet.
Pour rendre possible un traitement numérique des données de régulation, il est nécessaire de placer un convertisseur analogique – numérique (CAD) sur la branche de mesure.
L’erreur sera ensuite réalisée grâce à un comparateur numérique en soustrayant la mesure et la consigne pour donner une erreur numérique (entrée du régulateur).
La sortie numérique du régulateur sera ensuite traitée avec un convertisseur numérique – analogique (CDA), afin d’obtenir une sortie du système de type analogique. L’ensemble convertisseur, comparateur et régulateur ont, vu de l’extérieur, les même propriétés qu’une régulation analogique.
La structure d’une régulation numérique est représentée sur le schéma suivant :
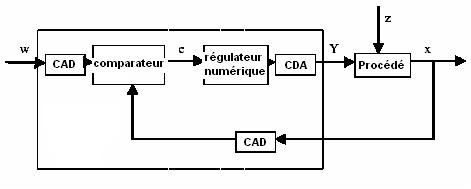
Fig.I.13 Régulateur Numérique
En plus des avantages évidents que comporte le régulateur numérique, il pose en soi tout de même divers problèmes, et notamment celui de la précision de la numérisation. Les critères pour une bonne régulation numérique sont :
- La résolution du Convertisseur numérique analogique.
Elle permet de choisir la finesse avec laquelle sera reconstitué le signal analogique. La résolution doit être choisie de telle sorte qu’aucune information utile à la régulation ne soit perdue.
- La fréquence d’échantillonnage du convertisseur analogique – numérique.
C’est la fréquence avec laquelle le convertisseur analogique – numérique va mesurer le signal analogique et le numériser. Cette fréquence doit être suffisamment élevée pour que le régulateur puisse réagir même à de petits changements de la sortie.
- La fréquence d’horloge.
Un calculateur numérique fonctionne différemment d’un régulateur analogique, il est commandé par une fréquence d’horloge. La vitesse de calcul de l’ordinateur doit être assez élevée pour qu’aucune modification significative de la sortie n’ait lieu pendant un même cycle de calcul.
Un régulateur numérique doit avoir, vu de l’extérieur, une qualité comparable à un régulateur continu, tant en précision qu’en rapidité de réaction, pour pouvoir être utilisé.