Modèle de SOLOW, Théorie de la Croissance économique

Le modèle de SOLOW, Théorie de la Croissance économique

Relation Capital Humain – croissance économique – Chapitre I.

Ce chapitre aborde de façon théorique la relation existant entre le capital humain et la croissance économique. Il est subdivisé en deux sections.
La première section présente les théories de la croissance économique en partant du modèle de SOLOW(1956) qui est le point de départ de plusieurs tentatives visant à expliquer analytiquement les différentiels de revenus entre les pays.
La deuxième section par contre discute sur le rôle du capital humain dans le processus de la croissance économique à long terme.

I.1. Théories de la croissance économique

La croissance économique, par son importance en termes de création de richesses, de prospérité et d’amélioration des niveaux de vie a été et continue d’être l’une des préoccupations majeures de la science économique.
PERROUX(1958) la définit comme « l’augmentation soutenue pendant une ou plusieurs périodes longues, d’un indicateur de dimension, le produit global net en termes réel ».
Les principales questions abordées par cette riche littérature sont liées à la vitesse de croissance :
Qu’est ce qui explique que certaines nations connaissent des taux de croissance plus rapide que d’autres, autrement quels sont les déterminants de la croissance économique.
Plusieurs modèles de croissance ont été proposés dans ce sens. La théorie moderne de la croissance économique trouve ses origines dans les contributions de SOLOW et SWAN dans les années 50.
Les premiers modèles de croissance néoclassiques considéraient deux facteurs de production, le capital et le travail et mettaient l’accent sur l’accumulation du capital comme facteur de croissance.
Le modèle de SOLOW proposé en 1956 constitue le point de départ et la pierre angulaire de beaucoup d’analyses et de modèles proposés par la suite. Avant de passer à l’analyse rigoureuse de ce modèle, nous présentons d’abord la comptabilité de la croissance.

I.1.1. Comptabilité de la croissance

La comptabilité de la croissance est une technique qui consiste à décomposer la croissance de l’output selon les contributions de chaque facteur de production, à savoir le capital, le travail et d’attribuer la partie non expliquée par ces deux facteurs au progrès technologique ou à ce qui est communément appelé la productivité totale des facteurs (PGF).
Cette productivité des facteurs est supposée capter l’impact des aspects non tangibles du progrès qui permet au travail et au capital d’accroître leurs productivités. Elle a comme soubassement théorique le modèle de SOLOW.
La comptabilité de la croissance n’est pas une théorie en elle-même et ne permet pas de dire quels sont les facteurs ou instruments de politique économique ou sociale ayant eu les plus d’influence sur la croissance et n’a par conséquent pas d’implications directes en matière de politique économique.
Généralement cet exercice peut être vu comme une étape préliminaire pour l’analyse des déterminants fondamentaux de la croissance économique. Elle suppose évidemment que les facteurs de production sont indépendants des facteurs derrière le changement technologique. La mécanique de cet exercice a pour point de départ une fonction de production néoclassique donnée comme suit :
= (,, ) [1.1]
Où est le niveau de production, est le stock de capital, est la quantité de travail et désigne le niveau du progrès technologique. La décomposition de la croissance de la production dépend évidemment de la spécification de cette fonction.
En différenciant cette équation et en divisant par, on obtient :
Où Y, et Sont les produits marginaux par rapport aux facteurs. L’équation [1.4] représente donc une décomposition du taux de croissance ( ) selon la contribution du facteur capital ( ), la contribution du facteur travail ( ) et une composante due au progrès technique ( ). L’équation [1.4] permet également de dénicher les sources de la croissance économique.
Ainsi, la première source de la croissance économique c’est l’investissement; la seconde est la main d’œuvre (le travail) et enfin, la troisième source est le progrès technique. Ce dernier améliore les procédés de production en augmentant la productivité marginale de facteurs que l’économie utilise.

I.1.2. Le Modèle de SOLOW

Afin de comprendre l’apport de la croissance endogène, il n’est pas inutile de repartir du modèle traditionnel néoclassique de croissance exogène tel que celui proposé par SOLOW(1956). SOLOW expose son modèle de croissance dans un article publié en 1956 (qui lui vaudra le prix Nobel en 1987).
Non satisfait des résultats du modèle HARROD-DOMAR qui prévoyait une croissance économique instable, son objectif est de présenter un modèle où il est possible d’obtenir une croissance stable et pérenne à long terme.
n respectant les hypothèses standards du modèle néoclassique – une situation de concurrence parfaite où toutes les entreprises sont « Price-takers », la substituabilité des facteurs de production, la constance des rendements d’échelle et les convexités des techniques de production – le modèle de SOLOW souhaite poser les bases d’une théorie capable de conduire à un taux de croissance d’équilibre qui assure le plein emploi mais qui coïncide également avec l’optimum social.
Ce qu’il va réussir en partie. Néanmoins, ce modèle, dans sa version initiale aboutit à une croissance bornée amenant l’auteur à intégrer un changement technique « exogène » pour obtenir un taux de croissance par tête positif à long terme.
En effet, SOLOW a voulu répondre à la question de savoir pourquoi certains pays sont riches et d’autres pauvres. Sur ce, il s’est servi des deux équations fondamentales à savoir : la fonction de production et la fonction d’accumulation du capital pour répondre à cette préoccupation.
La fonction de production renseigne sur le produit qu’une économie peut réaliser à l’aide de sa technologie et des facteurs de production dont elle dispose. La fonction d’accumulation du capital par contre décrit le processus de formation du capital physique.

1.1.2.1. Le Modèle sans progrès technique de base

Le modèle de SOLOW considère une économie qui a un seul bien produit à partir de deux inputs, le capital (K) et le travail (L), selon une fonction de production néoclassique agrégée reliant le niveau de production (Y) aux deux facteurs de production, de la forme :
= (, ) [1.5]
Cette fonction de production vérifie un certain nombre de propriétés qui vont permettre l’existence, l’unicité et la stabilité de l’équilibre de long terme.
• Les dérivées partielles premières sont continues, positives et décroissantes ( > 0, > 0, < 0, < 0), traduisant ainsi les rendements marginaux décroissants pour chacun des inputs, pris séparément. C’est-à-dire que, si l’on maintient constant le niveau de l’un des deux facteurs, le travail par exemple, et que l’on augmente la quantité de l’autre, la production va effectivement augmenter, mais dans des proportions de plus en plus faibles.
• La fonction de production est ensuite homogène de degré un, ce qui implique que les rendements d’échelle sont constants :
F(λK, λL) = λF(K, L) avec >0
Autrement dit, si on double la quantité de chacun des inputs, la production double exactement. Cette hypothèse suppose en particulier que les facteurs de production autres que le capital et le travail, sont relativement insignifiants.
• La fonction de production doit remplir les conditions de régularité fixée par Inada, soit :
( ) lim
, →
(. ) = 0 ( ) lim
, →
(. ) = ∞ (c) F (0, L) =F (K, 0) =0
Les conditions (a) et (b) veulent tout simplement dire que plus un facteur est abondant, moins élevé sera sa productivité marginale et moins abondant est un facteur, plus élevé sera sa productivité marginale. La condition (c) signifie que pour produire, il faut la présence de ces deux facteurs de production. Sans l’un ou l’autre la réalisation de la production est impossible. Cette condition traduit l’essentialité des facteurs de production.
La deuxième équation fondamentale du modèle d’accumulation du capital : de SOLOW est la fonction
= − = − [1.6]
La variation du stock de capital est égale à la différence entre l’investissement et la dépréciation du capital. Le stock de capital se déprécie d’une période à l’autre à un taux constant ( ), au cours du processus de production. Comme l’économie en question est fermée, l’épargne sert exclusivement à l’accumulation du capital domestique. La constance des rendements d’échelle nous permet d’écrire la production et le capital en variables par tête.
Si on pose =, = alors la fonction de production par habitant peut être exprimée sous cette forme :
= = (, ) =, 1 = ( ) [1.7]
Où y est la production par habitant et k le stock de capital par habitant.
Comme le capital par tête s’écrit =, en faisant intervenir les logarithmes et en le dérivant par rapport au temps, il vient :
= − [1.8]
̇Puisque = − = −, alors = − [1.9]
Où est le taux d’accumulation du capital par tête, est le taux d’accumulation du capital
̇et le taux de variation de la population active. On suppose que ce dernier croit à un taux
̇fixe : =
En réaménageant les termes de l’équation [1.9], l’équation de la dynamique du capital peut s’écrire de la sorte :
= ( ) − ( + ) [1.10]
Il ressort de l’équation [1.10] que la dynamique du capital dépend positivement du niveau d’investissement par tête ( ( )) et négativement du niveau de la dépréciation du capital par tête. L’économie atteint son sentier de croissance équilibré(SCE) si et seulement si la condition suivante est vérifiée : ̇ = = 0 ⇔ ( ) = ( + ) .
Cette situation peut être présentée graphiquement comme suit :
 

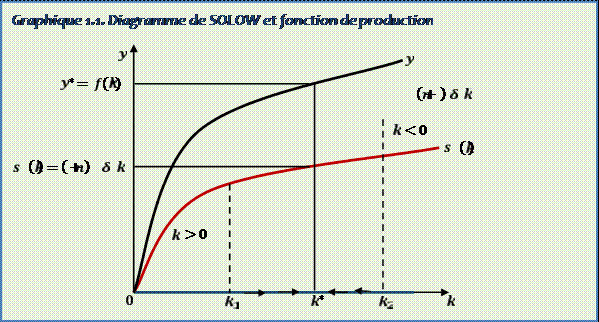
Graphique 1.1. Diagramme de SOLOW et fonction de production 22
Ce graphique montre que si l’économie se situe au niveau de l’intensité capitalistique k1, l’investissement est supérieur aux taux effectif de dépréciation du capital, elle aura tendance à aller vers k* alors que si elle se trouve au point k2, elle aura tendance à rentrer vers k* parce que l’investissement est inférieur au taux effectif de dépréciation. Bref, l’intensité capitalistique aura tendance à croitre pour tout niveau de k<k* et décroitre pour tout niveau de k>k*.
Ainsi, au steady state le taux de croissance de l’économie s’annule; par conséquent, le modèle de croissance néoclassique sans progrès technique ne peut représenter qu’une croissance de moyen terme, lorsqu’une économie dont le stock de capital par tête est inférieur à sa valeur d’équilibre stationnaire converge vers cette valeur d’équilibre.
Une fois parvenue à l’équilibre stationnaire, l’économie cesse de croitre. Il est dès lors possible d’obtenir une croissance de long terme si on spécifie un changement technique exogène qui peut déplacer la fonction de production au cours de temps.
C’est ainsi que la seconde version du modèle prend en compte le progrès technique pour expliquer l’évolution du stock du capital par tête à long terme. Le progrès technique ici porte essentiellement sur le facteur travail et permet d’améliorer sa productivité ou son efficacité; c’est l’hypothèse de la neutralité du progrès technique au sens de HARROD.

1.1.2.2. Le Modèle de SOLOW avec progrès technique

Le modèle de SOLOW sans progrès technique n’arrive pas à expliquer le maintien de l’écart de revenu par tête entre les pays riches et les pays en développement.
C’est pour chercher une réponse à cette contradiction que SOLOW (1956) arrive à la conclusion que la croissance du stock de capital et du travail n’est pas l’unique facteur expliquant la croissance réelle de la production des pays développés mais qu’il existe une autre source de croissance.
Il prend donc en compte un troisième facteur qu’il nomme « facteur résiduel » ou « trend de progrès technique » qui traduit ce que les facteurs capital et travail n’expliquent pas. Il introduit alors le progrès technique comme une tendance à l’augmentation de l’efficacité du travail. Le facteur travail devient ainsi « travail efficace ».
On spécifie alors une nouvelle fonction de production où le facteur « travail efficace » est obtenu comme étant le produit entre le « travail proprement dit (L) et d’un facteur d’efficacité qui croit à un taux constant » [B. AMABLE, 1989]8. Le progrès technique selon SOLOW est exogène et neutre au sens de HARROD, c’est-à-dire, le progrès technique modifie la productivité du facteur travail (L).
Car puisque la démographie détermine la main d’œuvre disponible dans l’économie, le progrès technique augmente l’efficacité d’unité de travail.
La fonction de production néoclassique se réécrit donc :
= (, ) [1.11]
En divisant chaque terme de cette fonction par AL, il vient :
= ( ) Avec = = qui représentent respectivement le produit et le capital par unité d’efficience et cette dernière croit au taux.
En utilisant les mêmes développements comme au modèle simple, on trouve aisément l’équation de l’évolution du capital dans le temps :
= ( ) − ( + + ) [1.12]
L’état stationnaire ou régime permanent est atteint lorsque l’intensité capitalistique devient constante, c’est-à-dire on vérifie que : ( ∗) = ( + + ) ∗
A l’état stationnaire, le taux de croissance du capital par unité d’efficience, est nul tout comme celui de la production par unité d’efficience . Le produit par travailleur
= ( ) croit au taux et le produit global Y croit au taux :
= + [1.13]
Somme toute, le modèle de SOLOW montre que seul le progrès technique peut expliquer les niveaux de vie en hausse persistante, c’est-à-dire le caractère autoentretenue d’une croissance enrichissante [NSHUE, 2007]. Ce modèle vaut encore son pesant d’or puisqu’il est le premier à avoir mis en évidence le rôle du progrès technique dans le processus de croissance économique à long terme.

1.1.2.3. Limites et dépassement du Modèle de SOLOW

Les analyses théoriques des facteurs explicatifs de la croissance économique ont évolué dans le temps. C’est SOLOW (1956) qui a montré qu’il existe une croissance de long terme stable, dont le rythme ne dépend que des évolutions de la population et de la technologie.
Pour lui, la croissance suppose donc un développement du capital par l’investissement et un accroissement de la population.
La croissance est dans ce cas bornée par un rythme d’accroissement naturel considéré comme une donnée exogène. La croissance du capital est quant à elle limitée par la loi des rendements décroissants, et à long terme les rendements d’échelle constant.
Le modèle de SOLOW inclut néanmoins le progrès technique, susceptible d’améliorer la productivité des facteurs. Mais il s’agit d’un progrès technique exogène, c’est-à-dire non expliqué par l’analyse économique. Cette externalisation de facteurs de production réduit ainsi le pouvoir explicatif de ce modèle de croissance.
En effet, un défaut majeur du modèle de SOLOW est que le taux de croissance de long terme dépend de deux facteurs (taux de croissance de la population et niveau du progrès technologique) qui ne sont pas déterminés par le modèle lui-même, ils sont exogènes au modèle.
Pour la croissance de la production par tête, seul le progrès technologique importe, et puisque cette variable est exogène dans le modèle, le taux de croissance de la production par tête lui-même est exogène.
Donc ce n’est pas une théorie de croissance endogène dans laquelle le taux de croissance du PIB par tête est déterminé par le modèle. C’est dans ce contexte que les nouvelles théories de la croissance endogène remettent en question l’idée d’un progrès technique exogène du modèle de SOLOW.
Une seconde limite du modèle parait évidente sous l’hypothèse de la décroissance de la productivité marginale du facteur capital qui stipule que le taux de croissance du stock du capital per capita ainsi que sa productivité marginale diminue avec l’augmentation du stock de capital, et si le progrès technique est le même partout dans le monde, les pays en développement doivent rattraper les pays développés.
Or, il n’en est rien du tout concernant beaucoup de pays en développement.
En réaction aux défauts de la théorie néoclassique de la croissance et de son incapacité à expliquer une partie des faits observés, le milieu des années 80 a vu émerger un groupe de modèles expliquant la croissance à long terme de façon endogène par la relaxation des hypothèses de rendements décroissants du capital et en rendant le progrès technique endogène au modèle.
Ces théories sont qualifiées de théories de croissance endogènes par ce qu’elles cherchent à expliquer la croissance par des variables déterminées de façon endogène dans le modèle.
Les principaux apports de ces théories consistent d’une part dans l’introduction de l’éducation et le remplacement de la vision restreinte du capital comme étant le stock physique par une notion plus large incluant le savoir et le stock de connaissances accumulées dans la nation, on parle alors de capital humain et par conséquent le rôle de l’éducation est mis en exergue.
Il consiste d’autre part, dans l’introduction de la possibilité d’externalités. Ces externalités qui proviennent de la diffusion du savoir et des bénéfices externes du capital humain contribuent à faire obstacle aux rendements décroissants du capital physique accumulé.
Le développement de la recherche et développement et le processus d’innovation, facteur central dans ces modèles dépend ou peut être influencé par les politiques publiques (incitations fiscales, protection des droits de propriété intellectuelle, fourniture d’infrastructure de services, etc.) La conséquence de ceci est que le taux de croissance à long terme peut être influencé par les interventions publiques. L’Etat a donc un rôle important à jouer dans la détermination du taux de croissance économique à long terme.
En somme, les théories de la croissance endogène mettent ainsi en évidence quatre facteurs qui influent sur le taux de croissance d’une économie. Les infrastructures publiques constituent donc un facteur de croissance qui engendre des rendements croissants à long terme en raison des économies internes qu’elles permettent pour les producteurs privés.
Une analyse de BARRO en 1990 a soulignée ainsi que les infrastructures facilitent la circulation des informations, des personnes et des biens. L’impôt destiné à financer ces investissements, joue dans ce cadre un rôle positif sur la croissance et non seulement un effet de désincitation sur le secteur privé.
La recherche développement, introduite dans les travaux de ROMER, est considérée comme une activité à rendement croissant, du double fait que la connaissance est un bien non rival et que le coût de son appropriation est pour chaque chercheur minimal.
La croissance économique résulterait ainsi d’une activité d’innovation, engagée par des agents qui espèrent en tirer profit. Ce faisant, le progrès technologique prend une place importante dans la croissance économique, de même que l’éducation et la R & D qui constituent l’une des principales sources d’innovation technologique. Ce type de modèle lie donc la croissance au stock de capital humain existant [nous y reviendrons au point 1.2.2].
LUCAS (1988), quant à lui, élargit le concept de capital et suggère que l’accumulation du capital humain serait le moteur même de la croissance à cause des effets externes qui affectent les rendements décroissants dans la production. Ce capital est défini comme le stock des connaissances valorisables économiquement et incorporés aux individus (qualification, état de santé, hygiène,…).
LUCAS développe dans son analyse, le capital humain qui est volontaire, qui correspond à une accumulation de connaissances (Scholling) et l’accumulation involontaire (Learning by doing).
En outre, la productivité privée du capital humain a un effet externe positif car, en améliorant son niveau d’éducation et de formation, chaque individu augmente le stock du capital humain de la nation et par la même contribue à améliorer la productivité de l’économie nationale.
Dans la lignée des travaux de ROMER (1986), d’autres recherches attribuent la croissance économique à l’accumulation de capital physique. Ils ne rompent pas totalement avec l’hypothèse des rendements constants, car ils considèrent qu’il en va ainsi pour chaque entreprise; mais qu’en revanche, il existe des rendements d’échelle croissants liés aux externalités positives des investissements. Ainsi, le Learning Spillover, du fait de la circulation de l’information, permet aux entreprises de bénéficier de l’accumulation des savoirs faire entrainer par l’accumulation du capital physique.
_______________________________
8 Cité par GOMBOR.A, 2011