La forme faible de l’efficience des marchés financiers
III- Les trois formes de l’efficience
Dans le but de réaliser des tests statistiques plus fins, Fama a défini trois formes de l’efficience des marchés financiers.
- La forme faible ou hypothèse faible de la théorie de l’efficience prétend qu’il n’est pas possible de tirer parti des information passés concernant un actif financier pour prévoir les révoltions futurs du prix de cet actif.
- La forme semi forte ou l’hypothèse semi forte de la théorie de l’efficience prétend qu’il n’est pas possible de tirer parti des information concernant un actif financier au moment même où ces informations sont rendues publiques pour prévoir les révoltions futurs du prix de cet actif.
- La forme forte ou l’hypothèse forte de la théorie de l’efficience prétend qu’il n’est pas possible de tirer parti des information non publiques concernant un actif financier au moment même où ces informations sont rendues publiques pour prévoir les révoltions futurs du prix de cet actif.
a) La forme faible de l’efficience et les tests de prévision des cours
1- Définition et implications de la forme faible de l’efficience
La forme faible consiste à énoncer que le prix actuel d’un actif financier est totalement indépendant de l’ensemble des informations concernant ce titre publié dans le passé.
On ne peut donc utiliser l’ensemble des informations passées pour déminer de façon certaine le prix actuel ou l’évolution de prix.
Deux remarques paraissent importantes à formuler à ce point du raisonnement.
- Les investisseurs ont déjà analyse l’ensemble des informations diffusées dans les passées et les ont déjà répercutées dans les cours.
- Rien n’empêche les analystes financiers d’utiliser les informations passées concernant un actif financier ou une entreprise pour tenter de prévoir l’évolution du prix d’un actif.
En autres termes, l’hypothèse de l’efficience peut se résumé aux affirmation suivantes : les prix à l’instante t de chaque actif financier est totalement indépendant du prix du même actif à la période t-1 ou aux autres périodes précédents.
E(Pj,t+1 / Φj) = Pj,t
Il en résulte qu’en moyenne, la meilleure prévision d’évolution du prix d’un actif financier à la période t+1 reste son prix connu dans la période t.
Cette impossibilité de prévoir de façon certaine l’évolution du prix d’un titres à partir du cours passées amène la remise en cause de pratiques pourtant très utilisées : l’analyse fondamentale et l’analyse technique.
2- L’analyse fondamentale et l’analyse technique
2.1- L’analyse fondamentale
L’analyse fondamentale concerne à l’origine le marché des actions.
Il consiste à analyser l’ensemble des informations économique, comptable…, des entreprises cotées de manière à déterminer leur valeur.
Cette valeur peut être calculée grâce à plusieurs méthodes.
En premier lieu, elle peut apparaître comme la somme de la valeur des ses actifs et de sa capacité à gérer des bénéfices.
L’évaluation comptable consiste en effet à évaluer séparément les actifs de la firme et sa capacité à réaliser des bénéfices puis à additionner ces deux éléments distincts.
Elle peut être déterminée à partir de la somme actualisée de ses bénéfices futurs.
Il s’agit alors d’une évaluation plus financière qui consiste à tenter de prévoir les dividendes futurs de la firme à estimer la somme de ses dividendes actualiser.
D’autres types d’évaluations, prenant en compte des aspects stratégiques ou des anticipations d’évolution du bénéfice.
Les évaluations peuvent varier quelque peu d’un analyste à l’autre.
En théorie, les différents prix successifs des actions de la firme devraient varier autour de la valeur intrinsèque de la firme, ainsi déterminée comme si une force de rappel invisible ramenait toujours les cotations vers la valeur fondamentale.
Cette dernière apparaît alors comme une moyenne sur longue période des prix des actions.
La valeur fondamentale varie cependant en fonction des informations successives concernant l’entreprise ou marché.
Les cotations quotidiennes conserve le prix autour des cette valeur intrinsèque.
Le règle d’arbitrage possible des investisseurs est alors la suivantes : acheter lorsque le cours est située en dessous la valeur fondamentale, vendre lorsque le cours est située en dessus de cette valeur fondamentale.
Le graphique 1 montre les cours varier autour la valeur fondamentale.
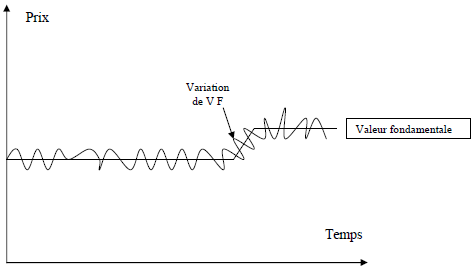
Graphique 1 variation du cours autour de la valeur fondamentale
Le problème est de savoir si l’analyse fondamentale est contraire ou non à la théorie de l’efficience.
Or, il apparaît que l’analyse fondamentale n’est pas opposée à la forme faible de l’efficience.
Il est toujours possible de tenter de déterminer une estimation comptable ou économique de la valeur d’un société ou d’un autre actif financier.
2.2- L’analyse technique
EN revanche, une contradiction existe entre la forme faible et l’analyse technique.
Le principe de l’analyse technique constitue la négation de la forme faible de la théorie de l’efficience.
L’analyse technique se fonde sur l’analyse des séries du cours passés pour tenter de déterminer une tendance d’évolution des prix des titres ou pour permettre prévoir les hausses ou baisses des cours.
L’analyse technique se fonde sur des graphiques opposant le prix du titre en ordonnée et le temps en abscisse.
Les principaux principes de l’analyse technique sont :
Les lignes de résistance et les supports :
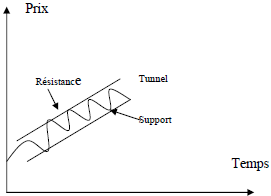
Graphique 2 supports et résistance
Il s’agit de seuils qui empêchent la progression du marché.
Ainsi les cours butent sur les lignes de résistance et sur les supports sans parvenir à les franchir.
Lorsque les cours varient pendant une certaine durée entre une ligne de résistance et support, la combinaison de la ligne de résistance et du support est appelée tunnel.
Lorsque les cours coupe une ligne de résistance, il s’agit d’un signal de hausse : l’investisseur peut acheter le titre qui devrait s’apprécier.
Au contraire lorsque le prix franchit un support, il s’agit d’un signal de baisse.
Les moyennes mobiles :
La méthode des moyennes mobiles constitue à la fois l’une des plus anciennes et l’une des plus utilisées dans le domaine de l’analyse technique.
La moyenne mobile permet de lisser les cours en calculant quotidiennement une valeur égale à la somme des X cours précédents devisée par X, soit : MMx = (Pt +Pt-1 +Pt-2 …+Pt-x+1) / X.
Il est possible d’affiner la méthode en utilisant des moyennes mobiles pondérées ou exponentielles.
Lorsque les courts traversent à la hausse une moyenne mobile, cela constitue un signal d’achat.
Il en est de même lorsqu’une moyenne mobile « courte » c’est-à-dire calculée à partir d’un petit nombre de cours, traverse à la hausse une moyenne mobile « longue ».
Inversement, la traversée à la baisse de la moyenne mobile par le cours ou d’une moyenne mobile « longue » par une moyenne mobile « courte » constitue un signal de vente.
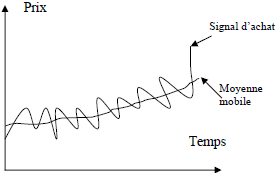
Graphique 3 Les moyennes mobiles
Le momentum : Le momentum est censé représenter la vitesse d’évolution des cours. Lorsque est dans une phase d’accélération haussière et baissière, le momentum augmente.
Le momentum s’obtient en calculant jour après jour la différence des cours pour un intervalle de temps donné.
La formule d’un momentum à x jours est :
M(X jours) = Ct – Ct-x où Ct est le cour du jour t
Le RSI (relative strength index) : le RSI appartient à la famille des oscillateurs. Il est donc censé mesurer l’évolution de la vitesse de croissance ou de baisse d’un titre.
Il doit permettre de prévoir de façon fine les changements de tendance. Il se calcule de la façon suivante :
RSI (X jours) = 100 – [100 / (1+RS)
RS = Moyenne de hausse / Moyenne de baisse
Le RSI est borné et varie entre 0 et 100. Lorsque le marché est en forte hausse ; le RSI tend vers 100, il tend vers 0 lorsqu’il est en baisse.
Lorsque le RSI passe d’une valeur supérieure à 70 à une valeur inférieure, cela est censé constituer un signal de vente.
Un signal d’achat est constitué par un passage d’une valeur inférieure à 30 à une valeur supérieure à 30.
Les oscillateurs stochastiques : le concept de base est de dépister la naissance d’une nouvelle tendance en mesurant la différence entre le prix de clôture, le plus haut et le plus bas d’une série de cours.
Pratiquement, une stochastique d’ordre D est calculée de la manière suivante.
%D (x jours) = 100 * [(C-Lx) / (Hx – Lx) C la dernière cours de clôture
Lx le cours le plus bas
Hx le cours le plus haut
Les méthodes d’analyse technique ne sont fondées sur aucune analyse théorique ou étude empirique.
Elles proviennent simplement d’observation non systématiques et des règles initiées sans réel fondement scientifique.
3- Les tests d’efficacité des méthodes systématiques de spéculation
Si les méthodes graphiques apparaissent comme des méthodes systématiques de spéculation, elles ne sont pas les seules méthodes existantes.
Ainsi le méthode des filtres est une méthode ancienne dont les conséquence ont été soulignées lors du Krach 1987.
Cette méthode consiste à acheter systématiquement un actif présélectionné lorsque le prix de l’actif augmente de X% ou plus et de le revendre lorsque le cours baisse de plus de X%.
La valeur de filtre X est déterminée au début des processus dès l’investisseur. Fama et Blume (1966) ont testé l’efficacité de la méthode.
Ils ont comparé la rentabilité d’un portefeuille géré par la méthode de filtre avec une méthode de gestion passive.
Le méthode de gestion passive consiste à acheter l’ensemble du portefeuille à un instant donné et à le revendre entièrement à la fin de période du test.
Ils ont également géré un portefeuille en fonction des signaux d’achat et de vente donnés par la méthode des filtres. Ils ont utilisé tous les filtres possibles allant de 0.5% à 20%.
Ils ont comparé les résultats des portefeuilles gérés selon les deux méthodes.
Seul le filtre de 0.5% donne une rentabilité supérieure à celle du portefeuille en absence des coûts des transactions.
Dumontier (1989) a testé la profitabilité des moyennes mobiles sur les marchés des actions de paris.
Il a utilisé la même méthode que celle de Fama et Blume.
Il a comparé la rentabilité d’un portefeuille géré de façon passive avec de portefeuille gérés de manière active grâce au moyennes mobiles.
Il a utilisé deux types des portefeuilles gérés avec la méthode des filtres : les premiers tiennent compte d’un délai de confirmation, les secondes ne tenant pas compte d’un délai confirmation.
Le coût de transaction est 1%.
La stratégie fondée sur l’utilisation des moyennes mobiles donne des résultats inférieurs à la stratégie passive.
Il conclut que l’utilisation de la méthode des moyennes mobiles ne nous parait pas fondée, aussi de point de vue théorique que le point de vue empirique.
4- Les tests d’auto covariance et d’auto corrélation
Les tests de covariance et auto corrélation sont des tests statistiques les plus simples permettent de mettre en évidence une éventuelle dépendance entre le rendement d’un actif à la période p et le rendement du même actif lors des périodes antérieures.
Ces tests sont réalisés avec une seule série de rendement d’un seul actif dont les périodes sont décalés dans le temps.
Il est possible de créer plusieurs séries chronologiques à partir d’une seule et ainsi de calculer des corrélations entre ces nouvelle séries.
Les tests les plus simples consistent ensuite à calculer les covariances et le cœfficient de corrélation entre la première série et séries suivantes.
On appelle auto corrélation d’ordre n le cœfficient de corrélation observé entre le série S0 et SN.
Le cœfficient d’auto corrélation ρn = COV (R0, Rn) / σ(R0) . σ(Rn)
Si le série n’est pas auto corrélée, l’hypothèse H / ρ = 0 est vérifiée.
5- Les tests des changements de signe (runs)
Une autre forme de test simple permettant de se prononcer sur le caractère aléatoire des séries de prix (rendement) concerne les changements de signes.
Dans une série chronologique de nombres aléatoires, le nombre de changements de signes – série de rendements positifs suivie d’une série de rendements négatifs – devrait suivre une loi normale.
Fama (1965) a testé cette hypothèse.
Il a observé un nombre des changements de signe inférieur à la moyenne, ce qui révèle une corrélation positive.
Toutefois, les corrélations positives sont trop faibles pour qu’in investisseur puisse, compte tenu des niveaux des coût de transaction, en tirer parti.
6- Les test plus élaborés de marché aléatoire et de quasi-marché aléatoire
Il existe de nombreux tests permettant de comparer une série statistique à une série de nombres aléatoires de manière à observer si la série testée suite ou non à un marché aléatoire.
Le premier test est celui de BOX et Pierce (1970).
La méthode de BOX et Pierce consiste à tester l’auto corrélation des résidus (ε) de l’équation de marché aléatoire.
En effet, si les résidus d’une telle équation sont auto corrélée, on pourra dire que la série n’est pas marchée aléatoire.
On peut calculer statistique de BOX et Pierce telle que.
Q1(q) = q . Σp^2(k)
Qui suit une loi du X2 à q-1 degrés de liberté.
La série est réputée suivre une marché aléatoire pour un seuil de confiance défini si Q1(q) est inférieure à la valeur du X2 à q-1 degrés de liberté.
Q est le nombre d’observation et p^(k) est le cœfficient d’auto corrélation d’ordre k des résidus.
6.1- Le test de racine unitaire
Le test de racine unitaire, par exemple celui de Dickey-Fuller, consiste à tester l’hypothèse ![]() , contre l’hypothèse alternative
, contre l’hypothèse alternative ![]() , dans l’équation suivante:
, dans l’équation suivante:
Le deuxième terme à droite de l’équation a pour but de corriger le problème d’autocorrélation.
Dans le cas d’indépendance sérielle , et par conséquent le test de racine unitaire Dickey-Fuller augmenté est identique au test Dickey-Fuller.
Les valeurs critiques sont identiques à celles du test antérieur.
6.2- Les tests de quasi-marché aléatoire
Alexandre (1992) propose un test à fait nouveau afin de vérifier la réalité de la forme faible de l’efficience des marchés financiers.
Il va tester l’hypothèse d’efficience des marchés en utilisant u processus statistique dans lequel les rendements sont indépendants les uns des autres mais dont la variance des rendements est dépendante de la variance des rendements précédents.
Alexandre propose de tenir en compte de l’évolution de la variance en utilisant les processus ARCH.
Xt+1 = αXt + εt
Où εt suit un processus ARCH d’ordre p, c’est-à-dire si :
εt = utht avec ut = N(0,1)
h2t = α0 + Σ αi ε2 t-1
Avec l’espérance nulle et le variance égale h2t
Si l’espérance de εt demeure nulle, sa variance intègre le passé et devient ainsi un processus à mémoire.
Alexandre soumet les résultats obtenus à l’aide de la modélisation de ses données par une quasi-marche aléatoire au test d’auto corrélation, de BOX et Pierce, ….
Ses conclusions sont les suivantes « la quasi-marche aléatoire accepte l’hypothèse d’efficience liée dans 87,7% des cas.
Dur de la donnée mensuelle, plus qu’ailleurs le débat reste ouvert.
Or, on constat ici qu’en intégrant la volatilité des cours dans le modèle on aboutit à des conclusions en faveur de l’efficience de manière plus marquée.
Le rejet de l’hypothèse pourrait être plus souvent due certaines fois à une mauvaise spécification des l’hypothèse sous jacentes qu’a de réelles imperfections de marché ».
A cote de ces tests, il existe un test plus complexes, mais peut être moins faible est : les test d’analyse spectrale la co-intégration et le bootstrap.
7- L’analyse spectrale la co-intégration et le bootstrap
7.1- L’analyse spectrale et co-spectrale
Un certain nombre d’investisseur a cherché à prévoir les variations des cours boursiers en observant si, avec un décalage temporel, ces variations n’étaient pas fonction d’autres données.
Par ex, ces investisseurs cherchent e mettre en évidence une possible relation entre les cours de bourse de NY et le bourse de paris.
Si une telle relation existait, elle permettrait à des investisseurs de prévoir à l’avance l’évolution des cours à paris.
L’existence de telle relation remet en cause le principe de la forme faible de l’efficience des marchés financiers puisque l’analyse dans les passés permet de prévoir l’évolution future des cours.
Il convient deux remarques :
- -La mise en évidence de telles relations n’a d’intérêt pour les investisseurs que dans la mesure où elles sont décalées dans le temps.
- L’hypothèse faible de l’efficience n’implique pas que les informations utilisables ne concernant que l’entreprise ou le marché dont on cherche à prévoir l’évolution des cours.
Deux tests principaux, permettant la mise en évidence de telles relations, ont été utilisé.
L’analyse spectrale est une méthode d’analyse développée à l’origine par Granger et Morgenstern (1970).
Elle consiste à décomposer une série stationnaire en cycles de type sinusoïde afin détecter si cette série peut être analysée comme une succession de cycles identiques.
Dans ce cas, la détection du début d’un cycle permet de prévoir l’évolution future de la série.
On peut écrire : Xt – η = Σ ei.w.t .dz(w)
Avec Xt la série, η la moyenne de la série, w=2. Π. F, la fréquence angulaire et dz(w) un processus indépendant, f la fréquence (n de cycles par unité de temps), T= 1/f, mesure de la période.
L’analyse co-spectrale consiste à juxtaposer l’analyse spectrale de plusieurs séries chronologique de même taille afin de mettre en évidence les relations stables entre les variables Xt de la première série et les variables de la seconde série.
L’utilisation d’un décalage de n période permet de mettre en évidence une dépendance autorisant la prévision de X à partir de Y.
L’utilisation de l’analyse spectrale a amené des conclusions contractées.
Si la première étude de Granger conclut à l’inexistence de relations entre les indices boursiers étudiés.
Des études plus récentes ont permis de mettre en évidence l’existence de relation entre les indices des différents pays.
7.2- La co-intégration
Paget- Blanc (1994) propose la définition suivante de la co-intégration : » soit deux variables x et y intégrées d’ordre 1, c’est-à-dire stationnaires après différenciation du premier ordre :
x et y sont dite co-intégrées s’il existe une combinaison linéaire unique de la forme xt = A + B. yt +zt où A et B sont des réel quelconques et z est une variable stationnaire de moyenne nulle.
Si l’équation traduit une relation d’équilibre économique alors la variable z permet de mesurer la distance entre le variable x et sa valeur d’équilibre en instant t ».
Si z n’est pas bruit blanc, cela signifie que les deux variables testées sont reliées par une relation économique stable.
Lorsque la co-intégration ainsi testée est vérifié, il est possible d’anticiper avec un certain degré de certitude l’évolution de la série x si l’on connaît les variations y.
7.3- L’utilisation du bootstrap
Acar, Bertin et Lequeux (1994) ont proposé d’utiliser la méthode du bootstrap pour tester l’efficacité des moyennes mobiles sur le marché des changes sur les données quotidiennes.
Les auteurs forment de novelles séries en permettant de manière aléatoire les rentabilités de la série initiale.
La méthode de bootstrap a l’avantage de ne pas nécessiter d’hypothèse concernant la forme de la distribution des rentabilités initiales.
Les critiques liées à la nécessité d’utiliser des séries parfaitement normales avant d’effectuer des tests statistiques complexes n’ont donc plus lieu d’être.
L’ensemble des tests utilisant ces méthodes tend à rejeter l’hypothèse faible de la théorie de l’efficience des marchés financiers.
8- Les possibilités d détermination des rendements des actifs à partir d’un certain nombre des variables : inflation, dividendes et PER.
Certaines études anglo-saxonnes mettent en évidence une série de relations existant entre les rendements d’un titre et certaines données macroéconomique.
Bodie et Nelson (1976) montrent que les rendements des portefeuilles des titres cotes au NYSE varient de manière inverse à l’inflation anticipé.
Fama et Schwert (1977) établissent de leurs cotes une relation négative entre les rendements des portefeuilles et les taux d’intérêt à court terme.
La relation d’arbitrage consistant d’une part à reporter leurs investissements en actions sur les obligations lorsque les taux d’intérêt montent et d’autre part à diminuer la part de leur portefeuille investie en obligations pour reporter ces investissements sur leurs actions lorsque les taux d’intérêt diminuent est connue.
Lorsque les taux diminuent, le prix unitaire du risque en action augment.
Les taux sont moins attractifs, le risque est mieux rémunéré, ce qui encourage l’investissement en actions.
Rozeff et Schiller (1984) mettent en évidence l’existence d’une relation entre la rentabilité des actions et le taux de rendement.
9- Comparaison de quelques études concernant la forme faible de la théorie de l’efficience des marchés financiers
| Articles | Test | Méthodologie | Conclusion |
| Fama et Blume (1966) | Méthode des filtres | Comparaison avec un portefeuille naïf | Validation totale de l’efficience |
| Gaslesne (1975) | Méthode des filtres | Comparaison avec un portefeuille naïf | Validation totale de l’efficience |
| Hamon (1975) | Méthode des points et coix | Comparaison avec un portefeuille naïf | Validation totale de l’efficience |
| Dumontier (1989) | Méthode des filtres | Comparaison avec un portefeuille naïf | Validation totale de l’efficience |
| Gillet et sabatier (1996) | Méthode graphique | Comparaison avec un portefeuille naïf et observation de la rentabilité après signaux | Validation totale de l’efficience |
| Fama (1965) | Auto corrélation | Test d’auto correlation et test d’auto covariance et test de run | Validation totale de l’efficience |
| Solnik (1973) | Auto corrélation | Test d’auto correlation et test d’auto covariance | Validation totale de l’efficience |
| Lo et Mackinly (1988) | Auto corrélation (portefeuille) | Test d’auto correlation et test d’auto covariance et test de run | Validation totale de l’efficience |
| Conrad et haul (1988) | Auto corrélation (portefeuille) | Test d’auto correlation et test d’auto covariance et test de run | Validation totale de l’efficience |
| Fama et french (1988) | Auto corrélation (long période) | Test d’auto correlation et test d’auto covariance et test de run | Validation totale de l’efficience |
| Fontaine (1990) | Auto corrélation | BOX Pierce Co-intégration | Validation totale de l’efficience |
| Alexandre (1992) | Marché aléatoire | Quasi-marché aléatoire | Validation totale de l’efficience |
| Granger et morgenstern (1970) | Analyse spectrale | Analyse spectrale | Validation totale de l’efficience |
| Bertoneche (1979) | Relation inter marché | Analyse co-spectrale | Invalidation de l’efficience |
| Hihhard (1979) | Relation inter marché | Analyse co-spectrale | Invalidation de l’efficience |
| Hakkio et rush (1989) | Relation inter marché | Co intégration | Invalidation de l’efficience |


