Dimensionnement du groupe de propulsion
Cette section traite de l’évaluation des performances et des caractéristiques du groupe de propulsion requis au regard des contraintes de la mission à satisfaire. Spécifiquement, il s’agira tout d’abord de déterminer la poussée maximale que devront développer les moteurs, pour assurer la propulsion de l’aéronef. Par la suite, la poussée unitaire ainsi que les dimensions du moteur seront déterminées.
Poussée maximale des moteurs
La poussée maximale que devrait délivrer les moteurs pour propulser l’avion sera considérer dans ce travail comme étant la poussée disponible desdits moteurs au niveau de la mer. Pour la déterminer, la démarche ici consiste à estimer tout d’abord la poussée requise et la poussée disponible en croisière et, par la suite déduire la poussée maximale au niveau de la mer.
Poussée requise en croisière
En vol subsonique de croisière et sans trainée d’onde, la poussée requise est la poussée minimale nécessaire à l’aéronef pour vaincre la trainée ; ce qui se traduit par l’équation ci- après :
T D 1 V 2SC
R2D
(2.37)
La trainée d’onde étant négligeable (l’avion vole en dessous de Mach 0,8), le coefficient de trainée CD s’exprime comme suit :
37
2
C C kC2 C
k 2W
(2.38)
DD0,bwbLD0,bwb
V 2S
Où CD 0,bwb
est le coefficient global de trainée du BWB au complet (moteurs et empennage
inclus).
La combinaison des équations (2.37) et (2.38) permet d’obtenir l’expression de la poussée requise en croisière, en fonction l’altitude de vol (à travers la densité) et de la vitesse de l’avion.
12kS W 2
TR H ,V
V 2SC
2
D0,bwb
V 2 S
(2.39)
Poussée disponible en croisière
Par définition, la poussée disponible à l’altitude de croisière est la poussée maximale que doivent délivrer les moteurs lorsque l’avion vole à vitesse maximum (Anderson, 1999). En d’autres termes, la poussée disponible en croisière correspond à la poussée requise à vitesse maximale. Analytiquement, cela se traduit par :
Tdispo TR Hcr ,Vmax
(2.40)
12kS
W 2
V
Tdispo
2 Hcr
2
max
SCD0,bwb
V 2 S
(2.41)
Hcr
max
Vmax
est la vitesse maximale atteignable par l’avion en croisière.
Par analogie avec les avions régionaux TAW de taille comparable (cf. annexe 1) tels que le BAe 146, le CRJ 1000 ou encore le ARJ21-900, la vitesse maximale de l’avion pourrait être définie entre 5% et 5,5% supérieure à la vitesse de croisière. Ainsi, pour le BWB la vitesse maximale en croisière sera définie comme suit :
Vmax 1, 0525Vcr
(2.42)
La poussée disponible délivrée par les moteurs à cette altitude devrait être supérieure à la poussée requise pour vaincre la traînée.
38
Poussée maximale au niveau de la mer
Le modèle de poussée de Mattingly (1987) présenté ci-après est un des plus répandu et il a servi de référence à de nombreux travaux sur les moteurs (Roux, 2005 ; Ghazi, et al. 2015). Il permet de déterminer pour un moteur de type turbosoufflante à haut taux de dilution, la poussée générée en fonction de l’altitude et du nombre de Mach de vol. Torenbeek caractérise les turbosoufflantes à haut taux de dilution comme ayant un taux de dilution compris entre 4 et 10 (Torenbeek, 2013). Par ailleurs dans ses travaux, Bardela a montré que le modèle de Mattingly est fiable à plus de 98%, pour la prédiction de la poussée du Cessna Citation X (Bardela, 2017).
T H , M T 0,6 0, 568 0, 251, 2 M 3
(2.43)
dispoSL
Où :
Tdispo
est la disponible pour une altitude et un nombre de Mach donné.
TSL
est la poussée des moteurs au niveau de la mer.
H
SL
est le rapport entre la masse volumique de l’air à l’altitude H et la masse
volumique de l’air au niveau de la mer.
M 0, 9 est le nombre de Mach de vol.
Du modèle de poussée de Mattingly (E-2.43), la poussée totale maximale au niveau de la mer se déduit aisément.
TSL
Tdispo H , M
0,6 0, 568 0, 251, 2 M 3
(2.44)
Poids et dimensions des moteurs
L’estimation de la poussée maximale au niveau de la mer permet par la suite de déterminer le poids et les dimensions du moteur. Raymer (2006) propose les relations suivantes pour se faire.
W 0, 084 T 1,1 e0,045 BPR
(2.45)
engeng
39
L 2, 22 T 0,4 M 0,2
(2.46)
engengmax
D 0, 393T 0,5 e0,04BPR(2.47)
engeng
Où :
Weng Leng Deng
[lb] est le poids d’un moteur en livre.
[in] est la longueur d’un moteur en pouce. [in] est le diamètre d’un moteur en pouce.
Teng
[lb] est la poussée d’un moteur au décollage.
M max Mcr
0, 9
est le nombre de Mach maximal.
BPR est le taux de dilution.
Altitude de vol au maximum de distance
2W
S
k
CD0,bwb
Lorsque l’avion vole à finesse maximale, la poussée est minimale. Cette vitesse qui minimise la poussée est donnée par la relation suivante (Raymer, 2006) :
Vmin
thrust
V L
D max
(2.48)
2W
S
3k
CD0,bwb
Par ailleurs, la vitesse qui maximise la distance parcourue pour un avion à réaction est donnée par la relation suivante (Raymer, 2006) :
Vmax
range
(2.49)
Sachant que la densité de l’air varie avec l’altitude, il est possible de construire la courbe d’évolution de la vitesse de croisière au maximum de distance, en fonction de l’altitude de vol. Les équations (2.50) et (2.51) donnent respectivement l’expression de la densité de l’air dans la troposphère (entre 0 et 11 km) et la stratosphère (entre 11 et 20 km).
40
g0 1
1 H Rair
troposSL
T0
(2.50)
stratos trop
exp gH H
trop
(2.51)
R T
Où :
air trop
SL 1,225
[kg/m3] est la densité de l’air au niveau de la mer.
6, 5103 [K/m] est le taux de variation de la température en fonction de l’altitude
H [m] est l’altitude de vol.
T0 288,15
[K] est la température de l’air au niveau de la mer.
g0 9,81 [m/s2] est la constante gravitationnelle sur terre.
Rair 287
[J/kg/K] est la constante des gaz parfaits.
trop
0,3636 [kg/m3] est la densité de l’air à la tropopause. Ttrop 216,65 [K] est la température de l’air à la tropopause. Htrop 11000 [m] est l’altitude à la tropopause.
Design de la surface verticale et du train d’atterrissage
Cette rubrique présente la méthodologie utilisée pour le dimensionnement de la surface verticale du BWB, ainsi que de son train d’atterrissage.
Design de l’empennage vertical
Les avions de type BWB ne possèdent pas d’empennage conventionnel tel que pour les avions classiques de configuration TAW. En effet, les BWB n’ont pas besoin d’empennage horizontal; par conséquent, leur empennage se réduit aux surfaces verticales. L’empennage vertical est la composante permettant de contrôler les mouvements latéraux de l’aéronef.
41
Procédure de design de l’empennage vertical
Les paramètres qui doivent être déterminés au cours du processus de design de la surface verticale sont les suivants (Sadraey, 2012) :
Surface de l’empennage (Sv) ;
Longueur de bras de levier (lv) ;
Type de profil de la section ;
Allongement (ARv) ;
Effilement (λv) ;
Corde à l’extrémité (Ctv) ;
Corde à la racine (Crv) ;
Corde moyenne aérodynamique (MAC) ;
Envergure (bv) ;
Angle de flèche LE ,V .
Par ailleurs, l’étude de Larkin (2017) sur la stabilité des BWB recommande une inclinaison de la surface verticale d’un angle par rapport à la direction verticale, afin d’améliorer la stabilité de l’appareil.
La figure ci-dessous illustre la procédure de design suivie pour le dimensionnement de l’empennage vertical.
42
Identifier et prioriser les requis du design
Sélectionner le coefficient d’empennage (Cv)
Choisir la position de l’empennage et
déterminer la longueur du bras de levier (lv)
Déterminer l’air totale de l’empennage
Choisir la configuration de l’empennage
Choisir le type de profil de la section
Déterminer l’allongement, l’effilement et l’angle de flèche
Déterminer l’angle de dièdre si
nécessaire
Déterminer l’envergure, la corde à la racine, à
l’extrémité et moyenne
non
Requis de design satisfaits ?
Vérifier la stabilité (statique et dynamique) de l’avion
oui
Fin du design
Figure 2.3 : Procédure de design la surface verticale (adapté de Sadraey, 2012)
43
Détermination des paramètres de l’empennage vertical
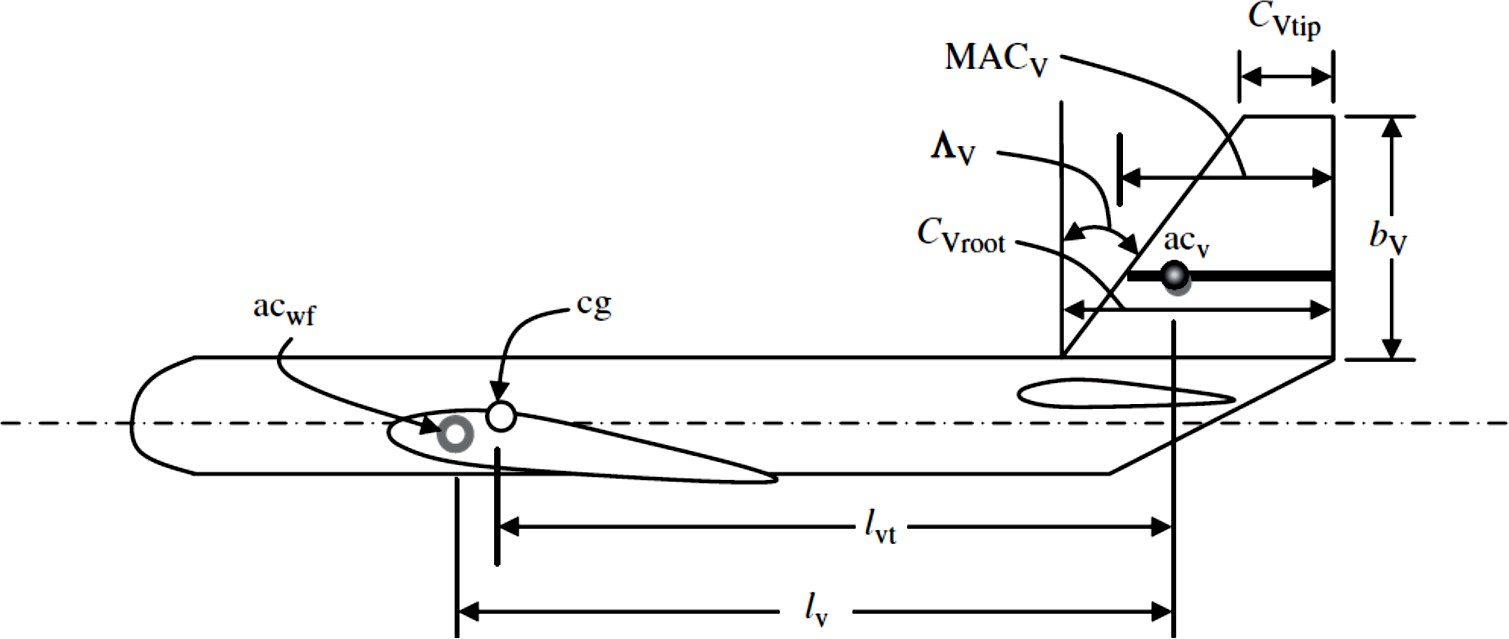
La figure ci-après présente les paramètres types d’un empennage vertical classique.
Figure 2.4 : Paramètres d’empennage vertical (Sadraey, 2012)
L’aire de la surface verticale s’obtient à l’aide de la relation suivante (Sadraey, 2012 ; Raymer, 2006) :
S C
bw Sw
(2.52)
l
VV
V
Avec :
SV la surface totale de l’empennage vertical.
bw l’envergure de l’aile principale.
Sw la surface alaire (surface projetée de l’aile) ;
lV la longueur du bras de levier (longueur entre le quart de corde l’aile principale et le quart
de corde l’empennage vertical).
Larkin (2017) dans ses travaux montre que pour un BWB, la surface verticale est optimale
pour un coefficient de volume CV
0, 0242 et un angle d’inclinaison 22 (Larkin et al,
2017). L’empennage vertical étant une demi-aile, son envergure s’obtient par la relation :
44
1
2
2S AR
VV
Avec :
bV (2.53)
bV l’envergure de l’empennage vertical.
ARV
l’allongement de l’empennage vertical, compris entre 1,3 et 2,0 dans la catégorie d’avion
générale (Raymer, 2006).
La corde moyenne aérodynamique se déduit par la relation suivante :
CV MAC
2bV
ARV
(2.54)
La corde à la racine se déduit de l’équation suivante :
2 1 2
CV
CrV VV
(2.55)
Avec :
31 V
CrV
V
la corde à la racine de l’empennage vertical.
l’effilement de l’empennage vertical, compris entre 0,3 et 0,6 dans la catégorie d’avion
générale (Raymer, 2006).
Connaissant l’effilement et la corde à la racine, la corde à l’extrémité est déduite par l’équation suivante :
CtV
V CrV
(2.56)
En assumant que l’empennage vertical est de forme droite trapézoïdale, l’angle de flèche au bord d’attaque est donné par la relation suivante :
arctan CrV CtV
(2.57)
LE ,V
bv
45
Design du train d’atterrissage
Le train d’atterrissage assure la liaison entre l’avion et le sol ; c’est la composante grâce à laquelle les mouvements de l’avion au sol sont possibles. Ces mouvements comprennent les manœuvres telles que : le taxi dans la zone aéroportuaire, le roulage dans les phases de décollage et d’atterrissage, l’amortissement de l’impact d’atterrissage, le freinage, etc.
Configuration du train d’atterrissage
La plupart des avions commerciaux et de combat utilisent un train d’atterrissage rétractable (dans le fuselage et/ou dans l’aile) de type tricycle (Corke, 2003). Contrairement aux trains d’atterrissage fixes, les trains rétractables présentent l’avantage de diminuer la trainée aérodynamique pendant le vol lorsqu’ils sont escamotés à l’intérieur de l’aéronef.
Dans le cadre de ce travail, le choix du type de train d’atterrissage pour le BWB se fera en s’inspirant des avions historiques à tube et aile (TAW) de taille comparable.
Par ailleurs, le train d’atterrissage doit être convenablement disposé autour du centre de gravité de l’avion, afin que celui-ci soit en équilibre au sol. La figure 2.5 illustre un avion au sol vu de profil. Howe (2000) recommande que les localisations par rapport au centre de gravité des trains avant et arrière soient contraintes par la relation géométrique suivante :
0, 06 lmg
lng lmg 0,15
(2.58)
Où :
lng est la distance entre le train avant et le centre de gravité de l’avion.
lmg
est la distance entre le train arrière et le centre de gravité de l’avion.
46
Figure 2.5 : Positionnement longitudinal du train d’atterrissage par rapport au centre de gravité (Howe, 2000)
Howe (2000) propose de même, dans le plan en élévation, les limites de disposition des trains avant et arrières par rapport à la ligne centrale au sol de l’avion d’une part, et par rapport à la position verticale du centre de gravité d’autre part. Le positionnement du train d’atterrissage de l’avion dans le plan en élévation est donné par la figure 2.6.
Figure 2.6 : Positionnement transversal et vertical du train d’atterrissage par rapport au centre de gravité (Howe, 2000)
47
Dimensionnement des roues du train d’atterrissage
La taille de roue du train d’atterrissage est proportionnelle au poids de l’avion. Spécifiquement, la taille de la roue principale est estimée en assumant que celle-ci supporte 90% du poids total de l’avion (Corke, 2003). Cette estimation est faite en utilisant des formules empiriques basées sur les approximations statistiques de données historiques.
Le diamètre et la largeur de la roue principale se calculent à l’aide de la relation suivant (Corke, 2003) :
Dou w
A W B
(2.59)
Main.WheelMain.Wheelmain
Avec : Wmain 0, 9 WTO
Nwheels
Où :
DMain.Wheel [in] est le diamètre de la roue principale. wMain.Wheel [in] est la largueur de la roue principale. Wmain [lb] est le poids supporté par une roue principale. WTO [lb] est le poids total de l’avion.
Nwheels est le nombre total de roues principales.
Les coefficients A et B dépendent du paramètre calculé (diamètre ou largeur) d’une part, et de la catégorie d’avion d’autre part. Pour un avion de ligne, le calcul du diamètre de la roue
s’effectue avec :
A 1, 630
et B 0,315 . La largeur de la roue qu’en à elle se calcule avec
A 0,104 et
B 0, 480
(Corke, 2003, p.100). Une fois la taille de la roue du train
d’atterrissage principal déterminée, la taille de la roue avant (roue de nez) est déduite. Raymer (2006) préconise que la taille de la roue de nez soit définie au moins à 60% et au plus à 100% de la taille de la roue principale.