Résultats du modèle théorique du comportement du ménage agricole

Résultats du modèle théorique du comportement du ménage agricole

IV- Les résultats du modèle

Afin d’alléger la lecture, nous présentons directement les résultats du modèle. Leur démonstration est disponible au paragraphe V.

Nos résultats sont de plusieurs ordres : un premier résultat formule une contrainte inter temporelle entre les deux périodes (résultat 1).

Un autre ensemble de résultats explicite les conditions d’existence des différents types de main-d’œuvre : celles de la main-d’œuvre salariée permanente sur l’exploitation (résultat 2) et celles de la main-d’œuvre familiale, hors de l’exploitation (résultat 3), et sur l’exploitation (résultat 4).

Le dernier résultat définit le choix optimal du niveau de production sur l’exploitation (résultat 5) et, par déduction, la demande de travail saisonnier.

IV.1 – La contrainte inter temporelle entre les deux périodes (résultat 1)

Notre premier résultat montre que la contrainte inter temporelle entre les deux périodes se traduit de la façon suivante : Résultat 1

(3-10)

L’utilité marginale de la consommation en période de plantation (saison 1), c’est-à-dire l’accroissement de l’utilité qui résulte d’une augmentation marginale de la consommation en période de plantation191, est donc égale à l’utilité marginale espérée de la consommation en période de récolte (saison 2) pondérée par le taux d’actualisation et le taux d’intérêt.

En d’autres termes, le lien entre les utilités marginales des consommations à chacune des deux périodes est fonction du coût du crédit (taux d’intérêt) et de la préférence de l’exploitant pour le présent (taux d’actualisation).

IV.2 – La condition d’existence du travail salarié permanent sur l’exploitation (résultat 2)

Notre deuxième résultat donne la condition d’existence du travail salarié permanent sur l’exploitation :

Résultat 2

La décision d’employer des travailleurs permanents sur l’exploitation  dépend de la condition suivante :

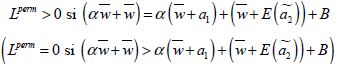(3-11)

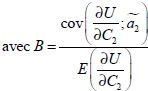
Afin de pouvoir interpréter l’équation (3-11), nous étudions le signe de .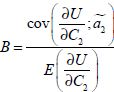

Le signe de B dépend de l’aversion au risque de l’exploitant. En effet, l’utilité est croissante avec la consommation donc  est positif. Le signe de  dépend, quant à lui, de l’aversion au risque de l’exploitant : si l’exploitant est averse au risque son utilité est concave : l’utilité marginale de U par rapport à C2 est décroissante

Si _2 a augmente (toutes choses égales par ailleurs), 2 C se trouve diminuée. Dès lors, comme l’exploitant est averse au risque  augmente.

varient donc dans le même sens en cas d’aversion au risque et  est positif.

Ainsi, lorsque l’exploitant est averse au risque ou riscophobe, B est positif. Par un raisonnement similaire, on trouve que, si l’exploitant est riscophile ou s’il a le goût du risque, B est négatif192.

B représente un coût lié à la prise de risque ou un « coût psychologique » provoqué par la présence conjointe de l’aversion au risque et de l’incertitude sur le coût du travail saisonnier [Eeckhoudt et Gollier, 1992] (p.169).

Il est positif lorsque l’exploitant est averse au risque (ou riscophobe) et négatif lorsque celui-ci est riscophile, c’est-à-dire lorsqu’il a le goût du risque. En cas de neutralité au risque, ce coût est nul.

Nous interprétons dans un premier temps l’équation (3-11), lorsque l’exploitant est neutre au risque : B=0. Dans ce cas, l’exploitant recourt à des travailleurs permanents plutôt qu’à des travailleurs saisonniers ou familiaux si le coût d’un permanent sur l’ensemble du cycle de production (l’ensemble des deux périodes)  est égal à la somme du coût d’un saisonnier sur la période de plantation (saison 1) , de son coût espéré à la période de récolte (saison 2) .

En d’autres termes, lorsque l’exploitant est neutre au risque, l’exploitant emploie des travailleurs permanents si leur coût sur l’ensemble du cycle de production est égal au coût anticipé des saisonniers sur l’ensemble du cycle de production.

Si, au contraire, le coût des permanents sur les deux périodes est supérieur au coût anticipé des saisonniers sur l’ensemble du cycle de production, l’exploitant n’emploie pas de travailleurs permanents.

Ainsi, l’augmentation du coût espéré des travailleurs salariés saisonniers accroît la probabilité d’emploi de travailleurs permanents.

Les exploitants agricoles sont généralement averses au risque (voir par exemple [Binswanger, 1980 ; Groom et al., 2008 ; Koundouri et al., 2009]). L’introduction de l’aversion au risque fait apparaître un terme B positif lié à l’aléa sur le coût du travail saisonnier.

La présence simultanée de l’incertitude et de l’aversion au risque conduit à ajouter au coût des travailleurs saisonniers un coût psychologique positif mesuré par .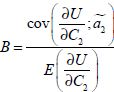

Ainsi, dans le cas classique d’un exploitant riscophobe, le coût anticipé du travail saisonnier est majoré par le coût psychologique lié à l’aléa qui porte sur le coût du travail saisonnier. L’aversion au risque de l’exploitant rend dès lors plus probable l’emploi de travailleurs permanents.

Ce résultat original montre que l’emploi permanent joue un rôle assurantiel ( ex ante) par rapport à l’aléa sur le coût du travail saisonnier .

IV.3 – Les conditions d’existence du travail familial hors et sur de l’exploitation (résultats 3 et 4)

Notre troisième groupe de résultats concernent le travail familial. Nous notons 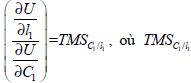 est le taux marginal de substitution de la consommation en période 1 au loisir en période 1. En d’autres termes,  représente l’accroissement marginal de la consommation en période 1 dont le ménage doit disposer pour compenser une réduction marginale de son loisir à la même période, l’utilité étant maintenue constante.

De la même manière 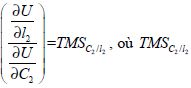 est le taux marginal de substitution de la consommation en période 2 au loisir en période 2.

Le résultat 3 donne les conditions d’existence du travail familial hors de l’exploitation : Résultat 3

En période de plantation (saison 1), la famille travaille hors de l’exploitation  si :

(3-12)

De la même manière, en période de récolte (saison 2), la famille travaille hors de l’exploitation  si :

(3-13)

L’offre de travail familial hors de l’exploitation dépend donc du salaire extérieur (wo ) .

À chaque période, s’il y a égalité entre le taux marginal de substitution de la consommation au loisir de la période considérée et le salaire reçu hors de l’exploitation, le ménage travaille hors de l’exploitation.

Par contre, si la quantité additionnelle de revenu dont le ménage doit disposer pour être prêt à diminuer d’une unité sa consommation de loisir (l’utilité du ménage étant maintenue constante) est supérieure au revenu qu’il peut recevoir pour une heure de travail hors de l’exploitation, le ménage ne travaille pas hors de l’exploitation.

L’augmentation du niveau de salaire reçu hors de l’exploitation accroît la probabilité d’emploi de la famille à l’extérieur de l’exploitation.

La règle de décision est la même sur les deux périodes cependant, le comportement de la famille dans sa décision de travailler hors de l’exploitation peut changer d’une période à l’autre, les taux marginaux de substitution de la consommation au loisir de chacune des périodes pouvant être différents.

Ce résultat est un résultat classique des modèles de ménages agricoles [Benjamin, 1996].

Le résultat 4 donne les conditions d’existence du travail familial sur l’exploitation : Résultat 4

En période de plantation (saison 1), la famille travaille sur l’exploitation  si :

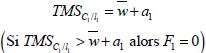
En période de plantation (saison 1), la famille travaille sur l’exploitation  si :

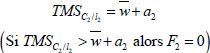
À chaque période, l’offre de travail familial sur l’exploitation dépend du coût du travail saisonnier réalisé à la période en question (w ai ) .

S’il y a égalité entre le taux marginal de substitution de la consommation au loisir pour une période et le salaire des travailleurs saisonniers sur cette même période, le ménage travaille sur l’exploitation.

En revanche, si la quantité additionnelle de revenu dont le ménage doit disposer pour être prêt à diminuer d’une unité sa consommation de loisir (l’utilité du ménage étant maintenue constante) est supérieure au salaire du travail salarié saisonnier sur la période concernée, le ménage ne travaille pas sur l’exploitation.

L’accroissement du niveau de salaire des saisonniers accroît la probabilité d’emploi de la famille sur l’exploitation.

On notera que le coût du travail saisonnier dans les équations (3-14) et (3-15) n’est pas aléatoire. L’arbitrage se fait donc en fonction du coût du travail saisonnier réalisé à chaque période et non pas en fonction de l’espérance du coût aléatoire du travail saisonnier comme c’est le cas pour le travail salarié permanent.

Alors que le travail permanent joue un rôle d’assurance ex post par rapport à l’aléa sur le coût du travail saisonnier, le travail familial joue, quant à lui, un rôle d’ajustement ex post.

L’arbitrage de l’offre de travail de la famille, sur et hors de l’exploitation, dépend donc conjointement du coût du travail salarié saisonnier effectif ou réalisé à chacune des périodes et de la rémunération que les membres de la famille peuvent obtenir pour leurs activités non agricoles.

IV.4 – Le choix optimal du niveau de production (résultat 5)

Notre dernier résultat explicite la demande de travail sur l’exploitation : Résultat 5

Le choix optimal193 de L1 et donc de Q se caractérise par :

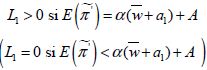(3-16)

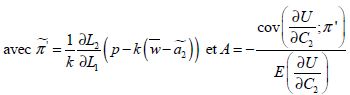
De manière analogue au raisonnement que nous avons fait précédemment et afin de pouvoir interpréter l’équation (3-16), nous étudions, dans un premier temps, le signe de 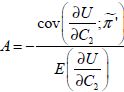 puis, dans un second temps, nous explicitons ce que représente  et .

Le signe de 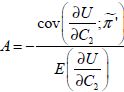 dépend, là encore, de l’aversion au risque de l’exploitant.

En effet, comme l’utilité est croissante avec la consommation,  est positif. Le signe  dépend, quant à lui, de l’aversion au risque de l’exploitant.

En effet, si l’exploitant est averse au risque, son utilité est concave : l’utilité marginale de U par rapport à C2 est décroissante (). Si  augmente (toutes choses égales par ailleurs), C2 se trouve amélioré. Dès lors, comme l’exploitant est averse au risque  diminue.

varient donc en sens inverse en cas d’aversion au risque. On peut donc dire que  est négatif. Ainsi, lorsque l’exploitant est averse au risque A est positif

De manière analogue, lorsque l’exploitant a le goût du risque, on peut montrer que A est négatif194.

Comme précédemment, A représente un coût lié à la prise de risque ou un « coût psychologique » provoqué par la présence conjointe de l’aversion au risque et de l’incertitude sur le coût du travail saisonnier [Eeckhoudt et Gollier, 1992] (p.169).

Il est positif lorsque l’exploitant est averse au risque et négatif lorsque celui-ci a le goût du risque. En cas de neutralité au risque, ce coût est nul.

Le terme de covariance représente la perte d’espérance d’utilité liée à l’accroissement du risque.

Nous explicitons maintenant ce que représente .

 représente l’accroissement du travail de récolte L2 qui résulte d’un accroissement marginal du travail de plantation L1.

représente le bénéfice marginal du travail de récolte (saison 2). On notera cependant que c’est le coût du travail saisonnier  qui est pris en compte.

En effet, comme nous l’avons vu dans l’ensemble des résultats précédents, les arbitrages de la demande de travail sur l’exploitation se font en fonction du coût du travail salarié saisonnier. Celui-ci est en effet central dans la détermination des conditions d’existence des permanents (voir résultat 2) et de la famille (voir résultat 4).

 correspond donc à la productivité marginale du surplus de travail de récolte qui découle d’un accroissement du travail de plantation.

 représente le coût marginal d’un travailleur saisonnier en période de plantation195.

191 Les autres arguments de la fonction d’utilité étant maintenus constants.

192 Si l’exploitant a le goût du risque .

193 Comme nous avons considéré que le marché du travail permanent était parfait, l’exploitant peut toujours trouver la main-d’œuvre nécessaire au travail de récolte même si le coût du travail saisonnier est infini.

194 Si l’exploitant a le goût du risque : A est négatif.

195 L’exploitant a dû emprunter en période de plantation (saison 1) pour payer les travailleurs.

Ainsi, d’après l’équation (3-16), à l’optimum, la productivité marginale espérée du travail de récolte est égale au coût du travail salarié saisonnier de plantation plus un terme dont le signe dépend de l’aversion au risque de l’exploitant.

En d’autres termes, lorsque l’exploitant est neutre au risque (A =0), son espérance de bénéfice en période de récolte doit compenser ce qui lui en a coûté de planter à la saison précédente.

L’introduction de l’aversion au risque fait apparaître un terme A lié à l’aléa sur le coût du travail saisonnier. La présence simultanée de l’incertitude et de l’aversion au risque conduit en effet à ajouter au coût de plantation un coût psychologique positif mesuré par .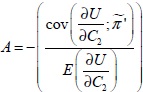

On retrouve ici un résultat de l’étude de la décision de production en contexte d’incertitude : le risque relatif au prix d’un facteur de production réduit le niveau de production choisi par un décideur riscophobe [Eeckhoudt et Gollier, 1992].

IV.5 – Synthèse et conclusions du modèle théorique

Notre proposition théorique permet de considérer la demande de travail salarié dans une exploitation agricole en distinguant le travail salarié permanent et le travail salarié saisonnier.

Le cadre théorique du modèle de ménage agricole permet d’intégrer la double nature des ménages agricoles producteurs-consommateurs et autorise la dépendance entre l’implication de la main-d’œuvre familiale sur l’exploitation et la décision d’employer une main-d’œuvre salariée.

Notre modèle est un modèle en deux périodes qui tient compte de la saisonnalité de l’activité agricole. Il distingue le travail salarié selon la durée du contrat et selon le coût de recrutement : le coût des travailleurs permanents, employés sur les deux périodes, est fixe et exogène.

Le coût des travailleurs saisonniers, employés sur une seule période, est quant à lui aléatoire : le salaire des travailleurs est en effet majoré d’un coût de recrutement aléatoire.

Le Tableau 43 résume les différents arbitrages des décisions d’offre de travail de la famille et de demande de travail salarié, permanent et saisonnier, sur l’exploitation. Nos résultats montrent que le coût du travail salarié saisonnier, sur lequel porte l’aléa, est central dans l’ensemble de ces arbitrages.

La décision d’emploi de travailleurs permanents en période de plantation est prise en fonction du coût anticipé des travailleurs saisonniers en période de récolte et de l’aversion au risque de l’exploitant.

La décision de travail de la famille sur l’exploitation dépend, quant à elle, non pas du coût anticipé des travailleurs saisonniers mais de leur coût effectif ou réalisé à chacune des périodes.

Ainsi, les travailleurs permanents jouent un rôle d’assurance ex ante par rapport à l’incertitude sur le coût des saisonniers.

La famille joue, quant-à elle, un rôle d’adaptation ex post en fonction en fonction de la réalisation du coût du travail saisonnier ( a ).

L’emploi de permanent dans un but assurantiel crée ce que P. Bardhan [1983] appelle un coût de thésaurisation. L’exploitant arbitre donc entre le coût de thésaurisation et le coût de recrutement de la main-d’œuvre salariée.

Dans un modèle de ménage agricole classique comme, par exemple, celui exposé par C. Benjamin [1996], les décisions d’offre de travail de la famille et de demande de travail salarié sont en partie reliées au coût du travail salarié et au salaire que peut recevoir la famille hors de l’exploitation.

Dans notre modèle, ces arbitrages se trouvent modifiés par l’introduction d’un coût de recrutement différencié selon les travailleurs salariés et l’introduction d’un aléa portant sur ce coût. Les décisions du ménage en termes d’offre de travail intègrent désormais ce coût.

Selon l’aversion au risque de l’exploitant et le coût du travail salarié saisonnier, la gestion de l’aléa se fait soit ex ante par le recrutement de travailleurs permanents, soit ex post par la mobilisation de la main-d’œuvre familiale.

Ainsi, la distinction du travail salarié selon la durée du contrat et le coût de recrutement au sein d’un modèle de ménage agricole permet de mettre en évidence que, même dans une exploitation familiale, l’arbitrage entre la main-d’œuvre salariée permanente et la main- d’œuvre salariée saisonnière ne reflète pas uniquement la saisonnalité de l’activité.

Il repose sur un arbitrage entre coût de thésaurisation et coût de recrutement, la main-d’œuvre familiale jouant un rôle d’ajustement ex post .

Tableau 43- Résumé des conditions d’existence des différents types de travail sur l’exploitation

V- Démonstration des résultats

V.1 – Optimisation en période de récolte (saison 2)

Le programme de maximisation en période de récolte (saison 2) s’écrit :

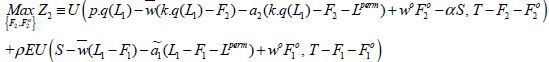
sous les contraintes

(3-17)

Les conditions de premier ordre sont :

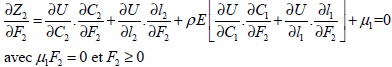(3-18)

étant le multiplicateur de Lagrange associé à la contrainte

(3-19)

Avec

étant le multiplicateur de Lagrange associé à la contrainte

Elles s’écrivent aussi de la façon suivante :

(3-20)

Et

(3-21)

Nous notons 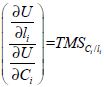, où TMS Ci /li est le taux marginal de substitution de la consommation en période i = {1,2} au loisir en période i = {1,2}.

D’après l’équation (3-20) et selon la saturation des contraintes de positivité, on trouve que (résultat 4) :

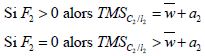
D’après l’équation (3-21) et selon la saturation des contraintes de positivité, on trouve que (résultat 3) :

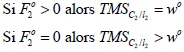
V.2 – Optimisation en période de plantation (saison 1)

Le programme de maximisation en période de plantation (saison 1) s’écrit :

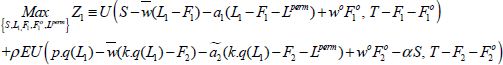
sous les contraintes

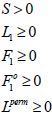
Les conditions de premier ordre sont :

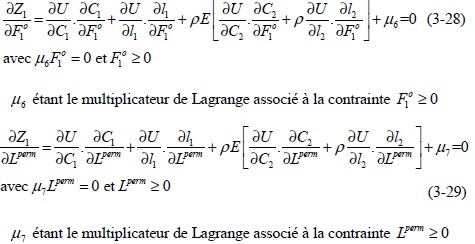
Elles s’écrivent aussi de la façon suivante :

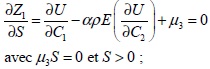(3-30)

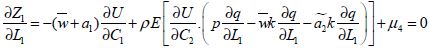(3-31)

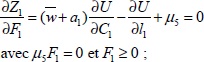(3-32)

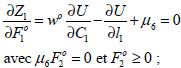(3-33)

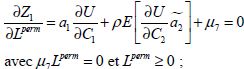(3-34)

D’après l’équation (3-30), on trouve que (résultat 1) :

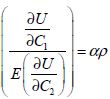(3-35)

D’après l’équation (3-32) et selon la saturation des contraintes de positivité, on trouve que (résultat 4) :

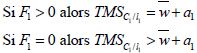(3-36)

D’après l’équation (3-33) et selon la saturation des contraintes de positivité, on trouve que (résultat 3) :

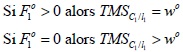(3-37)

D’après l’équation (3-31) et selon la saturation des contraintes de positivité, on a (démonstration du résultat 5):

En définissant , l’équation (3-38) équivaut à :

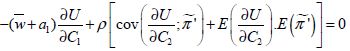(3-39)

Soit :

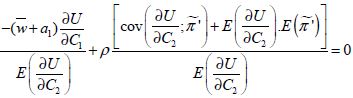(3-40)

D’après le résultat 1 (équation (3-35)), on peut écrire :

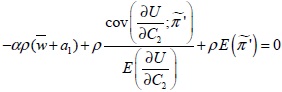(3-41)

Soit :

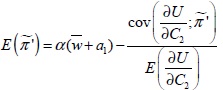(3-42)

Ou encore

si (résultat 5):

(3-43)

avec :

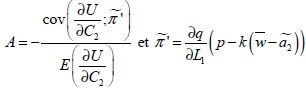
Comme

s’écrit aussi :

(3-44)

D’après l’équation (3-34) et selon la saturation des contraintes de positivité, on a (démonstration du résultat 2):

(3-45)

ou si :

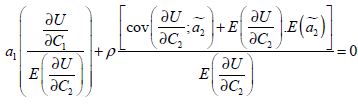
Soit, d’après le résultat 1 (équation (3-35)), si :

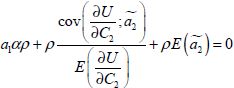(3-47)

Ou encore si :

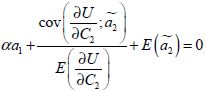(3-48)

En additionnant de part et d’autre de l’équation , l’équation (3-48) équivaut à :

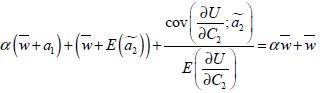(3-49)

Ou encore

si (résultat 2):

(3-50)

avec :

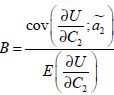
(3-51)