Modélisation économétrique des décisions, Exploitations agricoles
II- Modèle économétrique et méthodologie d’estimation
La modélisation économétrique des décisions de travail sur les exploitations agricoles familiales a progressivement évolué. L’étude des décisions de travail d’un seul membre de la famille s’est généralement appuyée sur l’estimation de probits simples (voir par exemple [Sumner, 1982]).
Les applications empiriques sur les décisions de travail du chef d’exploitation et de son conjoint ont généralement été faites à partir de l’estimation de probits bivariés (voir par exemple [Huffman et Lange, 1989 ; Lass et Gempesaw, 1992]).
Cette modélisation a été remise en question (voir [Benjamin et Kimhi, 2006]) et la prise en compte simultanée de plusieurs types de main-d’œuvre a nécessité le développement d’une stratégie nouvelle.
L’approche développée notamment par C. Benjamin, A. Corsi et H. Guyomard [1996] se fonde sur la maximisation d’utilité indirecte. Dans cette approche, des régimes de travail sont définis comme les combinaisons des résultats de toutes les équations de participations des différents types de main-d’œuvre étudiés.
Une mesure de l’utilité indirecte propre à chaque régime peut être spécifiée. Le ménage choisit le régime qui lui fournit la plus grande utilité indirecte.
Un modèle probabiliste est obtenu en ajoutant, pour chaque régime, un terme d’erreur additif à la mesure d’utilité indirecte déterministe. Le travail présenté ici s’appuie sur cette stratégie d’estimation.
II.1 – Les régimes de travail considérés
Dans le modèle théorique que nous avons exposé dans le chapitre précédent, nous avons considéré que l’exploitant décide simultanément de l’emploi des trois différents types de main-d’œuvre : la main-d’œuvre familiale, la main-d’œuvre salariée permanente et la main- d’œuvre salariée saisonnière.
Ce modèle nous a permis de faire émerger les conditions d’existence de chacune de ces catégories de main-d’œuvre sur l’exploitation.
Il existe plusieurs combinaisons possibles de ces catégories que nous appelons donc, dans le prolongement des travaux précédents [Benjamin et al., 1996 ; Benjamin et Kimhi, 2006 ; Blanc et al., 2008], des régimes de travail.
Un régime de travail est une combinaison spécifique de différents types de travail sur une exploitation. Les régimes de travail que nous considérons sont présentés dans le Tableau 45.
Afin de faciliter la lecture des régimes, nous les numérotons par un nombre de trois chiffres, chacun des chiffres représentant l’absence (0) ou la présence (1) d’un type de main-d’œuvre.
Le premier chiffre représente la main-d’œuvre familiale, le deuxième la main-d’œuvre permanente et le troisième la main-d’œuvre saisonnière.
Tableau 45- Présentation des régimes de travail
| Travail familial sur l’exploitation198 | Travail salarié permanent sur l’exploitation | Travail salarié saisonnier sur l’exploitation | Régime |
| Non | Non | Non | 000 |
| Non | Non | Oui | 001 |
| Non | Oui | Non | 010 |
| Non | Oui | Oui | 011 |
| Oui | Non | Non | (Régime de référence) 100 |
| Oui | Non | Oui | 101 |
| Oui | Oui | Non | 110 |
| Oui | Oui | Oui | 111 |
À la différence des autres travaux empiriques, nous ne voulons pas nous limiter à l’étude de l’offre de travail de l’exploitant ou à celle du couple (exploitant et conjoint)199.
Nous souhaitons prendre en compte l’offre de travail de la famille dans son ensemble que nous définissons comme l’offre de travail de l’ensemble de membres de la famille200 en âge de travailler, c’est-à-dire ayant entre 15 et 70 ans.
L’hypothèse d’une fonction d’utilité unique pour la famille est maintenue et le travail des membres de la famille est agrégé.
Dans le secteur que nous étudions, la plupart des exploitants (et co-exploitants) travaille uniquement sur son exploitation. Ils sont rarement pluri-actifs201.
198 Membres de la famille ayant entre 15 et 70 ans et différents de l’exploitant et des co-exploitants (l’exploitant est la personne physique qui assure la gestion courante et quotidienne de l’exploitation et prend les décisions au jour le jour. Par convention, on ne retient qu’une seule personne comme exploitant : celle qui assure la plus grande part de responsabilité. Les autres personnes qui participent à la gestion courante sont des co-exploitants dans le cas des formes sociétaires -GAEC, SCEA…-).
199 À notre connaissance, seul Blanc et al. [2008] prennent en compte le travail de la famille dans son ensemble. Ils ne précisent cependant pas quels travailleurs sont exactement considérés.
200 Vivant sur l’exploitation ou y travaillant de manière régulière.
201 85% des exploitants de la sous-population que nous étudions travaille à plein temps sur son exploitation et n’a aucune activité extérieure.
De plus, le nombre d’exploitations avec des co-exploitants est relativement faible202. Dès lors, nous ne nous intéressons pas à l’offre de travail des exploitants et co-exploitants mais uniquement à celle des autres membres de la famille en âge de travailler.
Nous prendrons cependant en compte, dans notre estimation, d’une part les caractéristiques du chef d’exploitation qui, comme l’ont montré les travaux antérieurs, influencent la demande de travail salarié [Huffman et Lange, 1989 ; Lass et Gempesaw, 1992 ; Findeis et Lass, 1994 ; Benjamin et al., 1996 ; Benjamin et Kimhi, 2006 ; Blanc et al., 2008] et, d’autre part, la présence ou non de co-exploitants afin que nos résultats ne soient pas biaisés.
Étant donné que, dans les exploitations que nous étudions, moins de 3% des conjoints sont des co-exploitants, le travail des conjoints est pris en compte dans le travail familial que nous considérons.
Enfin, comme le montre le Tableau 45, outre le travail salarié, permanent et saisonnier, seule l’offre de travail de la famille sur l’exploitation intervient dans la définition des régimes de travail.
Nous ne considérons pas directement l’offre de travail de la famille hors de l’exploitation afin de ne pas multiplier les régimes de travail. Cependant, comme nous le verrons par la suite, l’offre de travail de la famille hors de l’exploitation est sous-entendue dans l’analyse.

Ainsi, bien que nos régimes de travail ne permettent pas de tenir compte des interactions entre les décisions de travail de chacun de membres de la famille, ils permettent, pour la première fois, de considérer les interactions entre l’ensemble de la main-d’œuvre familiale en âge de travailler, la main-d’œuvre salariée permanente et la main-d’œuvre salariée saisonnière.
Nos régimes de travail ainsi définis, nous estimons la probabilité pour une exploitation d’appartenir à chacun de ces régimes de travail afin de mettre en évidence les déterminants des décisions de travail des exploitations agricoles familiales et les complémentarités et les substitutions entre les différents types de main-d’œuvre.
II.2 – Le choix du logit multinomial et ses hypothèses
Nous cherchons donc à estimer la probabilité pour une exploitation d’appartenir à un régime de travail spécifique.
L’exploitant (ou le ménage203) choisit donc un régime de travail parmi huit combinaisons possibles que nous avons présentées précédemment (voir Tableau 45). Les différents régimes de travail sont non ordonnés.
L’exploitant ![]() choisit le régime de travail
choisit le régime de travail ![]() qui maximise son utilité indirecte
qui maximise son utilité indirecte ![]() .
.
Pour chaque régime j, l’utilité indirecte se décompose en une part déterminée par un ensemble de caractéristiques X k et en une part stochastique jk :
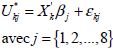
X k est le vecteur des caractéristiques de l’exploitant k et de sa famille ainsi que les caractéristiques de l’exploitation et de sa localisation. j est le vecteur de l’ensemble des coefficients et de la constante.
Soit une variable Vkj qui correspond au choix de l’exploitant parmi les j=8 choix alternatifs.
Soit une variable Vkj qui correspond au choix de l’exploitant parmi les j=8 choix alternatifs.
Vkj prend la valeur 1 lorsqu’une exploitation k appartient au régime j et 0 sinon (c’est-à-dire s’il appartient à un régime i avec i j ).
Le choix de l’exploitant s’écrit :
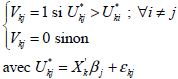
Ou encore :
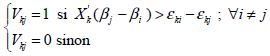 (4-3)
(4-3)
La probabilité d’occurrence de chacun des choix peut être analysée par le biais d’un modèle logit multinomial, le modèle à choix multiples « le plus pratique et le plus fréquemment utilisé » [Greene, 2005] (p. 710-711).
Dans le cas d’un logit multinomial, les erreurs sont indépendantes et identiquement distribuées (iid) selon une loi de Weibull.
Le caractère non biaisé des coefficients estimés par un tel modèle repose sur l’hypothèse de l’indépendance des solutions non pertinentes (Independance of Irrelevant Alternatives, IIA) (voir Encadré 5).
La probabilité du jème choix s’écrit alors [Greene, 2005] (p.706-707) :
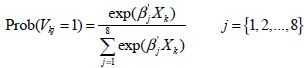 (4-4)
(4-4)
X k correspond au vecteur des variables explicatives (caractéristiques de l’exploitant, de la famille, de l’exploitation et de la localisation), j au vecteur de l’ensemble des coefficients pour le régime j (effet de X k sur la probabilité du choix j) et de la constante.
Ainsi :
![]() (4-5)
(4-5)
Un des régimes est alors considéré comme régime de référence : ses coefficients sont contraints à zéro.
Dans notre cas, nous considérons que le régime purement familial (100), c’est-à-dire le régime ou l’exploitant travaille uniquement avec sa famille sans employer de salariés permanents ni de salariés saisonniers, est le régime de référence.
Dès lors, la probabilité d’occurrence des sept autres régimes s’écrit :
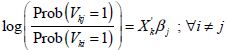
avec le régime i comme régime de référence (dans notre cas régime 100 ![]() (4-6)
(4-6)
Du fait de la non-linéarité du modèle logit multinomial, l’interprétation de l’effet des variables explicatives est plus complexe que dans le cas d’une régression linéaire.
Les coefficients de l’estimation d’un logit multinomial correspondent à l’effet d’un changement d’une variable explicative sur la probabilité d’un choix j par rapport à celle d’un choix i (choix de référence), les autres variables explicatives étant maintenues constantes. Ces coefficients sont difficiles à interpréter directement.
Pour faciliter l’interprétation, les effets d’un changement marginal (ou discret) des variables explicatives sur la probabilité d’adoption du jème régime sont généralement calculés en un point de référence204. Le calcul se fait souvent au niveau moyen des différentes variables explicatives.
202 Moins de 8% des exploitations de la sous-population que nous étudions.
203 Puisque nous considérons un ménage unitaire.
204 À l’inverse des effets marginaux dans les modèles linéaires, les effets marginaux dans un logit multinomial ne sont pas constants. Ils dépendent de la position où l’on choisit de les calculer, c’est à dire de la valeur des coefficients et des variables.
L’effet marginal s’écrit :
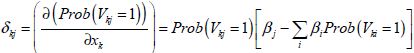 (4-7)
(4-7)
Étant donné que notre modèle comporte un certain nombre de variables discrètes, nous utilisons la commande STATA Margeff pour estimer les effets marginaux. Cette commande calcule la moyenne des effets marginaux individuels plutôt que les effets marginaux au point moyen [Bartus, 2005].
Encadré 5- L’hypothèse de l’indépendance des solutions non pertinentes (Independance of Irrelevant Alternatives, IIA)
Le caractère non biaisé des coefficients estimés par un modèle logit multinomial repose sur l’hypothèse de l’indépendance des solutions non pertinentes, c’est à dire sur l’hypothèse que les probabilités des différents choix alternatifs sont indépendantes les unes des autres.
Cette hypothèse implique que l’addition ou le retrait d’une alternative n’affecte pas la probabilité des autres alternatives. Par exemple, si A est préféré à B dans l’ensemble [A,B], l’introduction d’une troisième alternative C, transformant l’ensemble des choix en [A,B,C], ne doit pas modifier le choix entre les deux alternatives A et B.
L’exemple le plus courant, proposé par McFadden [1974], est celui des bus rouge et bleu : considérons une personne qui choisit son mode de transport entre une voiture et un bus rouge et que son choix entre ces deux options est équiprobable (la probabilité de chacun des choix est de 0,5).
En considérant que la personne n’est pas sensible à la couleur du bus, l’introduction d’un troisième mode de transport dans l’ensemble des choix, un bus bleu, conduit aux probabilités suivantes : 0,5 pour la voiture, 0,25 pour le bus rouge et 0,25 pour le bus bleu.
Si l’hypothèse des IIA était vérifiée, le choix entre la voiture et le bus rouge devrait rester équiprobable malgré l’introduction de la troisième alternative (0,33 pour la voiture, 0,33 pour le bus rouge et 0,33 pour le bus bleu par exemple). La proximité du choix entre le bus bleu et le bus rouge conduit à la violation de l’hypothèse des IIA.
Le test de Hausman [Hausman et McFadden, 1984 ; Small et Hsiao, 1985] permet d’infirmer ou de confirmer l’hypothèse des IIA en comparant la variation des coefficients lors du retrait ou de l’ajout d’alternatives.
Dans notre cas, les résultats de ces tests ne sont pas concluants, le retrait de certaines alternatives semblant en effet changer sensiblement les coefficients estimés.
Nous maintenons cependant l’estimation par le biais d’un logit multinomial et ce pour plusieurs raisons. D’une part, le test d’Hausman est fortement remis en question [Long et Freese, 2006 ; Cheng et Long, 2007].
En effet, ces tests « donnent des résultats contradictoires » [Long et Freese, 2006] (p.244) et « rejettent souvent l’hypothèse quand les alternatives paraissent distinctes et échouent souvent à invalider les IIA quand les alternatives peuvent raisonnablement être considérées comme proches substituts » [Cheng et Long, 2007] (p.583).
D’autre part, en cas de violation des IIA, deux alternatives sont souvent proposées : l’estimation par le biais d’un logit emboîté (ou nested logit) et le probit multinomial.
L’estimation par le biais d’un logit emboîté nécessite de disposer des attributs des choix, c’est à dire des caractéristiques liées au choix et propres à chaque individu. Dans le cas que nous étudions, il n’existe pas de caractéristiques des régimes propres à chaque individu.
Le probit multinomial est une autre méthode d’estimation qui relâche l’hypothèse des IIA. Cette estimation est cependant très exigeante en calcul et n’est pas utilisable lorsque plus de cinq alternatives sont considérée.
De plus, certains récents travaux ont montré que, quand bien même l’hypothèse des IIA est violée, le logit multinomial continue de fournir des résultats plus satisfaisants que le probit multinomial [Kropko, 2008].
II.3 – L’interprétation de la substitution et de la complémentarité
Les résultats d’un logit multinomial ne permettent pas de mettre directement en évidence des effets de substitution et de complémentarité. Comme cela a été fait dans les travaux précédents [Benjamin et al., 1996 ; Benjamin et Kimhi, 2006 ; Blanc et al., 2008], nous interprétons les effets de substitution et complémentarité de manière indirecte.
Nous considérons que lorsqu’une même variable a un effet similaire sur deux types de main- d’œuvre (ou sur les régimes avec ces deux types de main-d’œuvre), ces deux types de main- d’œuvre sont complémentaires. Lorsqu’elle a un effet opposé, les deux types de main- d’œuvre sont substituables.
Ainsi, pour C. Benjamin, A. Corsi et H. Guyomard [1996], si le niveau de formation générale de l’épouse accroît la probabilité d’être dans les régimes où la femme travaille à l’extérieur de l’exploitation et simultanément celles des régimes où il existe du travail salarié sur l’exploitation, ce résultat suggère que le travail salarié est substitut au travail de la femme sur l’exploitation.
Dans notre cas, si une variable influence positivement la probabilité des régimes avec travailleurs salariés et négativement (respectivement positivement) la probabilité des régimes avec travailleurs permanents, nous dirons que, par rapport à cette variable, ces deux types de travail sont substituts (respectivement complémentaires).
Par exemple, il est possible de considérer que l’élasticité du travail ( Lsais ) par rapport au travail permanent ( Lperm ), c’est-à-dire la variation de la quantité de travail saisonnier qui résulte de l’accroissement de la quantité de travail permanent, est du même signe que le rapport des élasticités de ces deux types de travail par rapport à une variable commune ( X i ).
En d’autres termes :
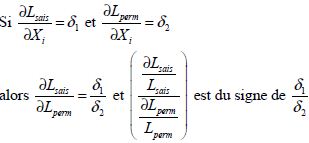 (4-8)
(4-8)
