5. Analyse multi variée
Lors de l’analyse bi variée, nous avons remarqué du point de vue statistique que le taux de marge nette était la variable la plus corrélée avec la rentabilité financière pour toutes les banques commerciales sous étude.
Etant donné que la corrélation n’est pas forcement causalité, nous allons vérifier s’il existe une relation de cause à effet pouvant expliquer significativement la variabilité de la rentabilité financière des banques commerciales en RDC.
Rappelons que nos panels sont totalement hétérogènes (Voir Résultats des Tests de Hsiao) et selon la théorie économétrique, il est recommandé de procéder par des estimations équation par équation. (Bourbonnais R. , 2015) en estimant les paramètres en fonction de chaque individu statistique.
Cependant, nous avons identifié la présence d’une multicolinéarité entre les variables explicatives dans 8 banques17. Un effet masque est une forte menace pour l’atteinte de notre objectif de recherche (Identification de la variable la plus significative partant du modèle de Dupont).
L’un des remèdes proposé par la littérature économétrique est de combiner les séries en coupes transversales et séries temporelles; donc, opter pour l’estimation en panel. (Bosonga, 2017).
Donc, pour ces raisons, nous allons revenir à une estimation en panel mais en supposant que les deux panels des banques sont partiellement homogènes; c’est-à-dire que seuls les coefficients sont les mêmes; et que la seule différence réside au niveau des constantes.
Il s’agit donc d’un modèle à effet individuel.
𝑅𝑂𝐸𝑖𝑡 = 𝜶𝟎𝒊 + 𝜷𝒊 𝑋𝑖𝑡 + 𝜀𝑖𝑡
Avec (𝛼0𝑖 ≠ 𝛼0 ) et (𝛽𝑖 = 𝛽) ∀𝑖 de tous les deux panels (Panel des banques locales et Panel des banques étrangères).
Pour identifier la variable la plus significative à partir du modèle théorique de Dupont, nous allons estimer pour chaque panel des banques, un modèle à effet fixe; un modèle à effet aléatoire, le test de spécification de Hausman ainsi que les tests post-estimations pour s’assurer que les hypothèses stochastiques et structurelles suivantes sont respectées :
𝑢
𝑢
𝐸 ~ (0, 𝜎2 𝐼); Le vecteur des résidus est normalement distribué
𝑡
𝑡
(𝜀2 ) = 𝜎2𝜀; la variance de l’erreur est constante pour tous les exercices comptables et pour toutes les banques : Homoscédasticité.
(𝜀𝑡𝜀𝑡′) = 0, ∀𝑡 ≠ 𝑡′; il existe une absence d’autocorrélation des erreurs d’un exercice à un autre.
𝐶𝑜𝑣 (𝜀𝑡, 𝑥 ) = 0; L’erreur n’est pas corrélée avec les variables explicatives. C’est l’hypothèse d’endogénéité de la variable 𝑥 . (Bosonga, 2017)
n > k+1; le nombre d’observations est supérieur au nombre des paramètres à estimer.
5.1. Banques locales
5.1.1. Estimation du modèle à effet fixe et aléatoire
| Modèle individuel à effet fixe | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| DRCOM | 0.077648 | 0.017915 | 4.334196 | 0.0003 |
| DROT | 1.024405 | 0.605476 | 1.691899 | 0.1055 |
| DCFP | 0.01624 | 0.014848 | 1.093735 | 0.2865 |
| C | -0.005666 | 0.01288 | -0.439898 | 0.6645 |
| Effects Specification | ||||
| Cross-section fixed (dummy variables) | ||||
| R-squared | 0.530763 | Mean dependent var | 0.005597 | |
| Adjusted R-squared | 0.396695 | S.D. dependent var | 0.081619 | |
| S.E. of regression | 0.063396 | Akaike info criterion | -2.466521 | |
| Sum squared resid | 0.0844 | Schwarz criterion | -2.13347 | |
| Log likelihood | 41.53129 | Hannan-Quinn criter. | -2.364704 | |
| F-statistic | 3.958915 | Durbin-Watson stat | 2.116339 | |
| Prob(F-statistic) | 0.00836 |
| Modèle individuel à effet aléatoire | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | -0.004914 | 0.012637 | -0.388878 | 0.7008 |
| DRCOM | 0.075442 | 0.016119 | 4.680429 | 0.0001 |
| DROT | 0.934179 | 0.511008 | 1.828111 | 0.08 |
| DCFP | 0.014662 | 0.013959 | 1.05039 | 0.304 |
| Effects Specification | ||||
| S.D. | Rho | |||
| Cross-section random | 0.000000 | 0 | ||
| Idiosyncratic random | 0.063396 | 1 | ||
| Weighted Statistics | ||||
| R-squared | 0.520907 | Mean dependent var | 0.005597 | |
| Adjusted R-squared | 0.461021 | S.D. dependent var | 0.081619 | |
| S.E. of regression | 0.059921 | Sum squared resid | 0.086172 | |
| F-statistic | 8.698236 | Durbin-Watson stat | 2.072908 | |
| Prob(F-statistic) | 0.00044 | |||
| Unweighted Statistics | ||||
| R-squared | 0.520907 | Mean dependent var | 0.005597 | |
| Sum squared resid | 0.086172 | Durbin-Watson stat | 2.072908 |
Tableau 13 : Modèle à effet fixe et aléatoire sur les banques locales (Auteur à partir de Eviews 9)
Les résultats d’estimation montrent que les coefficients associés à la rotation des actifs (drot) et au coefficient de fonds propres (dcfp) ne sont pas statistiquement significatifs car leurs p-value > 5% pour les deux modèles à effet individuel. La seule variable ayant un effet significatif sur la rentabilité financière des banques locales est la rentabilité des ventes (drcom) car p-value < au seuil de 1%.
Les coefficients de détermination ajusté semblent être faibles pour les modèles à effet fixe et aléatoire; soit respectivement de 39,66% et 46,10% ce qui traduit donc une faible qualité d’ajustement. Néanmoins, les deux modèles sont globalement significatifs car Prob (F-stat) < à 1%.
5.1.2. Tests post-estimations sur données de panel
⇒ Test de Hausman (1978)
Dans un modèle de régression sur les données de panel, le test de Hausman permet de vérifier si les coefficients des modèles à effets fixes et aléatoires sont statistiquement différents.
H0 : 𝛽𝐹 − 𝛽𝐴 = 0 il n’y a pas de différence entre le modèle à effet fixe et le modèle à effet aléatoire). Le modèle à effet aléatoire est approprié (Méthode de moindre carré généralisé)
H1 : 𝛽𝐹 − 𝛽𝐴 ≠ 0 Il existe une différence significative entre le modèle à effet fixe et le modèle aléatoire). Le modèle à effet fixe est approprié (Méthode de moindre carré ordinaire). Si la p-value est supérieure au seuil conventionnel de 5%, on accepte l’hypothèse nulle.
| Correlated Random Effects – Hausman Test | ||||
| Equation: Untitled | ||||
| Test cross-section random effects | ||||
| Test Summary | Chi-Sq. Statistic | Chi-Sq. d.f. | Prob. | |
| Cross-section random | 0.441063 | 3 | 0.9316 | |
| Cross-section random effects test comparisons: | ||||
| Variable | Fixed | Random | Var(Diff.) | Prob. |
| DRCOM | 0.077648 | 0.075442 | 0.000061 | 0.7778 |
| DROT | 1.024405 | 0.934179 | 0.105473 | 0.7812 |
| DCFP | 0.01624 | 0.014662 | 0.000026 | 0.7553 |
Tableau 14 : Test de Haussman sur le panel des banques locales
Les résultats de ce test montrent que le modèle à effet aléatoire est plus efficace car la p-value est supérieure au seuil conventionnel de 5%.
⇒ Test de Jarque-Bera (Normalité des résidus)
Le test de Jarque-Bera part de l’hypothèse nulle selon laquelle une série est distribuée normalement.
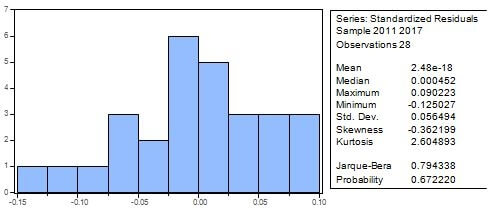
Etant donné que la probabilité du test est de 0,67 > 0,05, nous acceptons l’hypothèse nulle. Donc, les résidus sont distribués normalement.
⇒ Test d’autocorrélation des erreurs
Etant donné que la statistique de Durbin-Watson du modèle à effet aléatoire est de 2,0, nous pouvons accepter notre hypothèse nulle d’absence d’autocorrélation des erreurs.
5.2. Banques étrangères
5.2.1. Estimation du modèle à effet fixe et aléatoire
| Modèle à effet fixe | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| RCOM | 0.39828 | 0.055285 | 7.204088 | 0.0000 |
| ROT | 1.443346 | 0.940456 | 1.534729 | 0.1304 |
| DCFP | -0.017843 | 0.007878 | -2.265101 | 0.0273 |
| C | -0.160477 | 0.105346 | -1.523324 | 0.1332 |
| Effects Specification | ||||
| Cross-section fixed (dummy variables) | ||||
| R-squared | 0.713957 | Mean dependent var | -0.011385 | |
| Adjusted R-squared | 0.653737 | S.D. dependent var | 0.205207 | |
| S.E. of regression | 0.120752 | Akaike info criterion | -1.224165 | |
| Sum squared resid | 0.831124 | Schwarz criterion | -0.806588 | |
| Log likelihood | 55.84579 | Hannan-Quinn criter. | -1.058299 | |
| F-statistic | 11.8559 | Durbin-Watson stat | 2.063588 | |
| Prob(F-statistic) | 0.00000 |
| Modèle à effet aléatoire | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| RCOM | 0.419188 | 0.045895 | 9.133557 | 0.0000 |
| ROT | 0.216855 | 0.636867 | 0.340503 | 0.7346 |
| DCFP | -0.020578 | 0.007061 | -2.91417 | 0.0049 |
| C | -0.026181 | 0.073141 | -0.357953 | 0.7215 |
| Effects Specification | ||||
| S.D. | Rho | |||
| Cross-section random | 0.037108 | 0.0863 | ||
| Idiosyncratic random | 0.120752 | 0.9137 | ||
| Weighted Statistics | ||||
| R-squared | 0.616032 | Mean dependent var | -0.008834 | |
| Adjusted R-squared | 0.598579 | S.D. dependent var | 0.19336 | |
| S.E. of regression | 0.122509 | Sum squared resid | 0.990554 | |
| F-statistic | 35.29642 | Durbin-Watson stat | 1.590084 | |
| Prob(F-statistic) | 0.00000 | |||
| Unweighted Statistics | ||||
| R-squared | 0.628873 | Mean dependent var | -0.011385 | |
| Sum squared resid | 1.078345 | Durbin-Watson stat | 1.46063 |
Tableau 15 : Modèle à effet fixe et aléatoire sur les banques étrangères (Auteur à partir de Eviews 9)
5.2.2. Tests post-estimations sur données de panel
⇒ Test de Hausman (1978)
| Test Summary | Chi-Sq. Statistic | Chi-Sq. d.f. | Prob. | |
| Cross-section random | 4.933942 | 3 | 0.1767 | |
| Cross-section random effects test comparisons: | ||||
| Variable | Fixed | Random | Var(Diff.) | Prob. |
| RCOM | 0.39828 | 0.419188 | 0.00095 | 0.4976 |
| ROT | 1.443346 | 0.216855 | 0.478859 | 0.0763 |
| DCFP | -0.017843 | -0.020578 | 0.000012 | 0.4335 |
Les résultats de ce test montrent que le modèle à effet aléatoire est plus efficace car la p-value est supérieure au seuil conventionnel de 5%. Donc, l’estimateur MCG est non biaisé.
⇒ Test de Jarque-Bera (Normalité des résidus)
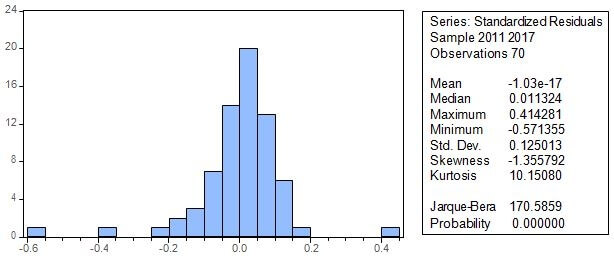
De visu, on remarque qu’il y a des observations aberrantes. La statistique de Jarque-Bera est très loin de zéro et sa probabilité correspondante est inférieure au seuil de 1%. Donc, nous rejetons l’hypothèse de normalité des résidus.
Il sied de noter que l’hypothèse de normalité des résidus est non indispensable pour le calcul des estimateurs mais nécessaire si on veut estimer le principe d’estimation du maximum de vraisemblance et pour procéder aux tests d’inférence. (Bosonga, 2017, p.86).
⇒ Test d’autocorrélation des erreurs
Etant donné que la statistique de Durbin-Watson du modèle à effet aléatoire est proche de 2, nous pouvons accepter notre hypothèse nulle d’absence d’autocorrélation des erreurs.
17 Vous trouverez en annexe 2, les estimations des paramètres de chaque banque ainsi que les résultats sur le test VIF (Variance Inflation Factor) de détection de multicolinéarité.
Le deuxième chapitre avait pour objectif de vérifier l’application du modèle de Dupont dans les banques commerciales afin d’identifier du point de vue statistique, la variable la plus significative pouvant expliquer la variabilité de la rentabilité financière des banques.
