Analyse économétrique
II. Approche méthodologique et spécification du modèle économétrique
1. Sources des données
Les données utilisées dans notre analyse empirique ont été collectées à partir des états financiers certifiés de quatorze banques commerciales en RDC. Nous nous sommes principalement servi des bilans et des comptes de profit et pertes pour ressortir et calculer les différents ratios se trouvant dans notre modèle.
Afin de pouvoir mieux identifier la variable la plus significative du modèle de Dupont, nous avons opté pour une représentation des données à double dimension : individuelle (i) avec 14 banques (10 banques locales et 4 banques étrangères) et temporelle (t) sur une période allant de 2010 à 2017.
2. Présentation et spécification du modèle de Dupont (1960)
› Référence à la théorie
« La réalisation des travaux économétriques doit nécessairement prendre comme point de départ une théorie économique, puisqu’elle suggère le type de relation à vérifier sur base des données réelles observées. » (Bosonga, 2017, p.10)
C’est ainsi que nous commençons par présenter l’équation de base du modèle de Dupont qui est la relation d’identité suivante :

RN = Résultat Net; PNB = Produit Net Bancaire; FP = Fonds propres.
| Code | Concepts | Description | Mesure | Type de variable | Signe attendu |
| ROE | Performance financière | Capacité à rémunérer les détenteurs des capitaux (Actionnaires) | Rentabilité financière | Endogène/ Quantitative | |
| RCOM | Profitabilité | Capacité à réaliser des profits élevés grâce à la maitrise des coûts (Efficience) | Taux de marge nette | Exogène/ Quantitative | + |
| ROT | Gestion efficace des actifs | Capacité à réaliser un chiffre d’affaires (PNB) élevé en fonction des actifs. | Coefficient de rotation des actifs | Exogène/ Quantitative | + |
| CFP | Niveau d’endettement | Capacité à améliorer la rentabilité suite à une augmentation du niveau d’endettement (Effet de levier). | Coefficient de fonds propres | Exogène/ Quantitative | + |
Tableau 1 : Présentation et prédiction des signes des variables (Auteur)
⇒ Spécification du modèle mathématique
Partant du modèle théorique présenté ci-dessus, la spécification mathématique se présente comme suit :

Nous modifions donc le modèle (3) :
𝑅𝑂𝐸 = 𝜶 + 𝜷𝟏 𝑅𝐶𝑂𝑀 + 𝜷𝟐 𝑅𝑂𝑇 + 𝜷𝟑 𝐶𝐹𝑃 (3)
#⇒ Spécification du modèle économétrique
Compte tenu des limites liées au caractère déterministe d’une relation mathématique, nous allons introduire le terme d’erreur (ε) pour transformer le modèle déterministe en modèle aléatoire.
Notre modèle (3) devient :
𝑅𝑂𝐸𝑖𝑡 = 𝜶𝟎𝒊 + 𝜷𝒊 𝑋𝑖𝑡 + 𝜀𝑖𝑡 (4)
𝑹𝑶𝑬𝒊𝒕 = Rentabilité financière (Return on Equity) observée pour la banque i à l’instant t;
𝜶𝟎𝒊 Est le terme constant;
𝑋𝑖𝑡 est le vecteur des variables exogènes : 𝑅𝐶𝑂𝑀 , 𝑅𝑂𝑇𝑖𝑡 et 𝐶𝐹𝑃𝑖𝑡
𝜷𝒊 est le vecteur des coefficients des variables 𝑅𝐶𝑂𝑀 , 𝑅𝑂𝑇𝑖𝑡 et 𝐶𝐹𝑃𝑖𝑡;
𝜺𝒊𝒕 Est le terme d’erreur, qui prend en comptes le reste des variables négligées dans le modèle.
III. Analyse économétrique de la rentabilité financière des banques commerciales en RDC (Modèle de Dupont)
Dans cette section, nous commencerons d’abord par vérifier la stationnarité des séries; ensuite, nous allons identifier la structure de nos panels; et enfin, nous allons procéder par les analyses uni- variées, bi-variées et multi-variées conformément à l’approche méthodologique retenue.
1. Test de stationnarité 8
Avant le traitement d’une série chronologique, il convient d’en étudier les caractéristiques stochastiques (Son espérance et sa variance). Si ces dernières se trouvent modifiées dans le temps, la série chronologique est considérée comme non stationnaire; dans le cas d’un processus stochastique invariant, la série temporelle est alors stationnaire. (Bourbonnais, 2015, p.239).
Lorsque nous sommes face à un panel, la différence essentielle réside dans le problème d’hétérogénéité du modèle qui ne se pose pas dans le contexte des séries temporelles. (Hurlin & Mignon, 2006,p.3).
Les tests les plus utilisés pour vérifier la stationnarité des séries en panel sont : Levin – Lin – Chu (2002), Im – Pesaran – Shin (2003), Harris – Tzavalis (1999), ADF (Augmented Dickey-Fuller).
Dans les tableaux ci-dessous, nous présentons les statistiques de chaque test ainsi que leurs p-value respectives sachant que tous les tests partent de l’hypothèse nulle selon laquelle les séries contiennent une racine unitaire (Non-Stationnaire).
Nous accepterons l’hypothèse nulle si les p- value d’au moins trois tests sont supérieurs au seuil conventionnel de 5%.
| Test de Racine Unitaire_Panel des banques locales | ||||||
| Variables | ADF | PP | Levin-Lin-Chu | Im-Pesaran-Shin | Harris-Tzavalis | Conclusion |
| Roe | 6,693 (0.570) | 6,693 (0.623) | -2,210 (0,013) | 0,174 (0,569) | 0,472 (0,122) | Non-Stationnaire |
| Rcom | 9,490 (0,303) | 13,087 (0,109) | -2,375 (0,008) | -0,309 (0,378) | 0,0243 (0,001) | Non-Stationnaire |
| Rot | 3,374 (0,908) | 3,640 (0,888) | -0,587 (0,278) | 0,941 (0,826) | 0,460 (0,108) | Non-Stationnaire |
| Cfp | 8,858 (0,354) | 6,264 (0,617) | -1,662 (0,048) | 0,212 (0,584) | 0,55 (0,242) | Non-Stationnaire |
Tableau 2 : Tests de Racine Unitaire sur le panel des banques locales (Auteur)
Les résultats des tests de stationnarité sur le panel des banques locales révèlent que toutes les variables contiennent une racine unitaire; c’est-à-dire que les caractéristiques des séries varient dans le temps.
| Test de Racine Unitaire_Panel des banques étrangères | ||||||
| Variables | ADF | PP | Levin-Lin-Chu | Im-Pesaran-Shin | Harris-Tzavalis | Conclusion |
| Roe | 38,00 (0,088) | 63,121 (0,000) | -6,295 (0,000) | -1,646 (0,049) | 0,073 (0,000) | Stationnaire |
| Rcom | 34,344 (0,024) | 93,373 (0,000) | 2,717 (0,996) | -1,161 (0,122) | 0,050 (0,000) | Stationnaire |
| Rot | 35,535 (0,017) | 47,898 (0,000) | -5,049 (0,000) | -1,564 (0,058) | 0,225 (0,000) | Stationnaire |
| Cfp | 18,552 (0,551) | 18,330 (0,566) | -1,511 (0,065) | 0,885 (0,812) | 0,779 (0,858) | Non-Stationnaire |
Tableau 3 : Tests de Racine Unitaire sur le panel des banques étrangères (Auteur)
Contrairement aux banques locales, juste la variable (cfp) est non-stationnaire.
2. Test d’homogénéité de Hsiao (1986)
En fonction de la spécification économétrique de notre modèle, nos données peuvent prendre quatre formes possibles (Bourbonnais R. , 2015) :
Homogénéité totale où les constantes 𝜶𝟎𝒊 et les coefficients 𝜷𝒊 sont les mêmes pour toutes les onze banques. (𝛼0𝑖 = 𝛼0 ) et (𝛽𝑖 = 𝛽 ). Si cette hypothèse est validée, la structure de panel est acceptée et nos paramètres seront estimés avec le MCO (Modèle Pooled) ou MCG en fonction de la structure de la matrice des variances et covariances des erreurs)
Hétérogénéité totale où les constantes 𝜶𝟎𝒊 et les coefficients 𝜷𝒊 sont différents pour toutes les valeurs des banques. . (𝛼0𝑖 ≠ 𝛼0 ) et (𝛽𝑖 ≠ 𝛽 ). Cela signifie que chaque banque évolue avec un comportement assez particulier. Donc, la structure de panel sera rejetée et le modèle sera estimé équation par équation (une équation par banque).
Hétérogénéité des coefficients des variables explicatives et homogénéité des termes constants; (𝛼0𝑖 = 𝛼0) et (𝛽𝑖 ≠ 𝛽). Ce cas est similaire au précédant; donc la structure de panel sera rejetée.
Hétérogénéité des termes constants et homogénéité des coefficients des variables explicatives (𝛼0𝑖 ≠ 𝛼0) et (𝛽𝑖 = 𝛽). Le panel aura la structure d’un modèle à effets individuels. Les études menées sur la rentabilité des banques par (Yao, 2005); (Molyneux & Thornton, 1992); (Abderazek, 2010); (Koli, 2013); (Uvoya, 2015) ont estimé les paramètres avec un modèle à effet individuel.
Nous allons vérifier la structure de nos panels en suivant la procédure séquentielle de Hsiao (1986). Trois tests seront effectués pour valider nos hypothèses nulles en utilisant la statistique de Fisher9 :
![]()
𝑺𝑪𝑹𝒄𝟏 est la somme des carrés des résidus du modèle contraint sous l’hypothèse nulle; estimé à partir de MCO;
SCR est la somme des carrés des résidus du modèle non contraint. Il s’agit de la somme des carrés des résidus des modèles estimés sur les t observations de chaque équation individuelle.
(𝒊 − 𝟏)(𝒌 + 𝟏) est le degré de liberté du numérateur; avec i nombre d’individus et k nombre des variables exogènes. On note ddln
[𝒊 × 𝒕 − (𝒌 + 𝟏)] est le degré de liberté du dénominateur; avec i nombre d’individus et k nombre des variables exogènes. On note ddld.
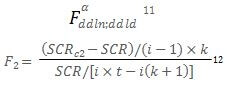
𝑺𝑪𝑹𝒄𝟐 est la somme des carrés des résidus du modèle contraint sous l’hypothèse nulle; estimé à partir du modèle à effets fixes individuels;
SCR est la somme des carrés des résidus du modèle non contraint.
(𝒊 − 𝟏) × 𝒌 est le degré de liberté du numérateur; avec i nombre d’individus et k nombre des variables exogènes. On note ddln
[𝒊 × 𝒕 − (𝒌 + 𝟏)] est le degré de liberté du dénominateur; avec i nombre d’individus et k nombre des variables exogènes. On note ddld.
Si la valeur de F2 > , on rejette l’hypothèse nulle du Test2 de Hsiao.
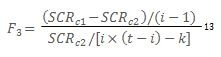
𝑺𝑪𝑹𝒄𝟐 est la somme des carrés des résidus du modèle contraint sous l’hypothèse nulle du Test 2;
𝑺𝑪𝑹𝒄𝟏 est la somme des carrés des résidus du modèle contraint sous l’hypothèse nulle du Test 1.
(𝒊 − 𝟏) est le degré de liberté du numérateur; avec i nombre d’individus. On note ddln
[𝒊 × (𝒕 − 𝒊) − 𝒌] est le degré de liberté du dénominateur; avec i nombre d’individus et k nombre des variables exogènes. On note ddld.
Si la valeur de F3 > 𝐹𝛼, on rejette l’hypothèse nulle du Test2 de Hsiao.
2.1. Tests d’homogénéité sur le Panel des banques locales
La condition sine qua non pour calculer les statistiques de Fisher est que les variables (K + 1) soient inferieures à la dimension temporelles (t). Pour notre étude, K=4+1 < t=8. Donc, nous pouvons calculer les statistiques de Fisher ainsi que leurs p-value respectives.14
| Test d’homogénéité | Statistique de Fisher & p-value | Conclusion | Modèle à utiliser | |
| Test 1 | F1 = 6,19048 | H0 rejetée; Donc, les constantes sont différentes | Passer au Test 2 | |
| H0 : (𝛼0𝑖 = 𝛼0 ) et | 𝑭𝟎.𝟎𝟓 = 2,42 𝟏𝟐;𝟏𝟔 | |||
| (𝛽𝑖 = 𝛽) | ∀𝑖 | p-value = 0,00053373 | ||
| Test 2 | F2 = 7,7387273 | Ho rejetée ; | Estimation équation par équation | |
| H0 : (𝛽𝑖 = 𝛽) | ∀𝑖 | 𝑭𝟎.𝟎𝟓 = 2,54 𝟗;𝟏𝟔 | Hétérogénéité totale | |
| p-value = 0,00022972 | ||||
| Test 3 H0 : (𝛼0𝑖 = 𝛼0) ∀𝑖 |
Tableau 4 : Test d’homogénéité sur le panel des banques locales (Auteur)
Le test 1 part de l’hypothèse selon laquelle le panel a des coefficients et des constantes homogènes pour toutes les banques i; étant donné que F1 > 𝐹0.05 et que la p-value (0,00053373) associée à la statistique de Fisher du Test1 est inférieure au seuil conventionnel de 5%, nous rejetons l’hypothèse nulle d’homogénéité des constantes.
Ce qui nous pousse à vérifier si au moins les coefficients sont homogènes afin d’avoir un modèle à effet individuel; au test2, nous rejetons une fois de plus notre hypothèse nulle car F2 > 𝐹0.05 et p-value (0,00022972) < 5%.
Donc, sur base de ces résultats, nous pouvons conclure que notre base de données a une structure de panel totalement Hétérogène. Il faut donc, estimer les paramètres équation par équation pour chaque banque. (Bourbonnais R. , 2015)
2.2. Tests d’homogénéité sur le Panel des banques étrangères
Vérifions à présent si on peut avoir une structure de panel homogène au niveau des banques panafricaines. En respectant la condition que K+1 > t, les statiques de Fisher et leurs p-value se présentent comme suit :
| Test d’homogénéité | Statistique de Fisher & p-value | Conclusion | Modèle à utiliser |
| Test 1 H0 : (𝛼0𝑖 = 𝛼0 ) et (𝛽𝑖 = 𝛽) ∀𝑖 | F1 = 5.711917679284085 p-value = 0.0000025 | H0 rejetée; Donc, les constantes sont différentes | Passer au Test 2 |
| Test 2 H0 : (𝛽𝑖 = 𝛽) ∀𝑖 | F2 = 5.64232417174344 p-value = 0.0000056 | Ho rejetée; Hétérogénéité totale | Estimation équation par équation |
| Test 3 |
Tableau 5 : Test d’homogénéité sur le panel des banques étrangères (Auteur)
Les p-values des statistiques de Fisher 1 et Fisher 2 sont respectivement de 0.0000025 et 0.0000056 < au seuil conventionnel de 5%. Toutes les valeurs de F-calculé sont également supérieures aux F-tabulaire. Nous rejetons les hypothèses nulles de deux premiers tests. Donc, nous confirmons la présence d’hétérogénéité totale des banques étrangères.
3. Analyse uni variée
Il sera question sur ce point de procéder à une analyse descriptive de nos variables et de tester certaines hypothèses sur la distribution des données : Test de normalité
3.1. Descriptions des variables 15
⇒ Panel des banques locales
| Variable | Obs | Mean | Std. Dev. | Min | Max |
| roe | 32 | .0993837 | .0887715 | -.0740391 | .2421724 |
| rcom | 32 | .0477525 | .3414426 | -1.365688 | .438101 |
| rot | 32 | .1031775 | .0397379 | .0350293 | .2100217 |
| cfp | 32 | 7.849213 | 3.164507 | 1.262065 | 12.13798 |
Tableau 6 : Description des variables des banques locales (Auteur)
La ROE moyenne des banques commerciales locales de 2010 à 2017 est de 9,9% avec une déviation standard de 8,87%. La ROE la moins élevée est de -7,4% et a été réalisée par SOFIBANQUE en 2011. La ROE la plus élevée est de 24,21% toujours réalisée par SOFIBANQUE en 2016.
Il faut noter que la banque a débuté ses activités le 1er janvier 2010 avec une seule agence à Kinshasa, ce qui justifie donc le fait que ses premières années soient caractérisées par des ROE négatives dues aux résultats déficitaires. Depuis 2013, SOFIBANQUE a élargi son réseau et dispose de plusieurs agences à Kinshasa, Matadi, Lubumbashi, Kolwezi, Mbuji-Mayi, et Goma.
On remarque alors une amélioration du PNB. Ce qui fait que SOFIBANQUE soit la banque la plus rentable de 2013 à 2017. (Voir figure 3)
Le taux de marge (rcom) moyen est très faible et s’élève à 4,77%; le minimum est de -136,56% réalisé par SOFIBANQUE en 2010 et le maximum, de 43,81% réalisé encore une fois par SOFIBANQUE en 2016. Ces chiffres s’expliquent encore une fois par le fait que la banque ait développé son réseau d’agences en RDC.
Le coefficient de rotation des actifs (rot) moyen est de 0,1; le minimum est de 0,03 réalisé par SOFIBANQUE en 2010 et le maximum est de 0,21 réalisé par SOFIBANQUE en 2017. Les banques semblent avoir des coefficients de rotation des actifs faibles à cause de la nature de leurs activités qui leur oblige à recouvrer des créances à long terme.
Le coefficient des fonds propres (cfp) moyen est de 7,84 avec un écart-type de 3,16; le minimum s’élève à 1,26 réalisé par SOFIBANQUE en 2011 et le maximum est de 12.14 réalisé par la BCDC en 2015. La BCDC est la banque ayant atteint le niveau d’endettement le plus élevé.
De part ces statistiques, SOFIBANQUE semble avoir des rentabilités très élevées par rapport aux autres banques locales.
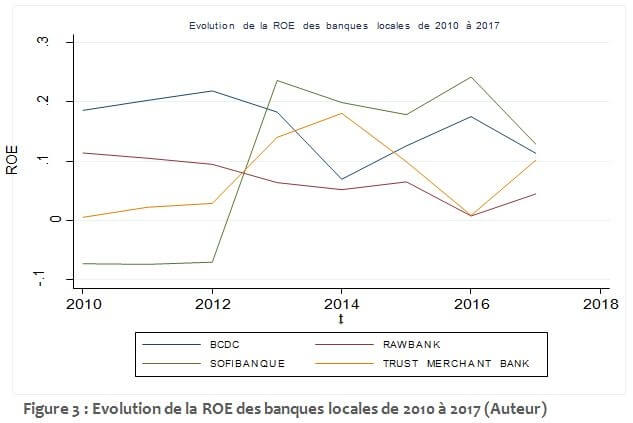
Figure 3 : Evolution de la ROE des banques locales de 2010 à 2017 (Auteur)
En observant le graphique ci-dessus, on constate que les courbes de ROE des banques ont des évolutions assez différentes. Une banque semble avoir des rentabilités plus ou moins stables; c’est le cas de RAWBANK; tandis que d’autres, semblent être plus volatiles.
Les actionnaires d’une banque telle que TRUST MERCHANT BANK ou SOFIBANQUE peuvent anticiper des grandes fluctuations dans la performance financière de leur entreprise.
On remarque également que les banques locales ont eu à réaliser des rentabilités financières positives de 2010 à 2017. SOFIBANQUE était moins rentable de 2010 à 2012 mais la plus rentable de 2013 à 2017.
⇒ Panel des banques étrangères
| Variable | Obs | Mean | Std. Dev. | Min | Max |
| roe | 80 | -.0210539 | .2141509 | -.9898075 | .2524416 |
| rcom | 80 | -.2265967 | 1.419023 | -10.39744 | .7836087 |
| rot | 80 | .1058075 | .033462 | .0031055 | .175278 |
| cfp | 80 | 6.965758 | 4.240309 | 1.37478 | 24.69865 |
Tableau 7 : Description des variables des banques étrangères (Auteur)
La ROE moyenne des banques étrangères est de -2% avec un écart-type de 21,4%. La rentabilité la plus faible, soit de -98,98% a été réalisée par ACCES BANK en 2013 à cause d’un résultat net déficitaire d’environ -5 255 500 USD (1$ = 925,5 CDF) et la plus élevée est de 25,24% réalisée par BGFI en 2015 car depuis 2013, la banque a eu à développer un réseau de 7 agences en RDC ce qui a fait grimper rapidement son PNB et a amélioré la rentabilité.
Le taux de marge nette (rcom) moyen est de -22,66% avec une déviation de 141,9%. Le minimum s’élève à -1039,7% réalisé par BGFI en 2010 causé par une perte nette d’environ 1 397 472 USD (1$=910) mais également à cause d’un faible niveau de PNB car la banque venait à peine de commencer ses activités en RDC et le maximum est de 78,36% réalisé par BGFI en 2012.
Le coefficient de rotation des actifs (rot) moyen s’élève à 0,105 qui est légèrement plus faible que de celui des banques les plus locales. Le coefficient minimum est de 0,0031 réalisé par BGFI en 2010 et le maximum est de 0,175 réalisé par ACCESS BANK en 2010.
Le coefficient des fonds propres (cdf) moyen est de 6,96; il est légèrement inférieur des banques locales (7,85). La banque étrangère ayant le niveau d’endettement le plus faible est BYBLOS BANK en 2011 avec un coefficient des fonds propres de 1,37.
Le coefficient maximum est de 24,70 réalisé par FBN BANK en 2017 et il sied de noter que la banque a clôturé son exercice comptable avec une perte nette d’environ -5 254 855 $ et une ROE de -36%.
Il semble donc que la FBN ne profite pas suffisamment des effets de l’endettement.
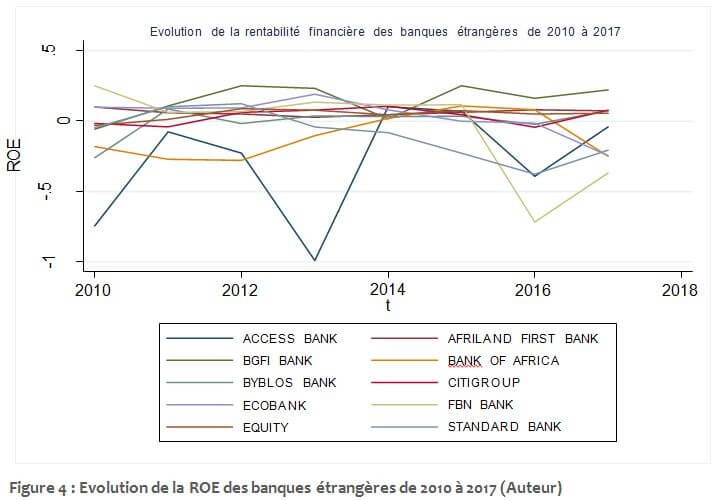
Figure 4 : Evolution de la ROE des banques étrangères de 2010 à 2017 (Auteur)
De visu, on peut constater à partir du graphique ci-dessus que les banques étrangères ont des courbes de ROE évoluant à la zone négative ou proche de zéro. Elles sont donc moins rentables que les banques locales. Une seule banque semble se distinguer des autres avec des rentabilités financières plus élevées, il s’agit de BGFI.
FBN BANK avait une courbe de ROE plus ou moins stable de 2010 à 2015; mais on remarque des grandes fluctuations en 2016 et 2017.
⇒ Courbes de ROE des banques commerciales congolaises de 2010 à 2017
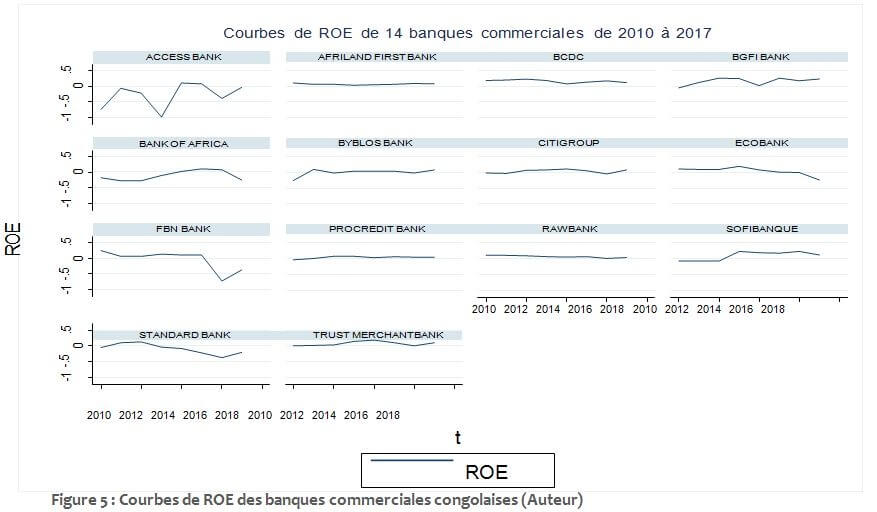
Figure 5 : Courbes de ROE des banques commerciales congolaises (Auteur)
En observant les courbes de taux de rentabilité financière des banques commerciales congolaises, nous remarquons que les banques locales semblent être plus rentables et moins volatiles que les banques étrangères.
Nous discuterons des facteurs pouvant expliquer les différences des rentabilités des banques commerciales congolaises lors de l’analyse multi variée. Néanmoins, les analyses descriptives peuvent se résumer comme suit :
| Catégories | ||||||
| Banques locales | 3.9% | 5% | 0.10318 | 1.2% | 7.84921 | 13% |
| Banques étrangères | -1.8% | -23% | 0.10581 | -0.3% | 6.96576 | 14% |
| Moyenne du secteur | -5% | -6% | 0.1020 | -0.61% | 4.93832 | 9% |
Tableau 8 : Résumé des analyses descriptives des banques commerciales (Auteur)
En observant le tableau 8, on remarque clairement qu’en moyenne, les banques locales ont une rentabilité financière plus élevée que les banques étrangères.
Les banques locales semblent avoir des ROE élevées puisque leurs taux de marge nette (RCOM) sont également élevés. Le même constat peut se faire au niveau des autres banques.
Par ailleurs, les coefficients de rotation des actifs (rot) ainsi que les coefficients de fonds propres (cfp) semblent être les mêmes pour les deux catégories des banques.
A partir de ces statistiques, nous pouvons vérifier certaines normes sectorielles si elles existent ou cas contraire, procéder par un benchmark pour avoir des modèles de référence.
En décomposant le ratio de taux de marge, on remarque que son niveau est conditionné par le résultat net obtenu à la fin de l’exercice comptable.
Donc, il peut mesurer la capacité d’une banque à pouvoir maitriser l’ensemble des charges tel que dit au chapitre 1; et plus particulièrement, les charges d’exploitation car elle peut certes réaliser un produit net bancaire (PNB) très élevé; mais si elle n’est pas efficiente, cette création de valeur sera étouffée par des charges fixes ou variables et cela peut se manifester à travers un coefficient d’exploitation (CIR) très élevé.
Par conséquent, nous pouvons établir un lien entre le ratio de taux de marge nette et le coefficient d’exploitation des banques. Un taux de marge nette élevée se traduira donc par un coefficient d’exploitation faible.
Selon les normes sectorielles, le coefficient d’exploitation doit être compris entre 60 et 70%.
Concernant le coefficient de rotation des actifs, nous pouvons nous servir de la moyenne du secteur comme modèle de référence, soit de 0,1. Si une banque a une rotation des actifs < 0,1, cela signifie qu’elle a une gestion inefficace des actifs et risque de réaliser une rentabilité financière faible.
Nous avons calculé l’inverse de la moyenne du coefficient de fonds propres juste pour vérifier si globalement les banques commerciales en RDC respectent la norme relative au ratio de levier financier. Les résultats des analyses descriptives nous prouvent donc que globalement, les banques respectent la norme car le ratio moyen est > à 5%.
3.2. Test de normalité des variables
Avant de passer à l’analyse bi variée, il est important de vérifier si toutes nos variables sont distribuées normalement. Etant donné que nos panels sont tous, hétérogènes, il sera préférable de vérifier pour chaque banque.
Pour des petits échantillons, généralement inférieurs à 30 observations, il est recommandé d’utiliser le test de Shapiro-Wilk (Bosonga, 2017).
Pour le cas de notre étude, chaque banque est observée pendant 8 exercices comptables. Donc, nous allons utiliser le Test de Shapiro et Wilk (1965) avec comme hypothèse nulle : Les distributions de l’échantillon suivent la loi normale. La statistique de test (W) est calculée par la formule :
[∑𝑛/2 𝑎𝑗 𝑑𝑗]2
𝑊 =
∑𝑛
(𝑥𝑖 − 𝑥̅)2
𝑖=1
aj = Les coefficients fournis par la table de coefficient de Shapiro dj = x (n-i+1) – xi
xi = série ordonnée selon l’ordre croissant
x (n-i+1) = série ordonnée selon l’ordre décroissant
𝑥̅ = moyenne de la série.
16Au niveau des banques locales, les résultats des tests de normalité nous renseignent que :
- ⇒ BCDC et TMB ont toutes, des variables qui sont distribuées normalement;
- ⇒ Toutes les variables de RAWBANK suivent la loi normale sauf la variable cfp (Coefficient de fonds propres);
- ⇒ Pour SOFIBANQUE, les variables rot (Coefficient de rotation des actifs) et cfp (Coefficient de fonds propres) suivent une loi normale; mais roe (Rentabilité financière) et rcom (Taux de marge) sont anormalement distribuées;
Les tests de Shapiro et Wilk (1965) nous renseigne qu’au niveau des banques étrangères :
- ⇒ Toutes les variables de AFRILAND DFIRST BANK suivent une loi gaussienne
- ⇒ PROCREDIT et BGFI, ont des variables gaussiennes sauf rcom.
- ⇒ Toutes les variables de FBN ne sont pas gaussiennes;
- ⇒ Les variables de ACCESS BANK et ECOBANK suivent une loi normale sauf la variable cfp;
- ⇒ Toutes les variables de BOA sont distribuées normalement sauf rcom;
- ⇒ Toutes les variables de STANDARD BANK et CITIGROUP suivent une loi gaussienne;
- ⇒ Pour BYBLOS, la roe et rcom ne sont pas distribuées normalement; juste les variables rot et cfp qui sont normales.
4. Analyse bi variée
En fonction de la description de chaque variable, nous allons à présent vérifier l’existence, le sens et l’intensité d’un lien entre la variable endogène (roe) et chaque variable exogène (rcom, rot et cfp).
Etant donné que toutes nos variables sont quantitatives, nous allons utiliser principalement deux tests en fonction de la nature de la distribution : Test de corrélation de Bravais-Pearson (1896) pour les variables distribuées normalement et le Test de corrélation des rangs de Spearman (1904) pour les distributions non gaussiennes.
Les résultats de cette analyse bi variée, peuvent nous permettre d’effleurer la vérification de nos hypothèses de recherche.
4.1. Test de corrélation des variables
Les coefficients de corrélation simple sont calculés et présentés pour chaque banque sur les tableaux ci-dessous en fonction du type de la distribution de la variable.
Nous présentons également les coefficients de corrélation entre les variables explicatives afin d’observer s’il pourrait avoir un risque de multicolinéarité.
La significativité d’un coefficient est au seuil conventionnel de 5%; les coefficients de corrélation significatifs sont représentés par *. S’il est écrit en rouge suivi d’un * cela représente un risque de multicolinéarité entre les variables exogènes.
⇒ Coefficients de corrélation pour les variables des banques locales
| Corrélation (y et xi) | |||||||
| Banques | ρ(roe,rcom) | Test | ρ(roe,rot) | Test | ρ(roe,cfp) | Test | |
| 1 | BCDC | 0.8699* | Pearson | 0.4803 | Pearson | -0.2436 | Pearson |
| 2 | RAWBANK | 0.9967* | Pearson | 0.5199 | Pearson | -0.6667 | Spearman |
| 3 | SOFIBANQUE | 0.9286* | Spearman | 0.2143 | Spearman | 0.8333* | Spearman |
| 4 | TMB | 0.9873* | Pearson | 0.9621* | Pearson | 0.6056 | Pearson |
Tableau 9 : Coefficients de corrélation pour les variables des banques locales (Auteur)
La variable rcom (Taux de marge nette) est fortement, positivement et significativement correlée avec la rentabilité financière pour toutes les banques locales.
Nous remarquons l’existence des correlations positives entre le coefficient de rotation des actifs et la rentabilité financiere de chaque banque; mais cette relation n’est significative que pour TRUST MERCHAN BANK.
En ce qui concerne le coefficient de fonds propres, il est negativement correlé avec la rentabilité financiere de BCDC et RAWBANK mais non significatif; positivement, fortement et significativement correlé avec la rentabilité financière de SOFIBANQUE.
Nous avons toutefois identifié des fortes correlations significatives entre les variables explicatives :
| Corrélation des variables exogènes | ||||
| Banques | ρ (rcom,cfp) | ρ (rcom,rot) | ρ (rot,cfp) | |
| 1 | BCDC | -0.5751 | 0.0607 | 0.1467 |
| 2 | RAWBANK | -0.6667 | 0.5113 | -0.7619* |
| 3 | SOFIBANQUE | 0.7381* | 0.0952 | 0.5714 |
| 4 | TMB | 0.5691 | 0.9450* | 0.61 |
Tableau 10 : Coefficients de corrélation pour les variables exogènes des banques locales (Auteur)
Une relation négative et significative entre le coefficient de rotation des actifs et le coefficient de fonds propres auprès de RAWBANK; une corrélation positive ente le taux de marge et le coefficient de fonds propres auprès de SOFIBANQUE et une forte corrélation positive et significative entre le taux de marge nette et la rotation des actifs auprès de TMB.
⇒ Coefficients de corrélation pour les variables des banques étrangères
| Corrélation (y et xi) | |||||||
| Banques | ρ(roe,rcom) | Test | ρ(roe,rot) | Test | ρ(roe,cfp) | Test | |
| 1 | ACCESS | 0.9396* | Pearson | 0.0071 | Pearson | -0.5952 | Spearman |
| 2 | AFRILAND | 0.9077* | Pearson | -0.3582 | Pearson | 0.7907* | Pearson |
| 3 | BGFI | 0.7381* | Spearman | 0.4669 | Pearson | 0.1855 | Pearson |
| 4 | BOA | 0.8333* | Spearman | 0.5876 | Pearson | 0.3189 | Pearson |
| 5 | ECOBANK | 0.9895* | Pearson | 0.6987* | Pearson | -0.5476 | Spearman |
| 6 | FBN | 0.9524* | Spearman | 0.4048 | Spearman | -0.3571 | Spearman |
| 7 | PROCREDIT | 0.7857* | Spearman | 0.3955 | Pearson | 0.2775 | Pearson |
| 8 | BYBLOS | 1* | Spearman | 0.4524 | Spearman | -0.1429 | Spearman |
| 9 | CITIGROUP | 0.9297* | Pearson | 0.5102 | Pearson | 0.704* | Pearson |
| 10 | STANDARD | 0.9621* | Pearson | 0.6688 | Pearson | -0.2381 | Pearson |
Tableau 11 : Coefficients de corrélation pour les variables des banques étrangères (Auteur)
La variable rcom (Taux de marge nette) est fortement, positivement et significativement correlée avec la rentabilité financière pour toutes les banques étrangères (Panafricaines et internationales).
Le coefficient de corrélation du coefficient de rotation des actifs n’est pas significatif pour toutes les banques étrangères sauf pour ECOBANK;
Le coefficient de fonds propres est posivement et significativement lié qu’à la rentabilité financière de AFRILAND FIRST BANK et CITIGROUP. Les autres coefficients de correlation ne sont pas statistiquement significatifs.
Les coefficients de corrélation des variables explicatives des banques étrangères se presentent comme suit :
| Corrélation des variables exogènes | ||||
| Banques | ρ (rcom,cfp) | ρ (rcom,rot) | ρ (rot,cfp) | |
| 1 | ACCESS | -0.5 | -0.029 | -0.7857* |
| 2 | AFRILAND | 0.5147 | -0.5051 | -0.3749 |
| 3 | BGFI | -0.19 | -0.1429 | 0.7888* |
| 4 | BOA | 0.5952 | 0.9524* | 0.7 |
| 5 | ECOBANK | -0.5952 | 0.6492 | -0.5476 |
| 6 | FBN | -0.5238 | 0.5476 | -0.8333* |
| 7 | PROCREDIT | -0.4048 | 0.1905 | 0.2775 |
| 8 | BYBLOS | -0.1429 | 0.4524 | 0.0238 |
| 9 | CITIGROUP | 0.8017* | 0.674 | 0.4105 |
| 10 | STANDARD | -0.0182 | 0.6791 | -0.4397 |
Tableau 12 : Coefficients de corrélation pour les variables exogènes des banques étrangères (Auteur)
Le risque de multicolinearité peut se presenter entre les variables : Rotation des actifs et coefficient de fonds propres de ACCESS BANK et BGFI; Taux de marge nette et rotation des actifs de BOA; et rotation des actif et coefficient de fonds propres de FBN BANK. Taux de marge nette et coefficients de fonds propres de CITIGROUP.
Sur base des résultats des analyses bi variées, nous avons donc remarqué que le taux de marge nette (Rentabilité commerciale ou rentabilité des ventes) est la seule variable correlée positivement et significativement avec la rentabilité financière pour toutes les quatorse banques commerciales sous étude.
Nous pouvons déjà vérifier notre toute première hypothèse selon laquelle il existerait une relation positive entre le taux de marge et la rentabilité financière des banques commerciales.
Le point suivant examinera de manière exhaustive les variables afin d’identifier des relations de causalité.
_________________________________
8 Vous trouverez en annexe 3, les détails sur le test de racine unitaire ainsi que le processus de stationnaristion des séries.
9 Tous les calculs seront effectués automatiquement à l’aide des programmes complémentaires des logiciels Eviews 9 et Stat 13.
10 Il s’agit du F calculé pour le test 1 de Hsiao ARISTIDE MAKALAKA
11 Il s’agit de la valeur lue dans la table de Fisher aux degrés de liberté ddln=V1 et ddld=V2 avec un seuil de significativité de 5%. Si F1 > 𝐹𝛼 on rejette l’hypothèse nulle.
12 Si au Test 1, l’hypothèse nulle a été acceptée, il ne sera plus important de calculer encore F2 puisque la structure de Panel sera déjà connue (Homogénéité totale).
15 Toutes les variables sont exprimées en valeur absolue
13 Si au Test 2, l’hypothèse nulle a été rejetée, il ne sera plus important de calculer encore F3 puisque la structure de Panel sera déjà connue (Hétérogénéité totale).
14 Les valeurs des F et p-values ont été calculées à partir des logiciels Stata 13 et Eviews 9.
16 Vous trouverez en annexe 4, les détails sur les statistiques de Shapiro et Wilk ainsi que leurs p-value respectives.