Les stratégies d’implémentation machine révèlent des solutions innovantes pour des essais de fatigue en flexion plane. En intégrant des modèles théoriques et des simulations avancées, cette recherche promet de transformer les pratiques d’essai, avec des implications significatives pour l’industrie.
Chapitre 3 : Le dimensionnement
Introduction
Le mot conception ne représente pas juste la géométrie, mais également le calcul RDM pour le dimensionnement
Le dimensionnement consiste à calculer les dimensions en fonction des sollicitations en choisissant un critère pour le calcul.
Dans ce chapitre, on va faire des modélisations pour assimiler les pièces de notre machine à un modèle théorique convenable et aussi utiliser le logiciel SOLIDWORKS pour différentes simulations et interprétant les résultats trouvés.
Dimensionnement de l’éprouvette
Pour estimer à peu près les dimensions de la machine on va commencer par dimensionner l’éprouvette. Donc il est nécessaire de trouver une relation entre la forme, la flèche et la contrainte de flexion maximale en utilisant les théories de RDM.
Distribution de contrainte
La théorie des poutres est une application de la théorie de l’élasticité isotrope. Pour mener les calculs de résistance des matériaux, on adopte les hypothèses fondamentales de la RDM.
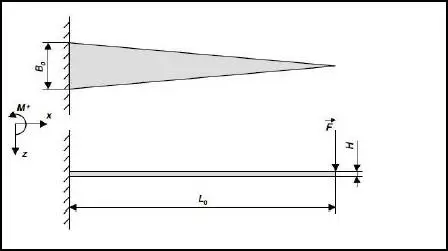
Figure 3.1 Représentation de la poutre
On assimile l’éprouvette à une poutre en porte-à faux schématisée dans la figure 2.1, encastrée d’un côté, libre à l’autre. Pour une charge concentrée, appliquée à l’extrémité libre, le moment fléchissant est proportionnel à l’abscisse x, or pour un bon déroulement de l’essai on est contraint d’avoir une contrainte constante tout au long de la longueur utile.
C’est ce qui justifie l’utilisation d’éprouvettes présentant une section d’égale résistance, on s’appuie sur les calculs de [13].
Explicitons maintenant le lien existant entre la contrainte 𝜎 et le moment fléchissant 𝑀𝑓. Dans une section droite, L. Navier a démontré que toute fibre longitudinale située à une distance y de l’axe neutre est le siège d’une contrainte donnée par la formule suivante :
𝜎 = 𝑀𝑓.𝑦
𝐼
…2.1.1.
Tel que représente 𝜎 la contrainte, 𝑀𝑓 le moment fléchissant, I le moment quadratique calculé en fonction de la forme de la section droite.
Si de plus la poutre est symétrique par rapport à son plan neutre 𝑦 = 𝐻 ,
2
l’équation devient :
𝜎𝑚𝑎𝑥
= 𝑀𝑓.𝐻
2𝐼
…2.1.2.
Où H représente l’épaisseur de l’éprouvette.
Le moment quadratique d’une section rectangulaire s’énonce comme suit
𝐼 = 𝐵𝐻3
12
…2.1.3.
Où B représente la largeur de l’éprouvette.
Pour une éprouvette qui présente un profil d’égale résistance, la largeur et de ce fait le moment quadratique dépend de l’abscisse. D’où :
𝐵(𝑥) = 𝐵0 (𝐿
− 𝑥) …2.1.4.
𝐿0 0
Où 𝐿0 représente longueur totale et 𝐵0 la largeur de la base. En substituant l’équation (2.1.4) dans l’équation (2.1.3), on obtient :
𝐵0(𝐿0−𝑥)𝐻3
𝐼(𝑥) =
12𝐿0
…2.1.5.
Pour une poutre montée en porte-à-faux, si l’effort est appliqué en un point à l’extrémité, le moment de flexion varie linéairement le long de l’éprouvette selon la formule suivante :
𝑀 = −𝐹(𝐿0 − 𝑥) …2.1.6.
Tel que F représente l’effort transversal s’exerçant dans le plan appliqué sur l’éprouvette à 𝑥 = 𝐿0 . En substituant l’équation (2.1.5) et (2.1.6) dans l’équation (2.1.2), on obtient :
𝜎𝑚𝑎𝑥
= − 6𝐹𝐿0
𝐵0𝐻2
…2.1.7.
La contrainte maximale est indépendante de la position de et uniforme tout au long de l’éprouvette. Elle présente bien un profil d’égale résistance.
La relation entre la flèche et contrainte
L’équation différentielle de la ligne élastique est donnée par :
𝜕2𝑦 = − 𝑀𝑓
…2.2.1.
𝜕𝑥2
𝐸𝐼
𝑦(𝑥) = 6𝐹𝐿0 𝑥2 …2.2.2.
𝐸𝐵0𝐻3
Si 𝑥 = 𝐿0 la déformation est maximale et 𝑧 prend donc la valeur maximale 𝑧0
appelée flèche.
𝐹 = 𝑍0𝐸𝐵0𝐻3
6𝐿3
0
…2.2.3.
𝜎𝑚𝑎𝑥
= − 𝑍0𝐸𝐻
0
𝐿2
…2.2.4.
Application numérique :
Les dimensions de l’éprouvette :
𝐿0 = 103 𝑚𝑚 𝐻 = 2 𝑚𝑚 𝐵0 = 50 𝑚𝑚
En choisissant une flèche 𝑍0 = 5 𝑚𝑚 et acier comme matériau on trouve :
𝐹 = 64.055 𝑁 et 𝜎𝑚𝑎𝑥 = 197.94 𝑀𝑝𝑎
On fait une simulation statique sur l’éprouvette et on trouve :
| Table III.1 | |
|---|---|
| Parameter/Criteria | Description/Value |
| Contrainte maximale | 5.5 ∗ 107 𝑃𝑎 |
| Déplacement maximal | 2 mm |
On remarque que le milieu de l’éprouvette a la même couleur ce qui il fait que dans cette partie l’éprouvette est subit à la même contrainte maximale environ de 𝜎𝑚𝑎𝑥 = 5.5 ∗ 107 𝑃𝑎 ce qui est inférieure à la limite
élastique 𝜎𝑒 = 1.75 ∗ 108 𝑃𝑎.On a aussi un déplacement maximale de 2 mm à l’extrémité libre ,il y a un déviance par rapport à la théorie des poutres.
Dimensionnement des plaques
Plaque de fixation
La longueur et la hauteur de la plaque sont imposées par le positionnement des éprouvettes par contre l’épaisseur est prise égale à 15mm.On va tester sa rigidité avec cette valeur.
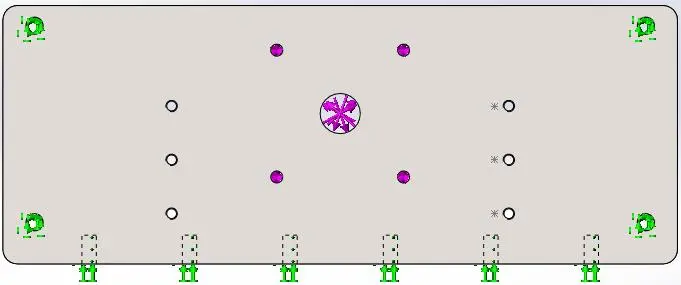
Figure 3.5 Sollicitation de la plaque de fixation
Cette plaque est fixé sur la base et avec les tiges (flèches verts) par des vises et supporte le moteur (les flèches violet), son poids est estimer de 40 𝑁.
On simule ces conditions limites et on trouve une contrainte et déplacement maximale de :
𝜎𝑚𝑎𝑥 = 1.8 ∗ 105 𝑃𝑎 𝑦𝑚𝑎𝑥 = 3.86 ∗ 10−6 𝑚𝑚
On est toujours dans la zone élastique et donc la rigidité est très satisfaisante.
Plaque de guidage
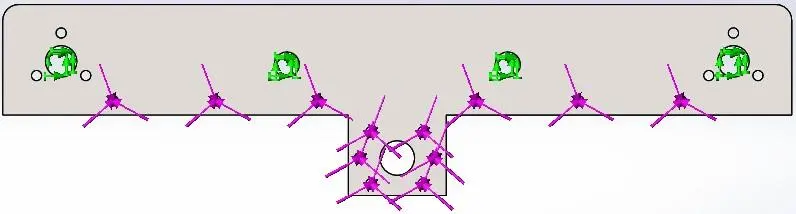
De même pour la plaque de guidage ces dimensions sont imposés par les éprouvettes (concernant la longueur et largeur) et pour l’épaisseur on a pris 10 mm et on va la vérifier.
Figure 3.6 Sollicitation de la plaque de guidage
On a fixé la plaque sur les 2 extrémités (liaison avec les tiges de guidage) et fixé au milieu (liaison avec l’entretoise) ,en évaluant l’effort appliqué sur elle (le poids des calles et la noix) par 100 𝑁 .
La simulation nous donne :
𝜎𝑚𝑎𝑥 = 4.6 ∗ 103 𝑃𝑎 𝑦𝑚𝑎𝑥 = 1.77 ∗ 10−7𝑚𝑚
D’après ces résultats on dit que la plaque est considérée indéformables.
Dimensionnement des tiges

Les tiges supportent les 2 plaques de guidages. Au début lorsque la machine est en arrêt les tiges sont soumises à la flexion.
Figure 3.7 Sollicitation de la tige de guidage
On a estimé le poids des plaques et les coussinets plus les bagues environ de 3.2 Kg. Pour une seul tige l’effort est de 16 N. on a trouvé
𝜎𝑚𝑎𝑥 = 2.49 ∗ 103 𝑃𝑎 et 𝑦𝑚𝑎𝑥 = 3.29 ∗ 10−8 𝑚𝑚. La tige en statique est considérée indéformable.
Lorsque la machine est en marche les tiges seront sollicitées à cause de leurs contacts avec les coussinets et le poids de la masse mobile.
En évaluant la force de frottement entre les tiges et la masse mobile :
𝑓 = 𝜇𝑚𝑔
𝑓, 𝜇 :la force et le coefficient de frottement de la tige avec coussinet.
𝑚 :la masse du bague et coussinet et partie de la plaque de guidage. La contrainte tangentielle due au frottement des coussinets sur la tige :
𝑓 0.0808
𝑟 = 𝑆 = 𝜋 ∗ 16 ∗ 30 ∗ 10−6 = 53.5822 𝑃𝑎
D’après les résultats précédents et celle-ci on peut dire que les tiges sont convenables pour le fonctionnement de la machine.
Questions Fréquemment Posées
Comment dimensionner une éprouvette pour des essais de fatigue en flexion?
Le dimensionnement consiste à calculer les dimensions en fonction des sollicitations en choisissant un critère pour le calcul, et nécessite de trouver une relation entre la forme, la flèche et la contrainte de flexion maximale.
Quelle est la formule pour calculer la contrainte maximale dans une éprouvette?
La contrainte maximale est donnée par la formule 𝜎𝑚𝑎𝑥 = 𝑀𝑓.𝐻 / (2𝐼), où 𝑀𝑓 est le moment fléchissant, H l’épaisseur de l’éprouvette, et I le moment quadratique.
Quels logiciels sont utilisés pour la modélisation et les simulations dans la conception de la machine?
Le logiciel SOLIDWORKS est utilisé pour différentes simulations et pour interpréter les résultats trouvés lors de la modélisation des pièces de la machine.
