L’optique sans fil OSF dans les réseaux GSM
4.3. L’optique sans fil dans les réseaux GSM
Dans notre étude, nous supposerons que le réseau GSM transporte uniquement des conversations vocales. Le transport de données sera pris en compte lors de l’étude des réseaux UMTS.
Les stations fixes GSM peuvent avoir une portée d’une dizaine de kilomètres. Cependant, le facteur principal limitant la taille d’une cellule n’est pas la portée des stations fixes mais le nombre de canaux de fréquence dont dispose l’opérateur mobile.
En effet, chaque canal permettant de satisfaire un certain nombre de conversations simultanées, le nombre de canaux disponibles détermine le nombre de conversations pouvant être simultanément gérées par cellule.
C’est donc souvent la densité d’utilisateurs qui déterminera le rayon des cellules. D’autre part, pour des raisons d’interférences entre cellules, toutes les fréquences ne peuvent être utilisées dans toutes les cellules. L’opérateur va donc déterminer un canevas selon lequel il attribuera les fréquences aux cellules. Ce canevas comportera un certain nombre de cellules et chaque fréquence ne sera utilisée qu’une seule fois par canevas83.
Nous supposerons par la suite, que l’opérateur mobile utilise un canevas de quatre cellules entre lesquelles les fréquences disponibles sont également réparties. La figure n°28 représente un tel canevas.
Figure n°28: Canevas cellulaire à 4 cellules
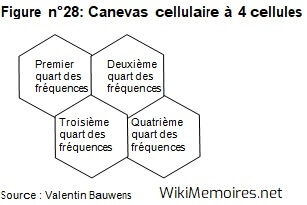
Source : Valentin Bauwens
Afin d’optimiser le ratio de réutilisation des fréquences par unité de surface sans augmenter les interférences entre cellules, les opérateurs utilisent souvent des antennes directionnelles qui permettent de segmenter les cellules en secteurs utilisant des fréquences différentes.
Par la suite, nous supposerons que chaque cellule est découpée en trois secteurs parmi lesquels les fréquences de la cellule sont réparties de façon égale. Chaque canevas de cellules est donc réparti en 12 secteurs que partagent 4 cellules.
La bande de fréquence dont dispose un opérateur n’est pas illimitée. Celle-ci doit en effet être achetée auprès de l’organe régulateur des fréquences. En ce qui concerne les technologies GSM, deux bandes de fréquences peuvent être utilisées: une à 900 Mhz et l’autre à 1800 MHz84.
Selon un professionnel de l’IBPT, l’organe belge régulateur des fréquences, il est de pratique courante chez les opérateurs d’acheter une douzaine85 de MHz par bande de fréquence. Historiquement, ceux-ci ont commencé par utiliser les fréquences autour de 900 MHz pour ensuite passer en 1800 MHz lorsque leurs réseaux ont saturé.
Nous étudierons donc deux situations: celle d’un opérateur utilisant 12 MHz de fréquence dans la bande de 900 MHz et celle d’un opérateur utilisant 12 MHz dans la bande de 900 MHz et 12 autres MHz dans la bande de 1800 MHz.
La technologie GSM utilisant 200 KHz par canal, 5 canaux peuvent être exploités par MHz. D’autre part, chaque canal peut gérer simultanément 8 communications et chaque communication demande une bande passante de 12 Kbps86. Notons également que même si un secteur peut théoriquement assurer un certain nombre de communications simultanées, ce chiffre ne sera jamais atteint en pratique. En effet, lorsqu’un canal se libère, il faudra toujours un certain temps avant qu’il soit à nouveau utilisé.
Au plus l’opérateur désire réduire la probabilité qu’un appel soit refusé par manque de lignes disponibles, au plus il devra prévoir des lignes en excès de la demande, pour que quelques lignes soient libres à tout moment.
Cette règle est formalisée par la loi de Erlang qui prédit la demande effective de communications simultanées pouvant être satisfaite à partir du nombre de lignes offertes et de la probabilité désirée qu’un appel soit refusé. Un graphique représentant cette loi est disponible en annexe n°10.
L’unité utilisée pour décrire la densité de la demande de communications simultanées est le Erlang/km². Il correspond au nombre d’heures de communications demandées pendant une certaine période de temps sur une surface de 1 km². Généralement les Erlang/km² sont exprimés sur une période d’une heure pendant l’heure de pointe.
Les règles précédemment décrites nous permettent de calculer le nombre de communications pouvant être simultanément gérées par cellule et donc, en fonction de la densité de la demande de communications simultanées, le rayon maximal de cette cellule. Le Tableau n°47 montre les calculs effectués dans le cas d’un opérateur disposant de une et de deux bandes de fréquence de 12 MHz.
Tableau n°47: calcul du nombre de communications GSM simultanées
| 12 MHz | 2 x 12 MHz | |
| Canaux | 60 canaux | 120 canaux |
| Canaux par cellule | 15 canaux | 30 canaux |
| Canaux par secteur | 5 canaux | 10 canaux |
| Appels théoriques par secteur | 40 appels | 80 appels |
| Appels effectifs par secteur selon la loi d’Erlang avec une probabilité de blocage de 1% | 30 Erlang | 65 Erlang |
| Erlang / Cellule | 90 Erlang | 195 Erlang |
| Mbps / Cellule | 1,08 Mbps | 2, 34 Mbps |
Source : calculs personnels
Remarquons que la bande passante requise par cellule est largement inférieure à la capacité du lien optique de la bande passante la plus faible (10 Mbps).
Selon un professionnel des télécoms87, les opérateurs mobiles implémentent la plupart du temps les connexions entre les stations fixes et le contrôleur de stations fixes sous forme d’un réseau en étoile. Cela signifie que chaque station fixe dispose d’une connexion individuelle qui la relie au contrôleur de stations fixes. Pour cela ils utilisent généralement des lignes louées à quelques Mbps. La figure n°29 A) illustre cette situation.
L’utilisation de liens optiques de capacité beaucoup plus élevée nécessiterait de modifier l’organisation de ces connexions et de passer à une architecture en forme de boucle. La Figure n°29 B) illustre ce type d’architecture. Afin de ne pas complexifier nos calculs, nous poserons l’hypothèse que tous les liens faisant partie de la boucle offrent la même capacité88.
La bande passante nécessaire pour les dispositifs d’une boucle serait alors égale à celle requise par cellule multipliée par le nombre de cellules desservies par la boucle. D’autre part, cette architecture en boucle permettrait d’atteindre des plus grandes distances à partir du contrôleur de stations fixes.
Figure n°29: Réseaux en étoile et en boucle
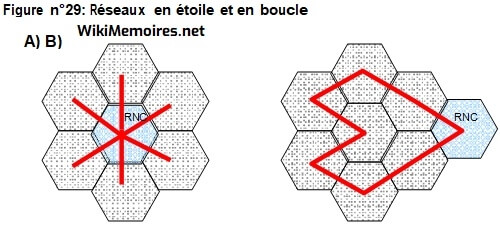
Rappelons que le nombre maximal de stations fixes connectées à un même contrôleur de stations fixes est de 64. Nous avons calculé que les réseaux GSM à 12 et 24 MHz nécessitent une bande passante par cellule respective de 1,08 et 2,34 Mbps. Supposons que l’opérateur prévoit une bande passante plus grande par cellule pour tenir compte de la croissance future de la demande et qu’il prévoit 1,5 et 3 Mbps par cellule pour les réseaux à 12 et 24 MHz respectivement89.
Ayant posé ces hypothèses, nous pouvons contrôler le nombre de cellules devant être desservies par la boucle optique pour que les dispositifs de cette boucle ne soient pas en sous capacité. Le tableau n°48 illustre ce nombre pour les dispositifs des différentes bandes passantes.
Tableau n°48: Cellules desservies par boucle en fonction de la bande passante des dispositifs OSF (technologie Optique Sans Fil) utilisés dans cette boucle.
| Bande passante | 12 MHz | 2 X 12 MHz |
| 10 Mbps | 6 | 3 |
| 50 Mbps | 33 | 16 |
| 155 Mbps | 103 | 51 |
| 622 Mbps | 414 | 207 |
| 1250 Mbps | 833 | 416 |
| 2500 Mbps | 1666 | 833 |
Source : Calculs personnels
Nous pouvons déjà exclure l’utilisation de boucles de liens optiques à 622, 1250 et 2500 Mbps, comme elles devraient desservir beaucoup plus que 64 cellules pour ne pas être en sous-capacité. En ce qui concerne les liens à 155 Mbps, ils pourraient uniquement être exploités dans un réseau GSM utilisant 24 MHz de largeur de bande.
Afin de vérifier si l’implémentation en boucle de liens OSF (technologie Optique Sans Fil) à 10, 50 et 155 Mbps pour connecter des stations fixes à un contrôleur de stations fixes est techniquement possible et économiquement justifiable, il convient de contrôler si les conditions suivantes sont remplies:
- – La densité de la demande est suffisante sur une superficie suffisamment grande
- – Les coûts par minute vendue sont suffisamment faibles
a) Condition de densité de demande suffisante sur une superficie suffisamment grande
Si la demande de communications simultanées par km² est relativement faible, le rayon d’une cellule devra être grand pour que la capacité de sa station fixe soit totalement exploitée.
Dans le cas où des stations fixes sont reliées entre elles par une boucle de liens optiques, le rayon des cellules ne pourra pas dépasser une certaine valeur au-delà de laquelle la distance entre deux stations fixes deviendra supérieure à la portée des dispositifs OSF. Tentons de déterminer, pour les dispositifs de chaque bande passante, la densité de la demande minimale qui rend la distance entre deux stations fixes compatible avec la portée de ces dispositifs.
Ayant calculé que la capacité d’une cellule est respectivement de 90 et de 195 Erlang pour les réseaux à 12 et à 24 MHz, nous pouvons trouver, en fonction de la densité de la demande en Erlang/km², le rayon de la cellule qui assure sa pleine capacité de la station fixe.
A partir de ce rayon peut être calculée la portée requise du lien OSF (technologie Optique Sans Fil) reliant deux stations fixes. La figure n°30 illustre la relation entre la densité de la demande et la portée requise du lien.
Figure n°30: Relation entre la densité de la demande et la portée requise du lien
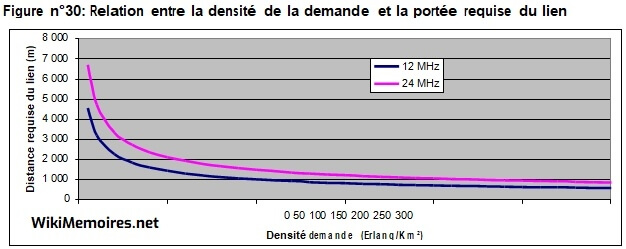
Source : calculs personnels
A partir de la relation représentée par la Figure n°30, nous pouvons calculer en fonction de la portée compétitive90 des dispositifs OSF (technologie Optique Sans Fil), la densité de la demande minimale permettant de ne pas dépasser cette portée. Ces distances sont montrées dans le Tableau n°49.
Tableau n°49: Densité d’utilisateurs minimale pour l’implémentation de liens OSF dans des conditions de compétitivité par rapport aux faisceaux hertziens.
| Bande passante | Distance compétitive | 12 MHz | 24 MHz |
| 10 Mbps | 4000 m | 7 Erlang/km² | 15 Erlang/km² |
| 50 Mbps | 2500 m | 17 Erlang/km² | 37 Erlang/km² |
| 155 Mbps | 2000 m | 57 Erlang/km² |
D’autre part, il ne suffit pas que la densité de la demande soit suffisamment importante dans une seule cellule. Il faudrait en effet trouver un endroit où elle le soit en moyenne sur un nombre suffisant de cellules adjacentes. La superficie requise pour une boucle peut être trouvée en multipliant le nombre de cellules par boucle, tel que déterminé dans le tableau n°48, par la superficie des cellules calculée en fonction de la densité de la demande.
Les tableaux n°50, 51 et 52 contiennent les résultats de ces calculs pour les dispositifs de 10, 50 et 155 Mbps respectivement. Les cases grises correspondent à des situations où l’OSF (technologie Optique Sans Fil) est exclu car la densité de la demande définie dans le tableau n°49 n’est pas atteinte.
Remarquons qu’il n’y a pas de grande différence dans ces résultats entre les réseaux utilisant 12 et 24 MHz de fréquence. Dans les réseaux à 24 MHz, les cellules sont deux fois plus grandes, mais la boucle parcourt deux fois moins de cellules.
Tableau n°50: Superficie requise pour une boucle de liens OSF (technologie Optique Sans Fil) à 10 Mbps en fonction de la densité de la demande et de la largeur de la bande de fréquence disponible.
| MHz disponibles | Stations fixes | 10 Erlang/km² | 20 Erlang/km² | 40 Erlang/km² | 60 Erlang/km² | 120 Erlang/km² | 200 Erlang/km² |
| 12 | 6 | 54 km² | 27 km² | 14 km² | 9 km² | 5 km² | 3 km² |
| 24 | 3 | / | 29 km² | 15 km² | 10 km² | 5 km² | 3 km² |
Tableau n°51: Superficie requise pour une boucle de liens OSF à 50 Mbps en fonction de la densité de la demande et de la largeur de la bande de fréquence disponible.
| MHz disponibles | Stations fixes | 10 Erlang/km² | 20 Erlang/km² | 40 Erlang/km² | 60 Erlang/km² | 120 Erlang/km² | 200 Erlang/km² |
| 12 | 33 | / | 149 km² | 74 km² | 50 km² | 25 km² | 15 km² |
| 24 | 16 | / | / | 78 km² | 52 km² | 26 km² | 16 km² |
Tableau n°52: Superficie requise pour une boucle de liens OSF (technologie Optique Sans Fil) à 155 Mbps en fonction de la densité de la demande.
| MHz disponibles | Stations fixes | 10 Erlang/km² | 20 Erlang/km² | 40 Erlang/km² | 60 Erlang/km² | 120 Erlang/km² | 200 Erlang/km² |
| 24 | 51 | / | / | / | 165 km² | 83 km² | 49 km² |
Comparons à présent ces résultats avec des données réelles concernant la répartition géographique de la densité de la demande dans une métropole type. Pour des raisons de confidentialité stratégique, il est assez difficile d’obtenir des statistiques précises de ce genre.
Un professionnel expérimenté91 travaillant auprès d’un opérateur belge a cependant bien voulu nous fournir quelques ordres de grandeur de la répartition géographique de la densité de la demande en Belgique.
La figure n°31 et le tableau n°53 décrivent les densités de la demande que l’on peut trouver dans les alentours de la ville de Bruxelles pendant les heures de pointe. Remarquons qu’il est important d’utiliser des données relatives aux heures de pointe, car ce sont elles qui déterminent le dimensionnement du réseau. En dehors des heures de pointe, le réseau sera en sous-capacité.
Figure n°31: Densité de la demande autour de la ville de Bruxelles (Erlang/km²).
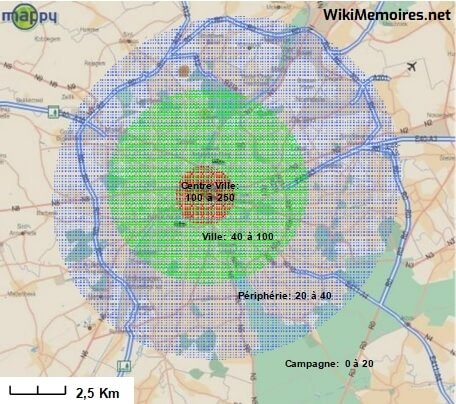
Tableau n°53: Description des segments de la figure numéro n°31
| Couleur | Délimitation | Appellation | Erlang/km² | Superficie92 |
| Brun | Petite ceinture | Centre-ville | 100 à 250 | 5 km² |
| Vert | Grande ceinture | Ville | 40 à 100 | 45 km² |
| Bleu | Ring | Périphérie | 20 à 40 | 127 km² |
Regardons si les conditions de densité de la demande suffisante sur une superficie suffisamment grande sont remplies pour les dispositifs de bandes passantes différentes.
– Les lien OSF (technologie Optique Sans Fil) à 10 Mbps ont besoin, dans les réseaux utilisant 12 MHz, d’une densité de la demande d’au moins 7 Erlang/km² sur une superficie d’environ 60 km². Comme la densité de la demande en campagne varie entre 0 et 20
Erlang/km² sur des grandes étendues, les dispositifs à 10 Mbps pourraient probablement y être utilisés dans des réseaux à 12 MHz. Dans les réseaux à 24 MHz, par contre, une densité d’au moins 15 Erlang/km² est requise sur une supérficie d’une 40aine de km², ce qui sera dur à trouver en campagne.
Par contre, en périphérie, où la densité varie entre 20 et 40 Erlang/km², les boucles constituées de liens optiques à 10 Mbps auront besoin d’une superficie comprise entre 15 et 30 km², ce qui est bien inférieur à la surface de la zone périphérique de Bruxelles. Ces boucles pourront donc y être utilisées. A fortiori, les dispositifs à 10 Mbps conviendront également à l’utilisation dans la ville et le centre-ville93.
– Les lien 0SF à 50 Mbps, utilisés dans un réseau à 12 MHz, ont besoin d’une densité d’au moins une 20aine d’Erlang/km² sur une superficie de 140 km². Pour les réseaux à 24 MHz, les densités de la demande doivent être supérieures à 40 Erlang/km² sur une superficie de 75 km². Ceci rend l’utilisation de boucles de liens à 55 Mbps impossible en campagne, où la densité varie entre 0 et 20 Erlang/km².
Ces liens pourraient par contre être utilisés en périphérie, mais uniquement dans des réseaux à 12 MHz. En effet, comme la densité de la demande y tourne autour de 30 Erlang/km², une boucle d’un réseau à 12 MHz couvrirait une surface d’une 100aine de km², inférieure à celle de la périphérie bruxelloise.
En ville, où la densité tourne autour de 70 Erlang/km², la surface couverte par une boucle serait juste supérieure à 40 km², ce qui correspond exactement à la superficie de la ville. Les dispositifs à 55 Mbps pourraient donc y être utilisés. A fortiori, les dispositifs à 55 Mbps conviendront également à l’utilisation dans le centre-ville94.
– Les liens OSF (technologie Optique Sans Fil) à 155 Mbps ont besoin d’une densité de la demande d’au moins 57 Erlang/km² sur une superficie d’environ 170 km², ce qui ne se retrouve nulle part en Belgique. Nous pouvons donc exclure l’utilisation de liens à 155 Mbps dans un réseau GSM.
Tableau n°54: Synthèse des résultats
| 10 Mbps | 50 Mbps | 155 Mbps | |
| Campagne | 12 MHz seulement | r | r |
| Périphérie | a | 12 MHz seulement | r |
| Ville | a | a | r |
| Centre ville | a | a | r |
b) Coût par minute
Essayons maintenant de dégager le coût de revient des liens OSF (technologie Optique Sans Fil) par minute de conversation vocale vendue. Pour cela Il faut calculer le nombre de minutes vendues par Erlang de capacité du réseau. Rappelons que lorsque nous parlions précédemment de la densité de la demande par km², il s’agissait de la demande au moment de l’heure de pointe. Nous ne pouvons donc pas en déduire directement le nombre de minutes vendues par an.
Supposons donc la répartition de la demande au cours de la journée par rapport à la demande à l’heure de pointe, telle que représentée sur la Figure n°32. Celle-ci a été déduite de conversations avec des professionnels95.
Figure n°32: Répartition de la demande au cours de la journée par rapport à la demande à l’heure de pointe.
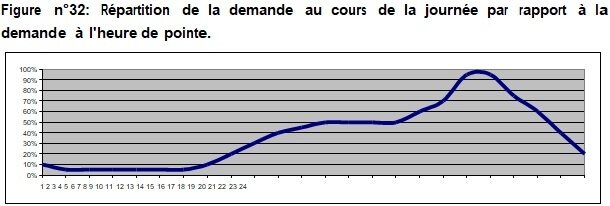
Informations : Nicolas Parmentier / Réalisation : Valentin Bauwens
Nous pouvons calculer à partir de cette figure que l’utilisation moyenne de la capacité est d’environ 40%. Il suffit donc de multiplier par 40% le nombre d’Erlang pouvant être desservis par dispositif96 à l’heure de pointe pour obtenir le nombre moyen d’Erlang vendus par dispositif.
Nous multiplions ensuite ce nombre par le nombre de minutes contenues dans une année pour obtenir le nombre de minutes vendues par dispositif et par an. En connaissant les coûts annuels équivalents des dispositifs optiques tels qu’ils sont calculés à la fin du deuxième chapitre, nous pouvons en déduire le coût par minute de conversation vendue.
Les résultats sont disponibles dans le tableau n°55 pour les dispositifs que nous n’avons par exclus précédemment. Remarquons que ces coûts ne varient pas en fonction de la densité de la demande par km², le rayon de cellules ayant été calculé de façon à ce qu’elles recouvrent un nombre constant d’Erlangs.
Tableau n°55: Coût de revient des liens OSF (technologie Optique Sans Fil) par minute de conversation vendue (en Cent par minute) pour les réseaux disposant de 12 et 24 MHz de fréquence
| BANDE PASSANTE | 12 MHz | 24 MHz |
| 10 | 0,078 | 0,041 |
| 50 | 0,091 | 0,043 |
Source : Calculs personnels
Nous pouvons constater que:
– Lorsque la largeur de la bande de fréquence utilisée double, le prix est environ divisé par deux. Ceci provient du fait que les réseaux à 12 MHz sont constitués de deux fois plus de cellules deux fois plus petites, le nombre de liens reliant ces cellules sera donc doublé.
– Lorsqu’on utilise des dispositifs de bande passante plus élevée, le prix par minute offerte augmente proportionnellement au coût annuel équivalent du dispositif.
En effet, l’utilisation de liens de plus grande bande passante ne permet que de multiplier le nombre de cellules desservies par boucle, sans beaucoup changer le nombre d’Erlang par dispositif. Il est donc plus avantageux de choisir le dispositif à 10 Mbps.
Notons que le nombre de cellules desservies par la boucle est inférieur d’une unité par rapport au nombre de liens composant la boucle, comme une des cellules traversées se trouve au même endroit que le contrôleur de stations fixes
Comparons ces coûts aux revenus par minute d’un opérateur GSM. Si nous observons les prix en vigueur en Belgique tels qu’établis par un comparatif de speed.be, disponible en Annexe n°9, nous constatons qu’à l’exception d’un opérateur, tous les opérateurs belges demandent une rémunération d’au moins 10 cents par minute. Le coût de revient par minute de la connexion entre la station fixe et le contrôleur de stations fixes varierait alors entre 0,4 et 0,9% du revenu par minute.
c) Conclusion GSM
Après avoir déterminé la capacité des cellules GSM en communications simultanées ainsi que leurs besoins en terme de bande passante, nous avons calculé les densités minimales de la demande ainsi que les superficies minimales devant afficher ces densités rendant possible l’utilisation de liens optiques pour transporter les données entre les stations fixes et les contrôleurs de stations fixes.
Nous avons ensuite comparé ces caractéristiques requises de l’environnement avec des statistiques réelles de la répartition géographique de la densité de la demande autour de la ville de Bruxelles.
Nous avons étudié le cas de deux types d’opérateurs: ceux qui disposent de 12 MHz de fréquence et ceux qui en utilisent 24 MHz
Selon nos calculs, seuls les liens optiques à 10 et 50 Mbps pourraient être employés pour relier les stations fixes et les contrôleurs de stations fixes. Par contre, l’utilisation des dispositifs de bande passante plus élevée nécessiterait des densités d’utilisateurs trop grandes sur des superficies trop importantes.
Les opérateurs utilisant 12 MHz de fréquence devraient pouvoir se servir du dispositif à 10 Mbps dans tous les types d’environnements. L’utilisation du dispositif à 50 Mbps ne serait par contre pas autorisée en campagne.
En ce qui concerne les opérateurs utilisant 24 MHz de fréquence, ils ne pourraient pas employer les liens optiques à 10 Mbps à la campagne et l’utilisation de dispositifs à 50 Mpbs ne leur serait autorisée qu’en ville.
L’analyse des coûts de revient des dispositifs 0SF nous a amenés à conclure que ceux-ci devraient rester inférieurs à 1 % des revenus qu’ils contribuent à générer, ce qui ne devrait pas avoir d’effet négatif sur la rentabilité de l’opérateur.
__________________________________
83 Viinikainen A. (octobre 2003), « The cellulal concept – System design fundamentals »
84 Aux Etats-Unis, une bande de fréquences autour de 1900 MHz est également utilisée
85 Il s’agit en fait de 2 x 12 MHz, 12 MHz étant utilisés pour les communications du l’unité mobile vers l’unité fixe et les autres 12 MHz pour les communications de l’unité fixe vers l’unité mobile.
86 Rysavy Research (novembre 2002), « Data capabilities for GSM Evolution to UMTS »
87 Nicolas Parmentier, Belgacom
88 Les liens optiques les plus éloignés du BSC pourraient avoir une capacité inférieure, mais ceci limiterait les capacités de redondance de la boucle.
89 Cette croissance future serait soutenu par l’acquisition de nouvelles fréquences
90 Les portées compétitives des dispositifs OSF, calculées à la fin du deuxième chapitre, sont les distances en dessous desquelles ils sont compétitifs par rapport aux faisceaux hertziens.
91 Vincent Bultot, Proximus
92 La superficie de la ville ne comprend pas celle du centre ville et la superficie de la périphérie ne comprend pas celle de la ville et du centre-ville
93 Pour affirmer qu’un dispositif est adéquat pour être utilisé dans une zone déterminée, nous permettons bien entendu que la surface couverte par la boucle déborde dans les zones adjacentes de densité inférieure.
94 Pour affirmer qu’un dispositif est adéquat pour être utilisé dans une zone déterminée, nous permettons bien entendu que la surface couverte par la boucle déborde dans les zones adjacentes de densité inférieure
95 Nicolas Parmentier, Belgacom
96 Le nombre d’Erlangs pouvant être desservis par dispositif est calculé en divisant le nombre d’Erlangs desservis par une boucle par le nombre de liens composant cette boucle. Le nombre d’Erlangs desservis par boucle est quant à lui obtenu en multipliant la capacité d’une cellule par le nombre de cellules desservies par la boucle.