Mécanique quantique et mouvement brownien

Mécanique quantique et mouvement brownien – 4° Partie :

4.1. Introduction

La mécanique quantique est née d’expériences ayant mis la théorie classique de la matière de Rutherford en défaut. Diverses expériences ont montré les contradictions de cette théorie, comme la démonstration de la nature ondulatoire de la matière. Selon le principe de falsification, les scientifiques ont donc dû introduire une nouvelle théorie plus générale : la mécanique quantique.
L’avènement en 1922 de la mécanique quantique fût une révolution dans la manière de fonctionner des sciences. Tout d’un coup, nous passions d’une façon déterministe d’envisager le monde à une façon probabiliste.
Plus troublant encore, contrairement à ce qui est demandé à toute science par le courant positiviste, la mécanique quantique n’a pas pour objet d’expliquer les phénomènes qu’elle étudie mais uniquement de les mesurer et de les prévoir. Pour mieux comprendre cette affirmation, il faut définir ce que l’on entend par «expliquer». Jusque là, en science, expliquer signifiait donner une théorie qui permettait de relier un évènement à ses causes de façon univoque. En mécanique quantique, ce n’est pas le cas pour deux raisons :
– Il n’y a pas de lien causal d’un évènement à un autre mais un lien probabiliste. C’est à dire qu’à partir d’une cause, il peut y avoir plusieurs effets et le même effet peut survenir de plusieurs causes différentes. La relation n’est donc pas univoque.
– Il faudrait aussi pouvoir observer expérimentalement la cause du phénomène pour pouvoir valider ou non la théorie. Or dans le cadre de la mécanique quantique, il est possible que les observations expérimentales soient biaisées par l’utilisation des outils d’observation.
En effet, comme nous travaillons sur des phénomènes infiniment petits, nous ne pouvons appréhender ceux-ci par l’expérience directe de nos sens. Nous sommes donc réduit à nous fier à des appareillages de mesures qui, au mieux, perturbent les phénomènes à étudier et, au pire, les provoquent. Dès lors, ne sachant pas «voir» ce qui se passe réellement, nous en sommes réduit à faire des suppositions pour la partie explicative. La mécanique quantique se contente de mesurer et de prédire ce qui peut se passer. On imagine donc assez bien l’émoi épistémologique que l’émergence d’une telle science a pu produire. En effet, comment considérer une science qui se construit avec des raisonnements d’une pureté mathématique tout en se basant sur la nature mais qui n’en explique rien. Alors qu’il était considéré jusqu’alors que le but ultime de la science était bien d’expliquer les lois de la nature

4.1.1. Principe d’incertitude de Heisenberg

A l’échelle de l’atome, toute tentative d’observation modifie l’état des atomes. On ne peut donc pas découpler l’observation du phénomène observé. A l’échelle atomique, les deux forment un couple indissociable car l’un influe sur l’autre.
Le principe d’incertitude de Heisenberg postule qu’il est impossible de connaître en même temps la position d’une particule et sa vitesse. On peut déterminer soit l’un soit l’autre mais pas les deux en même temps. Cette incertitude s’exprime par la formule suivante :
Où représente l’incertitude sur la position,  représente l’incertitude sur la vitesse et  est une constante.
Etant donné que les deux incertitudes se multiplient l’une l’autre et que le produit doit être supérieur à une constante, on voit bien qu’il est impossible d’obtenir une incertitude proche de zéro sur les deux composantes.
Ceci implique qu’on ne puisse connaître véritablement le comportement d’une particule et qu’on soit réduit à travailler sur des probabilités.

4.1.2. Le chat de Schrödinger

(Source : Alfred, Sauvons le chat de Schrödinger, 4/06/06, URL : www.vulgum.org/spip.php?article1078, page consultée le 18/07/08.)
Pour illustrer certains phénomènes étranges de la mécanique quantique, Schrödinger a inventé une expérience de pensée qui consistait à enfermer un chat dans une boite fermée. On installe aussi dans cette boite un élément radioactif et un compteur Geiger qui a 50% de chance sur une minute de faire tomber un marteau sur une fiole de cyanure qui tuerait le chat.
Après une minute d’expérience, il est impossible de savoir si le chat est mort ou vivant sans ouvrir la boite. Donc, sans avoir ouvert la boite et réalisé une observation, le chat est à la fois mort et vivant. Il possède les deux états en même temps.
En fait ce paradoxe illustre très bien ce que ce sont les probabilités. Quand on a une pièce de monnaie, on sait qu’elle a 50% de chances de tomber sur pile et 50% de tomber sur face mais on ne sait pas sur quelle face elle va tomber avant d’en faire l’expérience. Donc avant de lancer la pièce, celle-ci est à la fois pile et à la fois face. On ne sait absolument pas déterminer quel évènement va survenir lorsque l’on va lancer la pièce, on n’en connaît juste que les possibilités. Et c’est ce paradoxe qui illustre le fait qu’on ne puisse pas aborder la science comme une discipline déterministe où l’on peut déterminer un état à un moment en connaissant les états initiaux et les lois qui régissent ces états. La mécanique quantique nous plonge dans un monde probabiliste où un évènement peut en engendrer plusieurs différents selon certaines probabilités. Le monde n’est donc plus un enchaînement de causes et d’effets déterminés qui se déroulent sur la ligne du temps.

4.1.3. Le rôle de l’observateur et l’impossibilité d’un modèle prédictif certain de valorisation d’actions.

Dans les deux paragraphes précédents, nous avons vu que le rôle de l’observateur est crucial dans la théorie de la mécanique quantique. Selon Heisenberg, celui-ci perturbe les expérimentations et les mesures et donc fait partie du processus d’observation. Dans l’exemple du chat de Schrödinger, c’est l’observateur qui détermine le résultat de l’expérience. Avant d’ouvrir la boite, on ignore tout de l’état du système.
Ceci nous inspire une réflexion à propos de la possibilité d’existence d’un modèle prédictif de valorisation d’action certain. Prenons la courbe du cours d’une action. Nous savons qu’elle est le résultat des transactions entre les acheteurs et les vendeurs sur un marché. Or ces mêmes acheteurs et vendeurs utilisent la courbe qu’ils créent eux-mêmes pour prendre leurs décisions de vente ou d’achat. Donc, comme en mécanique quantique, ils sont à la fois observateurs et acteurs de cette courbe.
Imaginons maintenant que nous puissions déterminer avec exactitude le cours d’une action sur une période assez longue. Nous définirions par la même occasion le comportement exact des vendeurs et des acheteurs pendant toute cette période. Tant que le modèle n’est pas rendu public, personne ne sait que c’est possible. Que se passera-t-il lorsque le modèle sera rendu public? Les différents acteurs vont probablement essayer de tirer profit des prédictions en essayant de battre le modèle. Ce faisant, les observateurs deviennent acteurs et vont donc influencer la courbe actuelle en fonction de la courbe prédite. Ils vont adopter des comportements qu’ils n’auraient pas eus s’ils avaient été livrés à eux mêmes et, ce faisant, ils vont probablement invalider le modèle. En cas de tendance haussière, plus personne ne voudra vendre et tout le monde voudra acheter, ce qui créera des problèmes de liquidité et donc qui accentuera la tendance. De même en cas de baisse, tout le monde voudra vendre et personne ne voudra acheter ce qui modifiera les courbes.
Poussons le raisonnement plus loin, imaginons que notre modèle fiable tienne compte des mouvements des acheteurs et des vendeurs par rapport à lui-même. Si les cours des actions sont totalement définis, il ne sert plus à rien de spéculer dessus. Dans ce cas, est-ce que le métier de trader existerait encore? Et surtout y aurait-il encore suffisamment d’acheteurs et de vendeurs sur le marché pour que le modèle puisse encore fonctionner ou bien ceux-ci disparaîtraient-ils, entraînant dans leur chute, la déficience de notre modèle qui ne pourrait plus exister faute d’acteurs/observateurs.
A la lueur de ce paradoxe, on comprend qu’il n’est pas possible de concevoir un modèle déterministe prédictif de valorisation d’actions fiable à 100%. Ce modèle contiendrait en lui les germes de son disfonctionnement. Mais, nous pouvons, comme en mécanique quantique, tenter la conception d’un modèle d’évaluation probabiliste.

4.1.4. Le fonctionnement du hasard : les distributions de probabilité.

Avant d’aller plus en profondeur dans notre exposé, nous allons détailler quelques principes de base sur la façon dont fonctionnent le hasard et les différentes distributions de probabilité.
Une distribution de probabilité sur un domaine discret est définie par une suite de probabilités (p1,…, pn) tels que les pi appartiennent à [0;1] et que . Une distribution de probabilité peut donc prendre plusieurs formes différentes. Nous sommes plutôt habitués à côtoyer des évènements qui ont la même probabilité d’arriver comme par exemple le lancé d’un dé où toutes les faces ont la même probabilité de sortir. Mais il existe aussi une infinité de distributions de probabilité où certains évènements ont plus de chance de survenir que d’autres.
Les lois du hasard sont bâties sur trois théorèmes mais peuvent varier en fonction de la validité de ces théorèmes.
1°) La loi des grands nombres qui nous dit que plus un échantillon est grand, plus sa moyenne converge vers l’espérance statistique. Et donc que l’espérance est la limite à l’infini de la moyenne.
2°) Le théorème central limite qui dit que la réduction d’une somme de variables aléatoires tend vers une distribution normale. Et son corollaire d’échelle selon lequel la somme de variables aléatoires distribuées normalement reste une distribution normale et donc qu’un échantillon d’un ensemble de valeurs distribuées normalement est aussi distribué normalement.
3°) Les données passées et futures sont indépendantes les unes des autres.
Selon Mandelbrot, il existerait plusieurs sortes de hasard dont le hasard Gaussien, décrit par la distribution normale, serait son expression la plus simple. Il y aurait selon lui, trois types de hasard qu’il qualifie de «bénin», «lent» ou «sauvage». Ces types de hasard auraient des distributions assez différentes.
– Le hasard bénin : l’exemple typique est la distribution normale qu’on peut reproduire rapidement et facilement avec un échantillon de données assez réduit. C’est le hasard qu’on maîtrise le mieux. C’est aussi la distribution la plus courante lorsqu’on observe les phénomènes physiques.
– Le hasard lent : on arrive à vérifier les trois théorèmes mais tellement lentement, avec un échantillon tellement grand qu’on a l’impression d’avoir à faire à un hasard sauvage si on se base sur le court ou le moyen terme. On pourrait représenter le hasard lent par une courbe de Gauss très aplatie, c’est-à-dire avec une variance très élevée.
– Le hasard sauvage : correspond à des distributions de probabilités qui ne répondent pas aux théorèmes énoncés ci-dessus et qui peuvent être caractérisées par de grands écarts par rapport à la norme qui peuvent rendre le calcul de moyenne totalement impossible. En fait, on peut y trouver une variance infinie ce qui rend la loi des grands nombres impossible à appliquer, puisqu’il n’y a pas de convergence.

4.2. Exemple de théorie de mécanique quantique : l’effet tunnel

Nous allons voir à travers cette application emblématique comment le fait d’utiliser une théorie probabiliste au lieu d’une théorie déterministe peut produire des effets étonnants et qui plus est, ces effets ont été vérifiés à maintes reprises.
Nous n’allons pas détailler ici les calculs car cela nécessiterait de développer des prérequis mathématiques assez lourds qui ne sont pas le propos de ce mémoire. Nous allons donc tenter de vulgariser au maximum.
Principe de l’effet tunnel : il s’agit de lancer une particule sur une barrière de potentiel. En mécanique classique, cette particule rebondirait sur la barrière et prendrait une trajectoire inverse. Il lui serait impossible de traverser cette barrière. Cependant, en mécanique quantique, il existe une probabilité non nulle pour que cette particule arrive à traverser cette barrière de potentiel.
Pour arriver à ce résultat, on pose un système de trois équations différentielles de Schrödinger qui décrivent les fonctions d’onde de la particule avant la barrière, dans la barrière et après la barrière. En résolvant ce système d’équations différentielles, on obtient comme résultat une probabilité strictement positive de passer de l’autre côté de la barrière. Cette probabilité est fonction de la taille de la barrière et de la quantité de mouvement de la particule. La probabilité de passer à travers décroît exponentiellement par rapport à la taille de la barrière. Il est donc possible à la particule de traverser cette barrière d’autant plus facilement que celle-ci est faible. Alors que cette possibilité n’existe pas en mécanique classique.

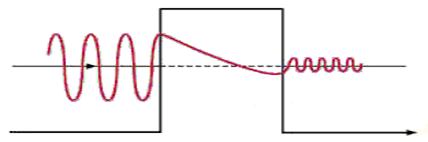
On appelle cela l’effet tunnel car la particule donne l’impression d’emprunter un tunnel pour traverser la barrière.
Lire le mémoire complet ==> (Comparaison épistémologique entre les modèles issus des sciences de la vie et les modèles de valorisation d’actions)
Mémoire présenté pour l’obtention du grade de Master en sciences commerciales
Enseignement supérieur de type long de niveau universitaire
Groupe ICHEC – ISC St-LOUIS – ISFSC – Haute Ecole