Le diagramme enthalpique de MOLLIER
I. 3. Le diagramme enthalpique de MOLLIER (Cf. annexe)
Le diagramme de Mollier permet de connaître l’état du réfrigérant en fonction de la pression et de l’enthalpie. Il a été déduit de la relation pression – température existant dans les gaz liquéfiables.
Ce diagramme porte en abscisses, l’enthalpie h en kJ/kg (contenu en énergie du fluide) et en ordonnées, la pression absolue P sur une échelle logarithmique en bars (10³ Pa).
Chaque fluide frigorigène possèdera donc un diagramme (log P, h) qui lui est propre.
D’une manière générale le diagramme enthalpique fait apparaître une zone de changement d’état où le fluide est à l’état diphasique. (Mélange liquide + vapeur)
A gauche, La courbe de liquide saturé où chaque point correspond à un état 100 % liquide et donc 0 % de vapeur. A droite, une courbe dite de vapeur saturée (100% vapeur et 0 % liquide).
L’intersection de ces deux courbes se réalise en un point sommet appelé point critique au-dessus duquel un changement d’état n’est plus possible.
La zone située dans l’enveloppe représente la zone hétérogène de mélange liquide/vapeur en changement d’état par exemple.
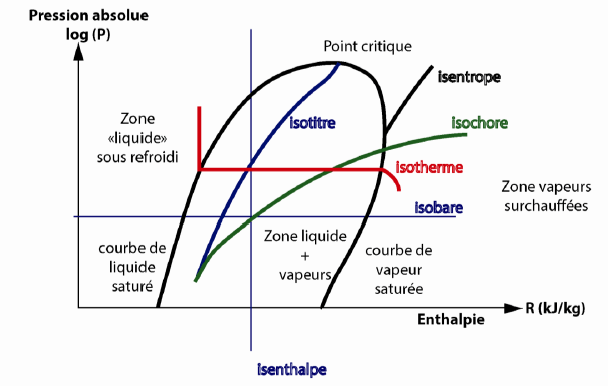
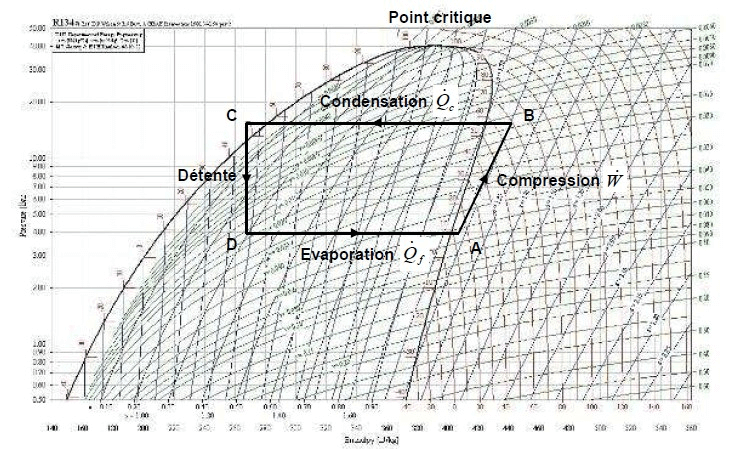
Figure 8 : Diagramme de Mollier
Le diagramme représente également :
* Les courbes à pourcentage de vapeur constant (de 0 à 1 ou de 0 à 100 %) dans la zone liquide/vapeurs.
* Les courbes :
- à volume spécifique V en m³/Kg (isochores)
- à entropie constante en kJ/kg.°K. (isentropes)
- à température constante. (isothermes)
- Les parallèles aux axes
- des abscisses sont les droites isobares où chaque point a la même pression,
- des ordonnées sont les droites isentropiques où chaque point a la même enthalpie.
Dans la zone liquide/vapeurs, les isothermes (lignes des points qui sont à la même température) sont confondues avec les isobares (lignes des points de même pression).
Ce qui renvoie à des lois thermodynamiques telles que : l’évaporation et la condensation se produisent à pression constante sans changement de température mettant en présence un mélange de liquide/vapeur durant le changement d’état physique.
Le diagramme enthalpique de MOLLIER permet donc sans calcul :
- de relever les paramètres physiques d’un fluide dans un état physique donné.
- de tracer le cycle fonctionnel d’une installation frigorifique pour un fluide déterminé en fonction des températures (ou pressions) d’évaporation et de condensation.
I.4. Influence des variations de température, à l’évaporateur et au condenseur, sur le fonctionnement de l’installation :
Dans le but de produire du froid, l’installation frigorifique interagit avec les milieux extérieurs : l’enceinte à refroidir et le milieu ambiant.
Ce qui signifie que la modification des paramètres extérieurs influe sur le fonctionnement de l’installation.
* Une augmentation de la température ambiante entraîne une augmentation de la température de condensation. Au niveau du condenseur cela s’explique par une production calorifique importante.
Le compresseur pour répondre à cette augmentation de température de condensation doit consommer une quantité d’énergie importante.
Ce qui implique une diminution des performances de l’installation autrement dit de son coefficient de performance.
Cependant, Une diminution de la température ambiante entraîne une diminution de la température de condensation.
Ce qui implique la diminution de la production calorifique au condenseur. Le compresseur travaille moins, ce qui améliore les performances de l’installation.
* Lorsqu’il y a diminution de la température de l’enceinte à refroidir, la température de vaporisation diminue.
Cela se traduit par une faible production frigorifique à l’évaporateur et une consommation de l’énergie importante au compresseur. Par conséquent, le coefficient de performance de l’installation diminue.
L’augmentation de la température de l’enceinte à refroidir entraîne une augmentation de la température de vaporisation.
L’évaporateur produit alors plus de froid et le compresseur consomme moins d’énergie. Ce qui par conséquent se traduit par l’amélioration du coefficient de performance de l’installation.
CHAPITRE III : RESULTATS ET ANALYSES
Résultats
III. 1. Evolution des coefficients des performances :
a. Réversible ou idéal de Carnot:
Variation du coefficient de performance de Carnot en fonction de la température dimensionnelle à l’évaporateur 0
Figure 14: Variation du coefficient de performance de Carnot en fonction de0
b. Irréversible, de l’installation réelle:
Variation du coefficient de performance de l’installation en fonction de la température adimensionnelle à l’évaporateur 0
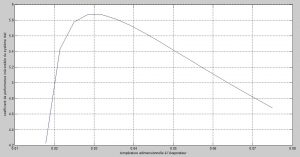
Figure 15: Variation du coefficient de performance de l’installation en fonction de0
2. Evolution de la puissance calorifique minimale adimensionnelle :
Variation de la puissance calorifique adimensionnelle en fonction de la température adimensionnelle à l’évaporateur 0
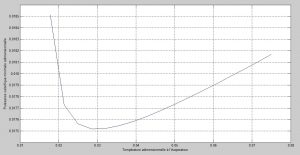
Figure 16: Variation de la puissance calorifique adimensionnelle en fonction de0
3. Evolution de la puissance mécanique minimale adimensionnelle :
Variation de la puissance mécanique minimale adimensionnelle en fonction de la temperature adimensionnelle à l’évaporateur .
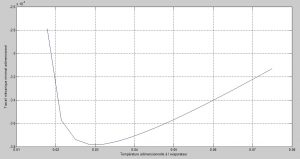
Figure 17: Variation de la Puissance mécanique minimale adimensionnelle en fonction de0
4. Evolution du rendement de l’installation par rapport au cycle de Carnot :
Variation du rendement en fonction de la température adimensionnelle à l’évaporateur 0
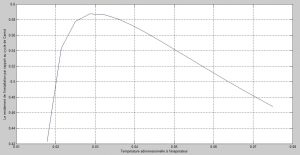
Figure 18:Variation du rendement en fonction de0
Analyse
Les graphiques tels que présentés ont pour abscisse la température adimensionnée à l’évaporateur, qui à chaque valeur correspond à une valeur de température adimensionnée au condenseur.
Pour des températures imposées aux réservoirs : évaporateur et condenseur, on constate que le Coefficient du cycle de Carnot de référence reste constant (figure 14), contrairement au coefficient de performance de l’installation réel qui présente pour sa part un maximum correspondant à un minimum de dépense énergétique (figure15).
Une situation qui correspond à des différences optimales de température 8,38 K et 9,8 K respectivement à l’évaporateur et au condenseur.
Ainsi, la puissance absorbée par le compresseur présente à cet instant une valeur minimale (figure 17) afin d’évacuer en permanence le flux de chaleur imposée pour le conditionnement d’air des locaux de la banque, correspondant au minimum de flux évacué au condenseur (figure 16).
Par ailleurs, c’est précisément pour ces mêmes valeurs que le rendement de l’installation présente un maximum (figue 18).
Par conséquent, aussi bien à l’évaporateur qu’au condenseur, un éloignement du fonctionnement de l’installation par rapport au point de consigne optimal dû à une augmentation ou une diminution de ces différences de température entraine une augmentation des pertes externes dues aux échanges thermiques et implicitement une réduction du rendement de l’installation.
Le régulateur, en l’occurrence le thermostat, interviendra pour corriger en temps réel l’apparition de l’écart de température par rapport au point de consigne optimal 8,38 K.
Conclusion :
Ce travail représente l’optimisation d’une installation frigorifique à compression mécanique des vapeurs.
L’installation frigorifique a été étudiée du point de vue thermodynamique autrement dit une attention particulière est accordée aux irréversibilités dues aux écarts de température aux niveaux des réservoirs : l’évaporateur et le condenseur.
Cette optimisation a eu pour but de prévoir les points de consigne nécessaires à l’élaboration d’un système permettant l’utilisation rationnelle de l’énergie dans les installations frigorifique.
Il faut noter que la rationalisation de l’énergie dans une installation se traduit par un travail minimal effectué par le compresseur.
Rappelons que l’installation frigorifique interagit avec les milieux extérieurs (le milieu à refroidir et le milieu extérieur) afin de produire du froid.
Par conséquent, la variation de température des milieux extérieurs influent le fonctionnement de l’installation implicitement sur le rendement de l’installation.
Au cours des processus d’échange avec les réservoirs de chaleur, les lois de transfert de chaleur nous ont permis, d’une part, d’exprimer la chaleur fonction de la conductance et des variations de température.
D’autre part, la méthode de la thermodynamique en temps fini met en évidence l’existence des différences optimales de température au niveau des réservoirs en transformant les grandeurs dimensionnées en grandeurs adimensionnées.
Notre étude a permis, une amélioration des performances de l’installation frigorifique de sorte que les variations de température des milieux extérieurs entraine à l’évaporateur une production frigorifique maximale, au condenseur, une production calorifique et un travail minimal au compresseur.
C’est précisément à cet instant que les écarts de température à l’évaporateur et au condenseur sont optimaux.
Le coefficient de performance déterminé est supérieur au coefficient de performance du l’installation réelle étudiée dans ce document.
Cette large différence de performance est due au fait que l’installation réelle présente, dans son fonctionnement, des irréversibilités interne (due aux frottements et aux pertes de charge) et externe (due aux différences de température).
Par contre, l’optimisation de l’installation réelle ne considère que les irréversibilités externes dues aux échanges thermiques.
Par ailleurs, une variation du fonctionnement de l’installation par rapport au point de consigne due à une augmentation ou une diminution des différences de température à l’évaporateur et au condenseur entraine une augmentation des pertes thermiques, par conséquent une diminution du rendement de l’installation.
De ce fait, le rôle du le régulateur (le thermostat) sera de corriger les différences de température au niveau de l’évaporateur et du condenseur par rapport aux points de consigne prévus.
GLOSSAIRE
– Thermodynamique :
C’est une discipline qui étudie des processus des machines, au cours desquels l’énergie est échangée sous forme de chaleur ou de travail mécanique
– Chaleur sensible:
C’est la quantité de chaleur qui provoque la variation de température d’un corps sans modifier son état physique.
– Chaleur latente:
C’est la quantité de chaleur qui provoque le changement d’état d’un corps sans modifier sa température.
– Chaleur latente massique de vaporisation:
C’est la quantité de chaleur qu’il faut fournir à 1 kg d’un corps pour le faire passer de l’état liquide à l’état gazeux sans élever sa température.
– Température critique ou pression critique:
C’est le point d’équilibre (relation pression température) au-dessus duquel on ne peut plus différentier la phase liquide de la phase gazeuse d’un même corps.
Aucune condensation n’est donc possible, le fluide est dit en l’état supercritique.
– La température d’ébullition:
Il s’agit de la température d’ébullition sous pression atmosphérique.
Cette température doit être telle que la pression dans le circuit reste supérieure à la pression atmosphérique, afin d’éviter les entrées d’air.
– Température catastrophique:
C’est la température maximale supportable par un fluide dans un circuit en présence d’huile et de cuivre.
Au-delà de cette température le fluide se décompose et forme des acides fluorhydriques et chlorhydriques.
– Coefficient de performance de Carnot
Le coefficient de performance limite d’un système énergétique fonctionnant dans des conditions de réversibilité.
– Coefficient de performance réel
Le rapport entre l’effet utile désiré et la dépense énergétique.
– Transformation thermodynamique réversible
Transformation qui conserve l’entropie (dénommée également transformation parfaite, idéale).
C’est une transformation inaccessible en pratique puisqu’elle nécessite une évolution selon une succession d’états d’équilibre (transformation quasi-statique), donc elle s’effectue en un temps infini.
– Transformation thermodynamique irréversible
Transformation réelle, entraînant la création d’entropie.
BIBLIOGRAPHIE
bibliographie-diagramme-enthalpique-MOLLIER
ANNEXES
Centrale à eau glacée
ANNEXE 1

Compresseur
Condenseur
Canalisation à eau glacée

Centre de traitement d’air appelé CTA
Conduit de reprise d’air dans les locaux de la banque


Diagramme de Mollier du fluide frigorigène R134a
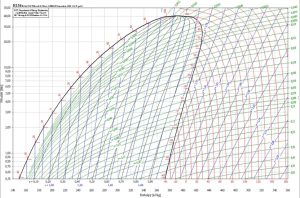
ANNEXE 2
Document technique de la centrale à eau glacée






Procédure de simulation sur MATLAB
* Evolution du coefficient de performance réversible de Carnot
| >> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0429 0.0464 0.0500 0.0571 0.0607 0.0643 0.0679 0.0714 0.0750]; | 0.0536 |
| >>a=x-x; >>b=a+1.1-1; | |
| >> y=1./b; >> plot(x,y); | |
| >>xlabel(‘température adimensionnelle à l’évaporateur’); >>ylabel(‘Coefficient de performance réversible de carnot’); | |
| >>grid |
* Evolution du coefficient de performance irréversible du système réel
| >> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0429 0.0571 0.0607 0.0643 0.0679 0.0714 0.0750] ; | 0.0464 | 0.0500 | 0.0536 |
| >> s=x-0.01497; >> k=x.*x; >> n=k./s; >> m=1-n; >> p=1.1./m; >> t=p-1; >> y=1./t; >> plot(x,y) >> xlabel(‘température adimensionnelle à l’évaporateur’); >> ylabel(‘coefficient de performance irréversible du système réel’); >>grid |
* Evolution du rendement de l’installation
>> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0429 0.0464 0.0500 0.0536
0.0571 0.0607 0.0643 0.0679 0.0714 0.0750] ;
>>s=x-0.01497;
>>k=x.*x;
>> n=k./s;
>> m=1-n;
>> p=1.1./m;
>>t=p-1;
>> y=1./t;
>>a=x-x;
>>b=a+1.1-1;
>> c=1./b;
>> f=y./c;
>> plot(x,f)
>>xlabel(‘Température adimensionnelle à l’évaporateur’);
>>ylabel(‘Le rendement de l’installation par rapport au cycle de Carnot’);
>>grid
* Evolution de la puissance calorifique minimale adimensionnelle
| >> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0429 0.0571 0.0607 0.0643 0.0679 0.0714 0.0750] ; | 0.0464 | 0.0500 | 0.0536 |
| >> a=x./0.01497; >> b=1./x; | |||
| >> c=1./0.01497; >> d=c-b-a; | |||
| >> e=1./d; >> f=0.01497./x; | |||
| >> g=1-f; >> h=1.1.*g; | |||
| >> j=h.*e; >> plot(x,j) | |||
| >>xlabel(‘Température adimensionnelle à l’évaporateur’); >>ylabel(‘Puissance calorifique minimale adimensionnelle’); | |||
| >>grid |
* Evolution du travail mécanique adimensionnel
| >> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0571 0.0607 0.0643 0.0679 0.0714 0.0750] ; | 0.0429 | 0.0464 | 0.0500 | 0.0536 |
| >> a=x./0.01497; | ||||
| >> b=1./x; >> c=1./0.01497; | ||||
| >>d=c-b-a; >> e=1./d; | ||||
| >> f=0.01497./x; >> g=1-f; | ||||
| >> h=1.1.*g; >>j=h.*e; | ||||
| >>k=j-0.0213; >> plot(x,k) | ||||
| >>xlabel(‘Température adimensionnelle à l’évaporateur’); >>ylabel(‘Travail mécanique minimal adimensionnel’); >>grid |