Chapitre 5: Première ébauche de la fonction de coût –
5.1 Introduction
Dans ce chapitre, nous présentons les premiers résultats de l’optimisation de la fonction de coût. Nous avons choisi pour cela un cas simple afin de donner une approche intuitive de cette fonction, ou en d’autres termes, une manière avec laquelle on peut pratiquement utiliser cette fonction. Nous exposons d’abord les simplifications, dont la forme finale de la fonction de coût dépendra. Ensuite, nous présenterons le programme optimum_access.c avec l’interprétation de ses résultats.
5.2 Objectifs et contraintes sur la fonction de coût
Pour la classe A, ou le service de voix, le critère important est la probabilité de blocage. Cette dernière n’est donc plus une contrainte comme on l’a d’abord suggéré, mais devient l’objectif à atteindre. Pour l’opérateur, il s’agit donc de réaliser le cahier des charges suivant :
- Objectif : minimiser Pbl
- Contraintes :
- QoS exigée par le client : Pcoupure d’appel bornée
- Les moyens limités du satellite en vue : Ncanaux (bande passante disponible)
Pour le service de la classe B ou service de données : il s’agit d’un cahier des charges analogue, le critère important étant le temps de latence, d’où ce cahier des charges devient :
- Objectif : minimiser le temps de latence
- Contraintes :
- QoS requise : Pperte de paquets bornée
- Les moyens du satellite limités en termes de capacité résiduelle
5.3 Considérations et approximations
D’une part, on considère que les données sont de même nature que la voix, c’est-à-dire :
- Le processus d’arrivée des données est de type Poisson
- Leur durée de service est la même que celle de la voix : de l’ordre de 2 minutes, d’où : μ = 0.5 min⁻¹
- Leur taux d’arrivée est du même ordre que celui de la voix. D’où, le taux d’arrivée au satellite λ est dans ce cas la somme des deux taux d’arrivée voix et données :
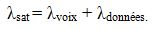
La probabilité de blocage, celle obtenue pour un système avec pertes (sans file d’attente), s’écrit donc par la Loi d’Erlang B comme suit :
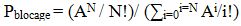
D’autre part, on considère qu’il s’agit d’un lien idéal, c’est-à-dire que :
- La probabilité de coupure d’appel due à un mauvais handover est nulle.
- La probabilité de pertes de paquets est, elle aussi, nulle.
5.4 Exemple d’optimisation de la fonction de coût
5.4.1 Contexte
Le client se trouve sous la couverture de deux satellites A et B caractérisés chacun par leurs taux d’arrivée λA et λB au moment où il fait sa demande, donc caractérisés par leurs taux de blocage respectifs donnés par le système suivant :
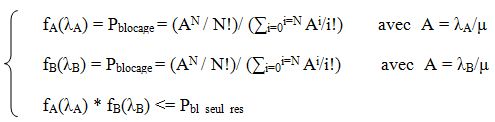
Il s’agit, dans ce cas, de choisir le satellite auquel rattacher la requête de ce client afin de minimiser la probabilité de blocage du réseau Pres qui est égale au produit des probabilités de blocage de chacun des satellites. (On note que Pbl_seul_res est la probabilité de blocage seuil choisie par l’opérateur comme paramètre de QoS).
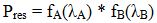
La solution Pres dépend évidemment du couple (λA, λB). Elle sera donc une surface formée par un ensemble de couples (λA, λB).
5.4.2 Remarques sur le code source et résultats
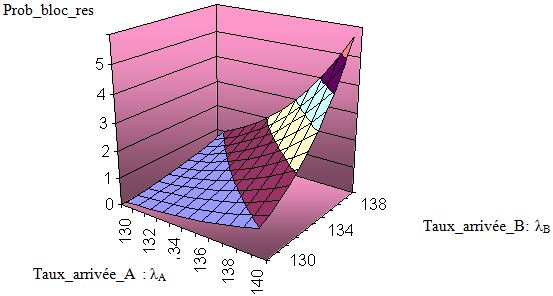
Note : le code source de optimum_access.c est présent dans l’annexe C. En itérant ce programme pour des valeurs de λB comprises entre 130 clients/min et 140 clients/min avec un pas de 1, on obtient les résultats regroupés dans le tableau C.1 fourni aussi dans l’annexe C. Pour obtenir la représentation graphique de la surface en 3D par le logiciel Excel, nous rassemblons les taux d’arrivée λA (en ligne) et λB (en colonnes) dans le tableau 5.1. Les valeurs obtenues sont celles de la Prob_bloc_res.
| t_arriveeA | |||||||||||
| t_arriveeB | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 |
| 130 | 0.170276 | 0.207485 | 0.251505 | 0.303299 | 0.363915 | 0.434483 | 0.516212 | 0.610389 | 0.718367 | 0.841564 | 0.981453 |
| 131 | 0.207485 | 0.252826 | 0.306465 | 0.369577 | 0.443439 | 0.529427 | 0.629017 | 0.743773 | 0.875347 | 1.025466 | 1.195923 |
| 132 | 0.251505 | 0.306465 | 0.371484 | 0.447986 | 0.537518 | 0.64175 | 0.762468 | 0.90157 | 1.061059 | 1.243026 | 1.449648 |
| 133 | 0.303299 | 0.369577 | 0.447986 | 0.540242 | 0.648212 | 0.773909 | 0.919487 | 1.087236 | 1.279569 | 1.499011 | 1.748183 |
| 134 | 0.363915 | 0.443439 | 0.537518 | 0.648212 | 0.777761 | 0.928579 | 1.103251 | 1.304526 | 1.535298 | 1.798596 | 2.097566 |
| 135 | 0.434483 | 0.529427 | 0.64175 | 0.773909 | 0.928579 | 1.108642 | 1.317186 | 1.55749 | 1.833012 | 2.147367 | 2.504311 |
| 136 | 0.516212 | 0.629017 | 0.762468 | 0.919487 | 1.103251 | 1.317186 | 1.564959 | 1.850466 | 2.177815 | 2.551303 | 2.975391 |
| 137 | 0.610389 | 0.743773 | 0.90157 | 1.087236 | 1.304526 | 1.55749 | 1.850466 | 2.18806 | 2.57513 | 3.016756 | 3.518213 |
| 138 | 0.718367 | 0.875347 | 1.061059 | 1.279569 | 1.535298 | 1.833012 | 2.177815 | 2.57513 | 3.030672 | 3.550422 | 4.140589 |
| 139 | 0.841564 | 1.025466 | 1.243026 | 1.499011 | 1.798596 | 2.147367 | 2.551303 | 3.016756 | 3.550422 | 4.159308 | 4.850686 |
| 140 | 0.981453 | 1.195923 | 1.449648 | 1.748183 | 2.097566 | 2.504311 | 2.975391 | 3.518213 | 4.140589 | 4.850686 | 5.656987 |
Table 5.1 – Variation de Pblocage-res en fonction des taux d’arrivée λA et λB
On obtient alors la surface suivante :
| λA \ λB | 130 | 131 | 132 | … | 140 |
|---|---|---|---|---|---|
| 100 | — | — | — | … | — |
| 110 | — | — | — | … | — |
5.4.4 Interprétation des résultats
On voit bien d’après la figure 5.1 que la probabilité de blocage du réseau varie dans le même sens que les taux d’arrivée λA et λB : elle augmente lorsque ces derniers augmentent. Les courbes parallèles au plan (λA, λB) représentent une même valeur de Pblocage-res pour différents couples (λA, λB).
L’opérateur fixe comme paramètre de QoS une valeur de Pblocage-res = Pblo-res-seuil. Lorsqu’un client fait une requête, il sera admis si le point (λA, λB) associé tombe en dessous de la surface limitée par Pbloc-res-seuil ; sinon, la requête sera rejetée.
5.5 Conclusion
Ainsi, ce chapitre nous a donné une idée sur l’application pratique de la fonction de coût à partir d’un exemple théorique. Dans les chapitres suivants, nous utiliserons les résultats de cette fonction dans des cas réels grâce au simulateur de réseau ns, qui permettra de simuler différentes situations.
FAQ 1: Quel est l’objectif de la fonction de coût pour le service voix (classe A) ?
L’objectif principal de la fonction de coût pour le service de voix est de réduire au maximum la probabilité de blocage des appels (Pbl). En d’autres termes, le réseau doit garantir que les utilisateurs de la voix puissent passer leurs appels avec un minimum de refus, tout en respectant les contraintes de qualité de service.
FAQ 2: Quelles contraintes encadrent le service de données (classe B) ?
Pour le service de données, la contrainte essentielle concerne la qualité de service (QoS). Le système doit assurer une perte de paquets limitée et respecter la capacité disponible du satellite. L’objectif est donc de minimiser le temps de latence tout en tenant compte des ressources réseau limitées.
FAQ 3: Comment est calculé le taux d’arrivée global au satellite λ ?
Le taux d’arrivée total au satellite, noté λ, est obtenu en additionnant les taux d’arrivée de la voix (λA) et des données (λB). Ce calcul permet de mesurer la charge globale supportée par le satellite et de déterminer la probabilité de blocage du réseau.
FAQ 4: Dans quelles conditions un client est-il accepté ou rejeté par le réseau ?
Un client est accepté par le réseau si son couple de taux d’arrivée (λA, λB) se situe en dessous du seuil de probabilité de blocage défini par l’opérateur (Pblo-res-seuil). Si ce seuil est dépassé, la requête est automatiquement rejetée afin de garantir la qualité de service (QoS) pour l’ensemble des utilisateurs.