Étude sur l’optimisation d’une installation frigorifique à compression mécanique par la thermodynamique en temps fini : maximisation du coefficient de performance, réduction de la consommation énergétique et amélioration des performances globales.
Université Marien Ngouabi
L’Ecole Nationale Supérieure Polytechnique
L’ENSP-UMNG
Mémoire d’ingénieur présenté pour l’obtention du diplôme d’ingénieur électromécanicien
Spécialité: Maintenance
Optimisation d’une installation frigorifique à compression mécanique des vapeurs par la méthode de la thermodynamique en temps fini
Par :
MOMBEKI PEA Hamir Johan
Encadreurs :
MISSETETE Alfred Raoul, MA OKOTAKA EBALE Louis
Date de soutenance :
Novembre 2015
Jury:
Président : BOSSOTO Guy Richard, Pr
Examinateurs : EDOURA GAENA Boris, MA MOUKANDI Guy
2014-2015
Introduction générale
CHAP I : Synthèse sur les installations frigorifiques….. 16
I.Généralités sur les installations frigorifiques.17
I.1. Principaux composants……17
I.2. Fonctionnement d’une installation frigorifique..18
I.2.1. Fluides frigorigènes..…21
I.2.2. Evaporateur..….24
I.2.3. Compresseur.27
I.2.4. Condenseur.….30
I.2.5. Détendeur..…33
I.3. Diagramme enthalpique de MOLLIER
I.4.Influence des variations de température sur le fonctionnement de l’installation37
CHAP II : Méthode de la thermodynamique en temps fini….40
II.1.Théorie généralisée de la thermodynamique en temps fini .41
II.1.1. Cycle énergétique.…41
II.1.2. Cycle frigorifique….42
II.2.Application de la thermodynamique en temps fini dans la régulation de la centrale de conditionnement d’air..43
II.3.Thermodynamique en temps fini du cycle frigorifique réel à compression mécanique de vapeur : Cas de la centrale à eau glacée de la BEAC-Brazzaville… 51
II.3.1. Aspect technique de la centrale à eau glacée….…..…..53
II.3.2. Optimisation de la centrale à eau glacée…..…..…54
CHAP III : RESULTATS ET ANALYSES59
Résultats60
Analyses…63
Conclusion
LISTE DES TABLEAUX ET FIGURES
LISTE DES FIGURES
Figure 1 : Principe de fonctionnement d’une installation frigorifique…18
Figure 2 : Fonctionnement de l’évaporateur…24
Figure 3 : Graphe de correspondance ∆𝑇0-Humidité relative.26
Figure 4 : Fonctionnement du compresseur…27
Figure 5 : Cycle théorique du compresseur….28
Figure 6 : Fonctionnement du condenseur……30
Figure 7 : Détendeur thermostatique…33
Figure 8 : Diagramme de Mollier…36
Figure 9 : Diagramme T-S…43
Figure 10 : Centrale à eau glacée..…50
Figure 11 : Centrale de traitement d’air…..….50
Figure 12 : Installation frigorifique à compression mécanique des vapeurs.52
Figure 13 : Cycle frigorifique de l’installation..53
LISTE DES TABLEAUX
Tableau 1 : Puissances de destruction de la couche d’ozone et de l’effet de serre..14
Tableau 2: Température d’ébullition de quelques fluides à pression atmosphérique..…19
Tableau 3: Chaleurs sensibles et chaleurs latentes d’évaporation de quelques fluides…..….2
Tableau 4 : Récapitulatif de l’application numérique de l’optimisation de la centrale à eau glacée57
GLOSSAIRE
– Thermodynamique :
C’est une discipline qui étudie des processus des machines, au cours desquels l’énergie est échangée sous forme de chaleur ou de travail mécanique
– Chaleur sensible:
C’est la quantité de chaleur qui provoque la variation de température d’un corps sans modifier son état physique.
– Chaleur latente:
C’est la quantité de chaleur qui provoque le changement d’état d’un corps sans modifier sa température.
– Chaleur latente massique de vaporisation:
C’est la quantité de chaleur qu’il faut fournir à 1 kg d’un corps pour le faire passer de l’état liquide à l’état gazeux sans élever sa température.
– Température critique ou pression critique:
C’est le point d’équilibre (relation pression température) au-dessus duquel on ne peut plus différentier la phase liquide de la phase gazeuse d’un même corps.
Aucune condensation n’est donc possible, le fluide est dit en l’état supercritique.
– La température d’ébullition:
Il s’agit de la température d’ébullition sous pression atmosphérique.
Cette température doit être telle que la pression dans le circuit reste supérieure à la pression atmosphérique, afin d’éviter les entrées d’air.
– Température catastrophique:
C’est la température maximale supportable par un fluide dans un circuit en présence d’huile et de cuivre.
Au-delà de cette température le fluide se décompose et forme des acides fluorhydriques et chlorhydriques.
– Coefficient de performance de Carnot
Le coefficient de performance limite d’un système énergétique fonctionnant dans des conditions de réversibilité.
– Coefficient de performance réel
Le rapport entre l’effet utile désiré et la dépense énergétique.
– Transformation thermodynamique réversible
Transformation qui conserve l’entropie (dénommée également transformation parfaite, idéale).
C’est une transformation inaccessible en pratique puisqu’elle nécessite une évolution selon une succession d’états d’équilibre (transformation quasi-statique), donc elle s’effectue en un temps infini.
– Transformation thermodynamique irréversible
Transformation réelle, entraînant la création d’entropie.
bibliographie-diagramme-enthalpique-MOLLIER
ANNEXES
Centrale à eau glacée
ANNEXE 1
Compresseur
Condenseur
Canalisation à eau glacée
Centre de traitement d’air appelé CTA
Conduit de reprise d’air dans les locaux de la banque
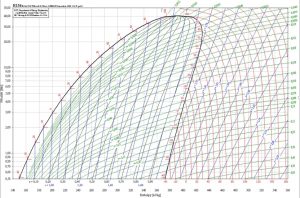
Diagramme de Mollier du fluide frigorigène R134a
ANNEXE 2
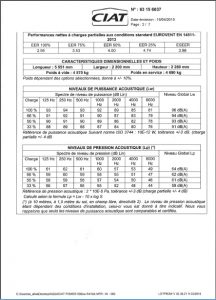
Document technique de la centrale à eau glacée
Procédure de simulation sur MATLAB
* Evolution du coefficient de performance réversible de Carnot
| >> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0429 0.0464 0.0500 0.0571 0.0607 0.0643 0.0679 0.0714 0.0750]; | 0.0536 |
| >>a=x-x; >>b=a+1.1-1; | |
| >> y=1./b; >> plot(x,y); | |
| >>xlabel(‘température adimensionnelle à l’évaporateur’); >>ylabel(‘Coefficient de performance réversible de carnot’); | |
| >>grid |
* Evolution du coefficient de performance irréversible du système réel
| >> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0429 0.0571 0.0607 0.0643 0.0679 0.0714 0.0750] ; | 0.0464 | 0.0500 | 0.0536 |
| >> s=x-0.01497; >> k=x.*x; >> n=k./s; >> m=1-n; >> p=1.1./m; >> t=p-1; >> y=1./t; >> plot(x,y) >> xlabel(‘température adimensionnelle à l’évaporateur’); >> ylabel(‘coefficient de performance irréversible du système réel’); >>grid |
* Evolution du rendement de l’installation
>> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0429 0.0464 0.0500 0.0536
0.0571 0.0607 0.0643 0.0679 0.0714 0.0750] ;
>>s=x-0.01497;
>>k=x.*x;
>> n=k./s;
>> m=1-n;
>> p=1.1./m;
>>t=p-1;
>> y=1./t;
>>a=x-x;
>>b=a+1.1-1;
>> c=1./b;
>> f=y./c;
>> plot(x,f)
>>xlabel(‘Température adimensionnelle à l’évaporateur’);
>>ylabel(‘Le rendement de l’installation par rapport au cycle de Carnot’);
>>grid
* Evolution de la puissance calorifique minimale adimensionnelle
| >> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0429 0.0571 0.0607 0.0643 0.0679 0.0714 0.0750] ; | 0.0464 | 0.0500 | 0.0536 |
| >> a=x./0.01497; >> b=1./x; | |||
| >> c=1./0.01497; >> d=c-b-a; | |||
| >> e=1./d; >> f=0.01497./x; | |||
| >> g=1-f; >> h=1.1.*g; | |||
| >> j=h.*e; >> plot(x,j) | |||
| >>xlabel(‘Température adimensionnelle à l’évaporateur’); >>ylabel(‘Puissance calorifique minimale adimensionnelle’); | |||
| >>grid |
* Evolution du travail mécanique adimensionnel
| >> x=[0.0179 0.0214 0.0250 0.0286 0.0321 0.0357 0.0393 0.0571 0.0607 0.0643 0.0679 0.0714 0.0750] ; | 0.0429 | 0.0464 | 0.0500 | 0.0536 |
| >> a=x./0.01497; | ||||
| >> b=1./x; >> c=1./0.01497; | ||||
| >>d=c-b-a; >> e=1./d; | ||||
| >> f=0.01497./x; >> g=1-f; | ||||
| >> h=1.1.*g; >>j=h.*e; | ||||
| >>k=j-0.0213; >> plot(x,k) | ||||
| >>xlabel(‘Température adimensionnelle à l’évaporateur’); >>ylabel(‘Travail mécanique minimal adimensionnel’); >>grid |
Le travail est divisé en plusieurs pages (articles). Voici la liste :