La méthodologie de flexion électro-magnétique révèle des résultats surprenants sur le comportement des coques à double courbure. En explorant l’impact du potentiel magnétique et de la porosité, cette étude transforme notre compréhension des déformations, avec des implications cruciales pour l’ingénierie moderne.
-
Effet du potentiel magnétique sur la variation de la contrainte de cisaillement xy
-
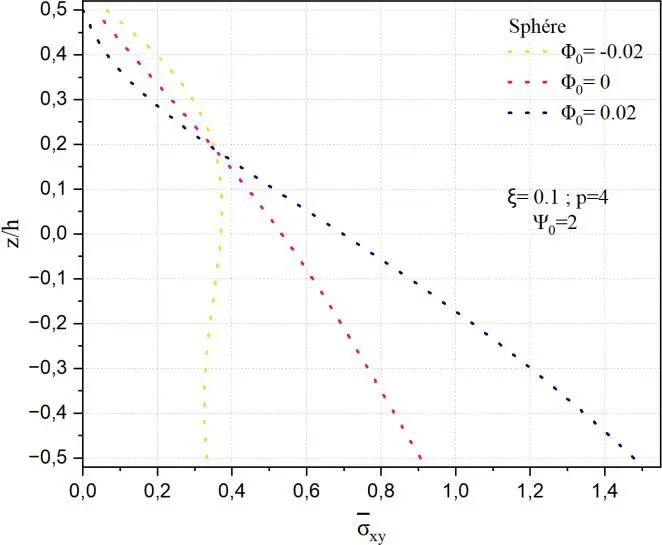Fig. II.26. Variation de la contrainte xy à travers l’épaisseur d’une coque en FGM pour
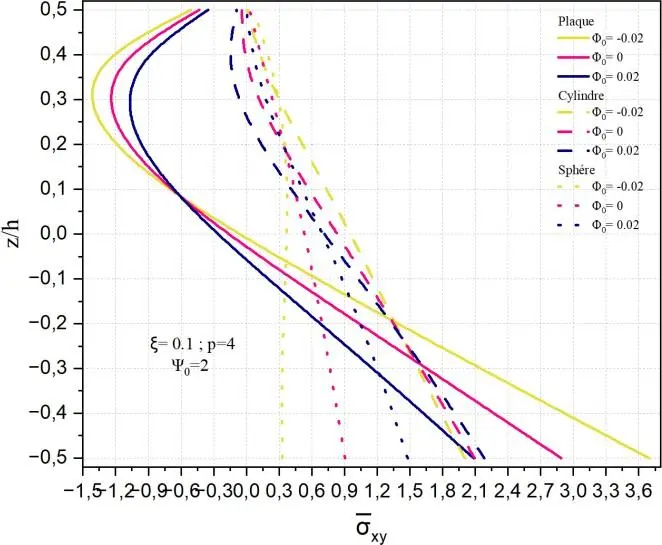
différentes valeurs de potentiel magnétique 0.
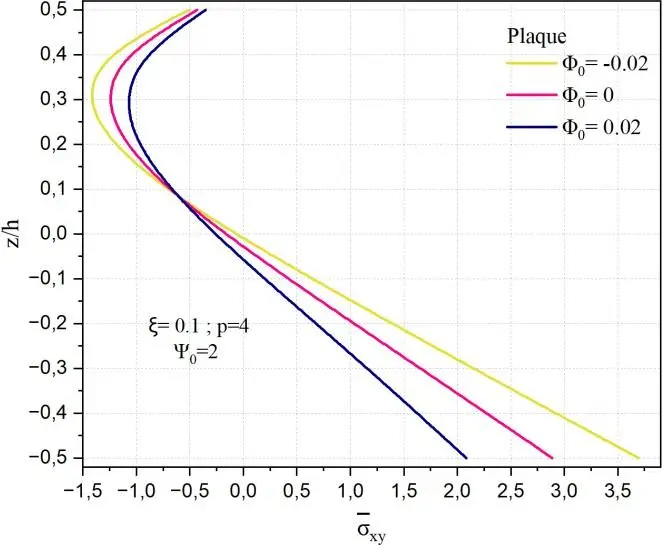
Les Figs. II.26 présentées analysent l’influence du potentiel magnétique 0 sur la distribution de la
contrainte de cisaillement xy en fonction de l’épaisseur normalisée z/h pour trois géométries
(sphère, cylindre, plaque), dans un matériau MEE (magnéto-électro-élastique) avec un potentiel électrique constant 0 2.
Dans un tel matériau couplé multiphysique, l’application conjointe de
champs électrique et magnétique génère des interactions internes complexes entre déformations mécaniques, polarisation électrique et magnétostriction.
L’augmentation du potentiel magnétique 0 (de -0,02 à 0.02) tend à renforcer la réponse mécanique dans toutes les géométries.
Pour la plaque, cette variation induit une augmentation significative de la contrainte de cisaillement xy , surtout vers
les surfaces, avec une accentuation de l’asymétrie du profil à travers l’épaisseur.
Cela s’explique par l’effet magnéto mécanique induit qui amplifie la déformation sous couplage électromagnétique.
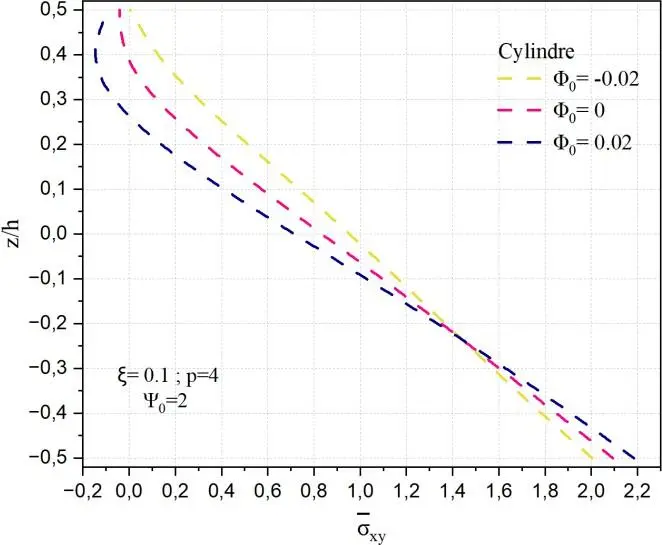
Pour le cylindre et la sphère, les effets sont similaires mais plus modulés par la géométrie : dans la sphère,
la réponse est plus sensible et non linéaire avec une forte croissance de xy pour 0 0.02 , alors que
le cylindre montre une variation plus progressive et linéaire.
Ces résultats mettent en évidence que le champ magnétique appliqué 0, en présence d’un potentiel électrique donné, agit comme un levier
d’activation mécanique supplémentaire, modifiant significativement l’état de contrainte interne selon la configuration géométrique et la position dans l’épaisseur, ce qui est crucial pour le dimensionnement actif de structures MEE dans les dispositifs intelligents, capteurs ou actionneurs.
- Effet du rapport géométrique sue sur la variation de la contrainte normale
xy
- Effet du rapport géométrique sue sur la variation de la contrainte normale
La Fig. II.27 présente la distribution de la contrainte de cisaillement normalisée xy à travers
l’épaisseur d’une plaque FGM soumise à un champ électromagnétique, pour un indice de gradation p=4, une porosité ξ=0,1, un potentiel électrique 0 1 et un potentiel magnétique 0 0.02.
L’effet de la courbure est analysé pour des géométries sphérique et cylindrique, comparées à une plaque plane (R/a = ∞).
Les résultats montrent que l’introduction d’une courbure réduite significativement la contrainte de cisaillement dans le plan xy, en particulier pour les plus faibles rapports R/a.
Cette réduction est plus marquée dans le cas sphérique que cylindrique, traduisant une sensibilité accrue à la double courbure.
La distribution devient également asymétrique à travers l’épaisseur, notamment en raison du gradient de matériau (p = 4) combiné à la porosité, ce qui engendre un déséquilibre des propriétés mécaniques entre les faces supérieure et inférieure.
Ainsi, la courbure géométrique, couplée aux effets multiphysiques et à l’hétérogénéité du matériau, joue un rôle déterminant dans l’intensification et la répartition des contraintes de cisaillement.
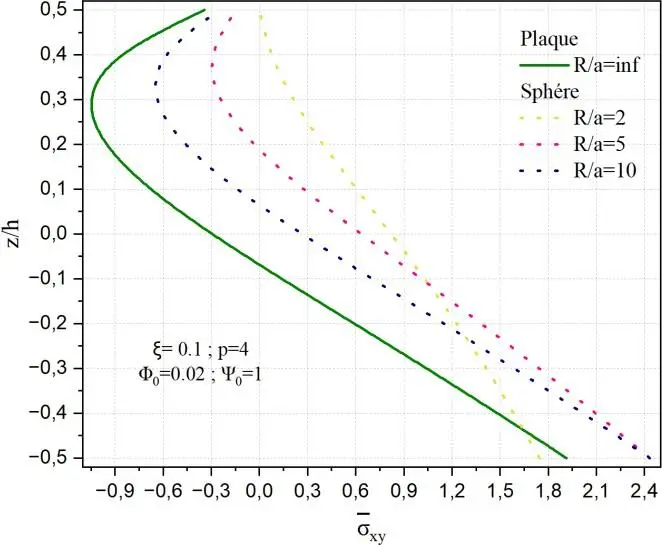
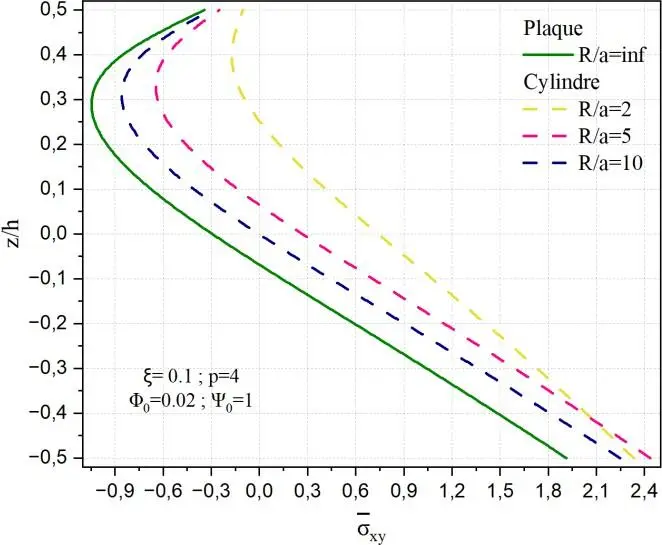
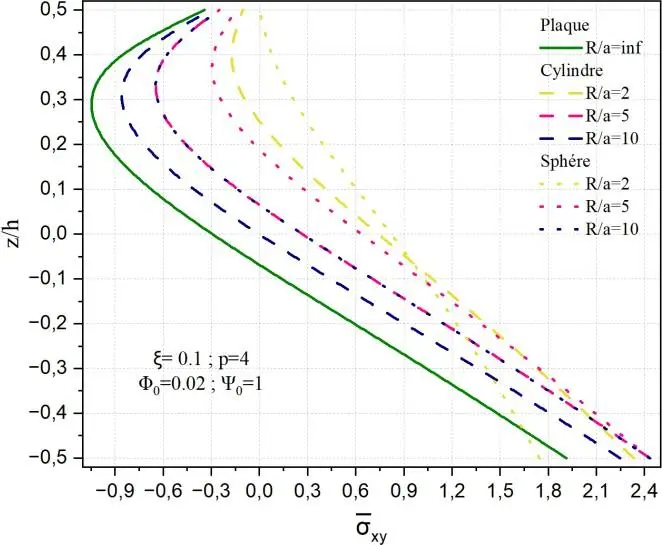
Fig. II.27. Variation de la contrainte xy
à travers l’épaisseur d’une structure en FGM
pour différents rapports R/a.
- Evolution de la déflexion dans les structures sous l’effet la variation du potentiel magnétique 0
Les Figs. II.28 et 29 présentées analysent la comparaison de la déflexion des trois structures sous
l’effet la variation du potentiel magnétique 0
en présence de potentiel électrique constant
0 2,0,2.
Il est à noter que la variation du potentiel magnétique conduit à une variation très importance de la déflexion de la plaque en comparaison avec les autres structures.
Lorsque le potentiel magnétique et positif conduit à un déplacement positif est vice versa.
Un comportement inverse se produit pour les structures cylindre et sphère.
Il est à remarquer que le matériau FGM possédant l’indice de puissance important (p=4) produit une déflexion moins importante
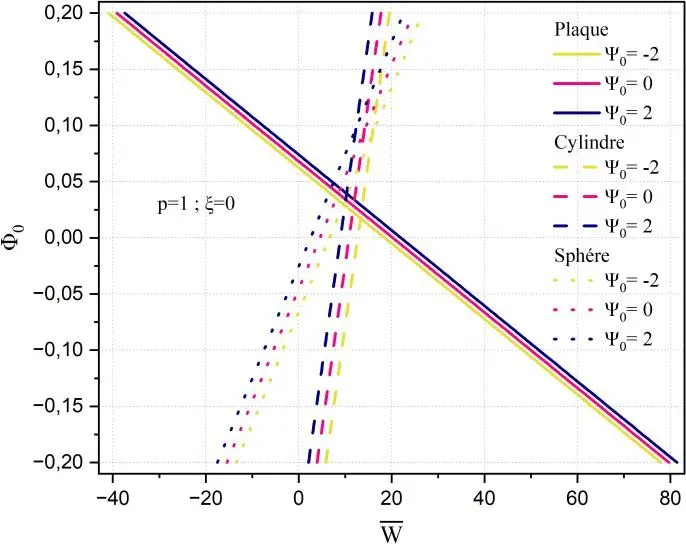
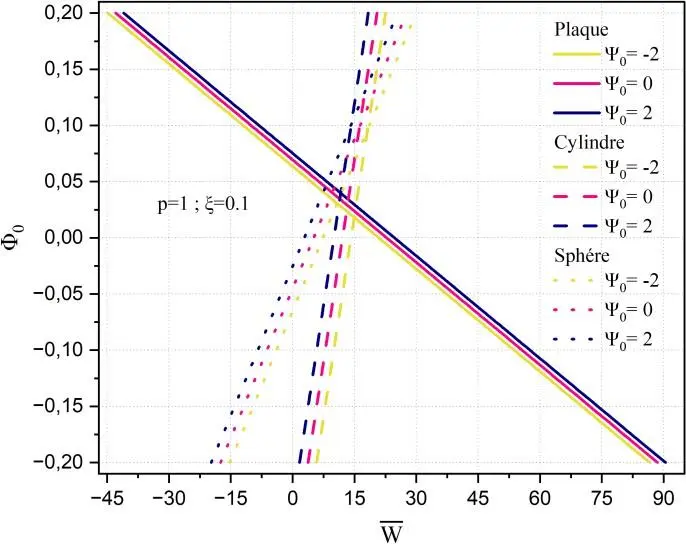
Fig. II.28. Déflexion centrale adimensionnelle de la coque FGM (p=1) en fonction des différents
paramètres a) Effet de 0 sur la déflexion 0 , b) Effet de 0 sur la déflexion 0.1
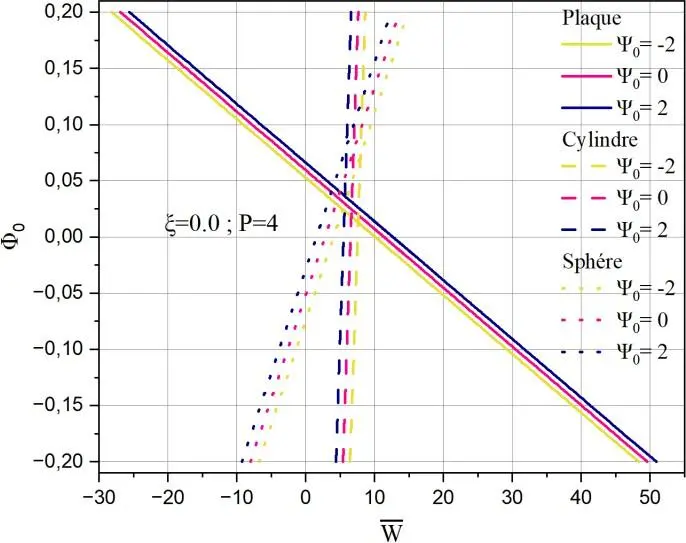
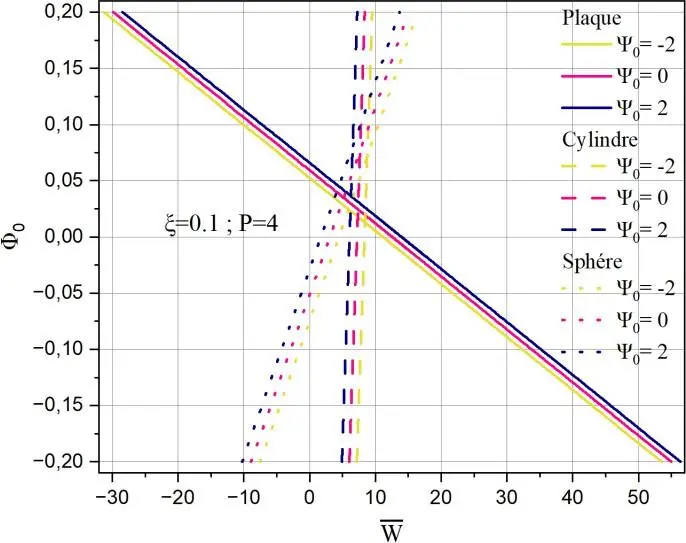
Fig. II.29. Déflexion centrale adimensionnelle de la coque FGM (p=4) en fonction des différents
paramètres a) Effet de 0 sur la déflexion 0 , b) Effet de 0 sur la déflexion 0.1
Introduction générale
68
Conclusion générale et perspectives
Notre modeste étude a permis de mettre en évidence la complexité du comportement mécanique des structures poreuses en matériaux à gradient fonctionnel (FGM) soumises à des champs électromagnétiques.
Il ressort que la réponse des contraintes normales et de cisaillement est le fruit d’interactions synergiques entre plusieurs facteurs : la porosité, la courbure géométrique, le gradient fonctionnel de matériau, ainsi que les potentiels électrique et magnétique appliqués.
Le potentiel électrique, par effet piézoélectrique, induit des déformations importantes, notamment dans les couches supérieures des structures, avec des déplacements amplifiés dans les zones éloignées du plan neutre.
En parallèle, le potentiel magnétique exerce un effet tout aussi déterminant : il modifie la répartition des contraintes normales et transverses en fonction de son intensité et de sa polarité.
En particulier, un potentiel magnétique négatif tend à intensifier les contraintes en compression, tandis qu’un potentiel positif les atténue.
Ces effets sont fortement dépendants de la géométrie : les coques sphériques et cylindriques, du fait de leur courbure, présentent une sensibilité accrue au champ magnétique, traduite par des redistributions asymétriques des efforts internes.
La porosité contribue à l’assouplissement local du matériau, entraînant une augmentation des déflexions et une amplification des contraintes maximales, en particulier dans les couches céramiques.
Cependant, son impact est fortement modulé par la géométrie : il est modeste dans les coques sphériques, mais devient critique dans les plaques planes.
La géométrie structurelle joue un rôle prépondérant dans la distribution des contraintes.
Les coques sphériques, du fait de leur double courbure, génèrent un effet de confinement renforcé, stabilisant la réponse mécanique et atténuant l’influence des défauts tels que la porosité.
En revanche, les plaques montrent une plus grande vulnérabilité aux hétérogénéités de matériau et aux effets électromagnétiques.
Enfin, le matériau FGM influence localement la rigidité et les transferts d’efforts à travers l’épaisseur.
Les effets combinés de la porosité, des champs électromagnétiques et de la courbure ne peuvent être saisis correctement qu’en recourant à des théories de cisaillement d’ordre élevé (HSDT), particulièrement adaptées aux configurations multiphysiques complexes.
En conclusion, cette étude démontre que l’optimisation des structures FGM poreuses nécessite une intégration conjointe des effets du potentiel magnétique, du potentiel électrique, de la porosité, de la courbure géométrique et du profil fonctionnel du matériau.
Ces paramètres constituent des leviers essentiels pour la conception de structures intelligentes et adaptatives capables d’évoluer efficacement dans des environnements soumis à des sollicitations multiphysiques intenses.
En somme, cette étude souligne que l’optimisation de la réponse mécanique des structures FGM poreuses repose sur une approche multiparamétrique intégrant les effets conjoints des champs
électromagnétiques, de la porosité, de la géométrie et des gradients de matériau.
Ces résultats fournissent des éléments fondamentaux pour la conception rationnelle de structures intelligentes, adaptatives et performantes, destinées à fonctionner dans des environnements physiques complexes et contraignants.
Notre étude ouvre des perspectives prometteuses et pourra être poursuivie par d’autres étudiants.
Nous pouvons citer comme perspectives l’exploration approfondie des effets non linéaires des champs électromagnétiques, l’étude des comportements dynamiques sous sollicitations variables, ainsi que l’intégration de modèles plus complexes de porosité et d’hétérogénéité dans les matériaux à gradient fonctionnel poreux.
Extension aux analyses dynamiques et vibrations couplées
Les travaux futurs pourraient intégrer des analyses dynamiques des structures FGM poreuses sous champs électromagnétiques variables dans le temps.
Étudier les effets combinés des vibrations mécaniques et des champs électromagnétiques dynamiques permettrait de mieux comprendre la stabilité et la durabilité des structures dans des environnements réels, tels que les applications aérospatiales ou biomédicales.
Questions Fréquemment Posées
Quel est l’effet du potentiel magnétique sur la contrainte de cisaillement dans les coques à double courbure?
L’augmentation du potentiel magnétique tend à renforcer la réponse mécanique dans toutes les géométries, induisant une augmentation significative de la contrainte de cisaillement, surtout vers les surfaces.
Comment la courbure géométrique influence-t-elle la contrainte de cisaillement dans les structures FGM?
L’introduction d’une courbure réduit significativement la contrainte de cisaillement dans le plan xy, en particulier pour les plus faibles rapports R/a, et la distribution devient asymétrique à travers l’épaisseur.
Quelle est l’importance de la variation du potentiel magnétique sur la déflexion des structures?
La variation du potentiel magnétique conduit à une variation très importante de la déflexion de la plaque en comparaison avec les autres structures, avec un comportement inverse selon que le potentiel est positif ou négatif.