Comment surmonter les défis de la déformation des coques à double courbure ?

La déformation des coques à double courbure révèle des résultats surprenants : une étude récente démontre que le potentiel électrique influence significativement la contrainte de cisaillement. Ces découvertes ouvrent la voie à de nouvelles applications dans le domaine des matériaux composites, transformant notre compréhension des structures flexibles.

• 1. Effet du potentiel électrique sur la variation de la contrainte de cisaillement  _xz

Les Figs.II.17 illustrent l’influence du paramètre  ₀ sur la distribution de la contrainte de

cisaillement transverse normalisée  _xz à travers l’épaisseur réduite z/h pour trois types de structures

: une plaque, un cylindre et une sphère. Les autres paramètres, à savoir ξ=0.1, p=4 et ₀ = 0.02, sont maintenus constants afin d’isoler l’effet de  ₀, qui semble représenter un champ transversal ou un

gradient de matériau. On observe que l’impact de  ₀ dépend fortement de la géométrie de la structure.

Dans le cas de la plaque, la distribution de  _xz reste symétrique, mais son intensité varie

significativement selon la valeur de  ₀. Une augmentation de  ₀ engendre une augmentation de la

contrainte transverse maximale, traduisant une concentration accrue des efforts de cisaillement. Ainsi,

la plaque avec  ₀ = 2 présente des contraintes bien plus élevées que celle avec  ₀ = -2, suggérant

que le paramètre  ₀ joue un rôle similaire à un renforcement ou à un affaiblissement du cisaillement

effectif à travers l’épaisseur. Ce comportement est cohérent avec une variation des propriétés mécaniques en direction transverse.

Pour le cylindre, bien que la tendance reste similaire à celle de la plaque (augmentation de  _xz avec

 ₀), l’effet est nettement plus modéré. Les courbes correspondant aux différentes valeurs de  ₀ sont

très proches, ce qui indique que la courbure moyenne du cylindre agit comme un facteur stabilisant, amortissant l’effet de ce paramètre. La répartition des contraintes y est plus uniforme, ce qui reflète une certaine robustesse géométrique vis-à-vis des variations de propriétés à travers l’épaisseur.

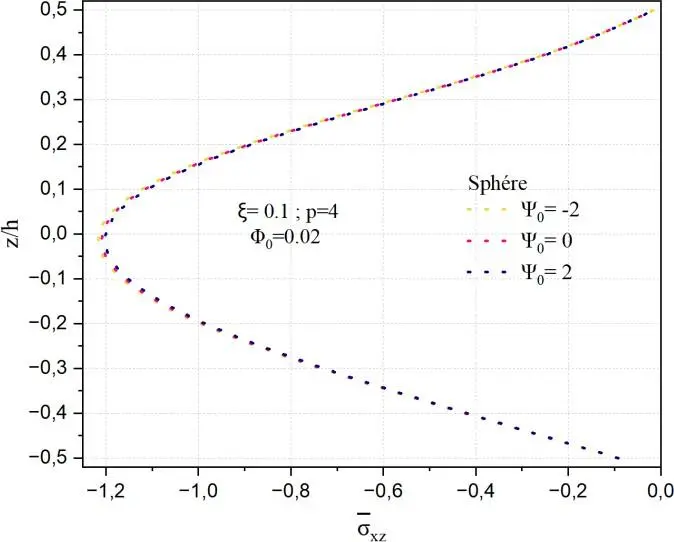
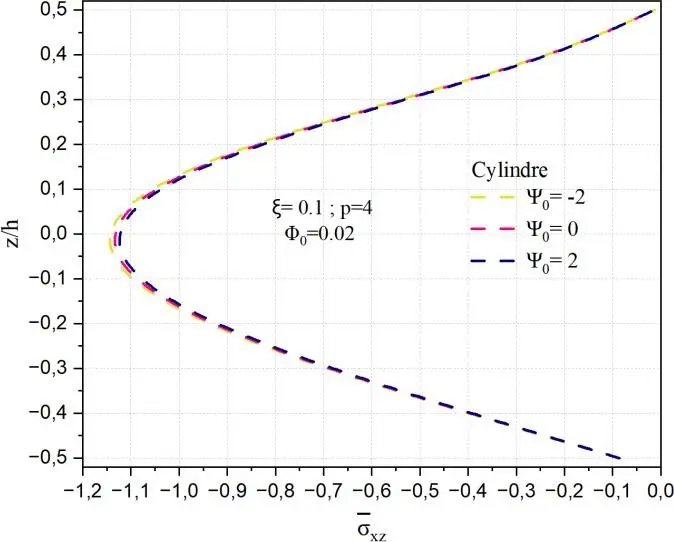
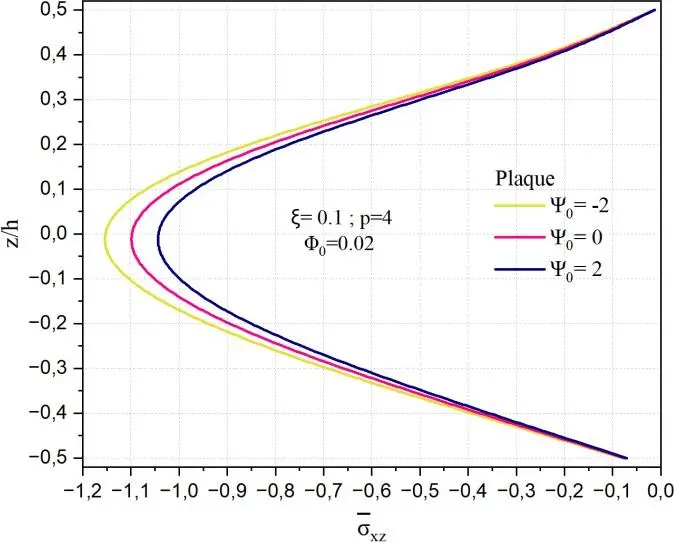
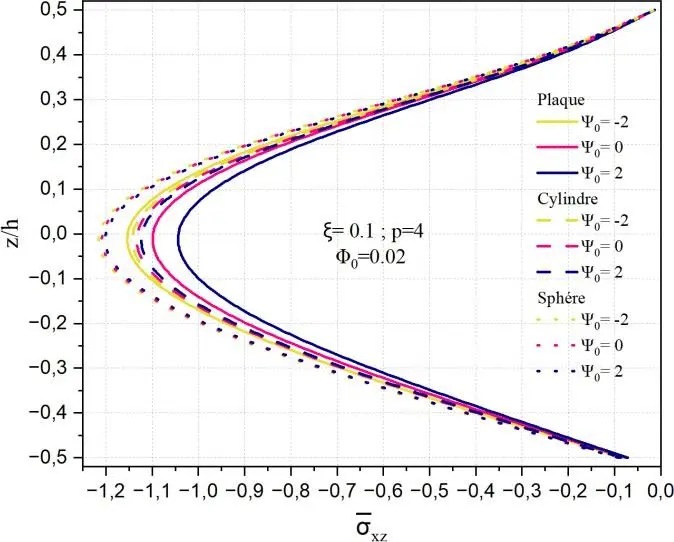
Fig. II.17. Variation de la contrainte de cisaillement transverse  xz à travers l’épaisseur de la

coque en FGM pour différentes valeurs de potentiel électrique  0.

En revanche, dans le cas de la sphère, la courbure double intensifie nettement l’effet de  ₀. On observe une forte asymétrie dans la distribution de la contrainte de cisaillement, surtout pour  ₀ = 2

, où les contraintes sont nettement concentrées vers la face inférieure de la structure. Cette réponse traduit une interaction complexe entre la géométrie fortement courbée et les effets induits par  ₀,

avec une amplification locale du cisaillement transverse. Ainsi, la sphère est beaucoup plus sensible aux effets de gradient transverse que les autres configurations.

L’effet de  ₀ sur la contrainte transverse  _xz dépend fortement de la géométrie : il est marqué dans

les plaques, atténué dans les cylindres et fortement amplifié dans les sphères. Ces résultats soulignent l’importance de prendre en compte à la fois les propriétés de variation du matériau et la géométrie de la structure pour prédire fidèlement les réponses mécaniques internes, notamment dans les structures courbes fonctionnellement graduées.

• 1. Effet du potentiel magnétique sur la variation de la contrainte de cisaillement  _xz

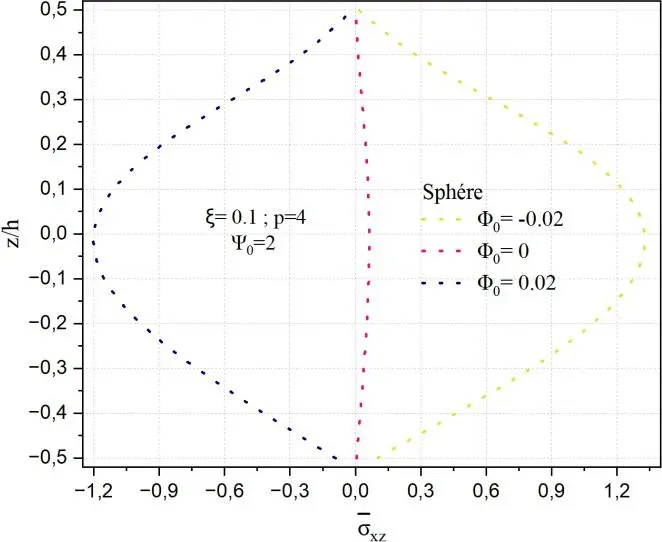
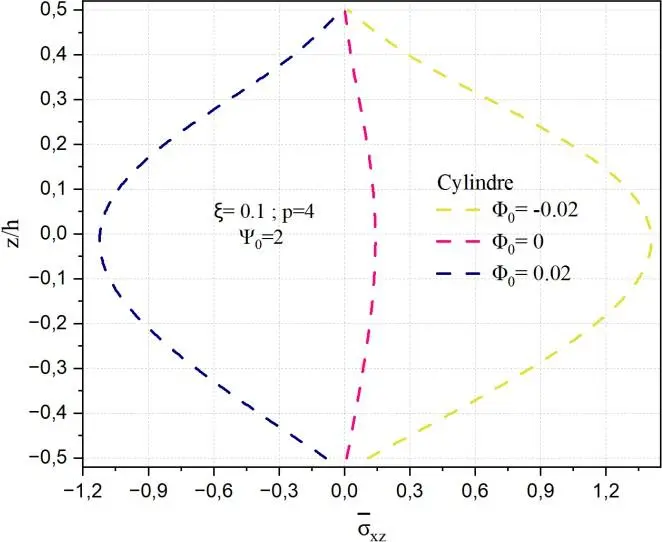
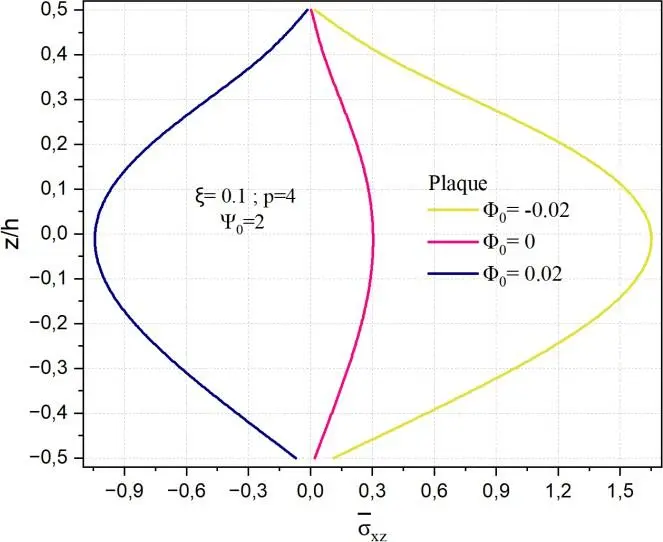
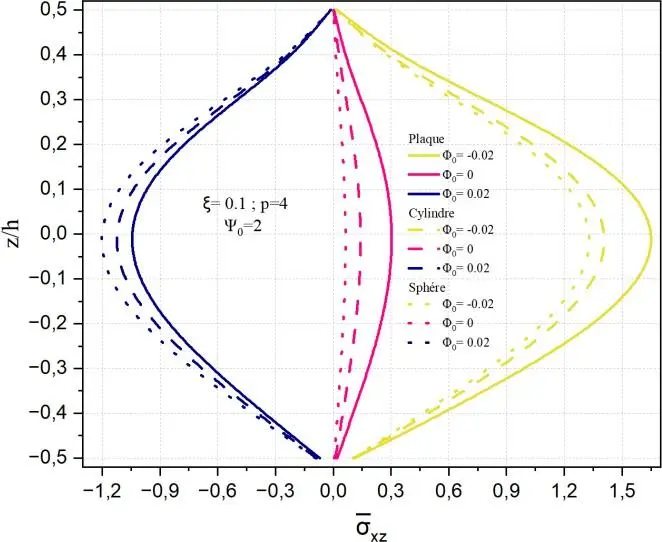
Fig. II.18. Variation de la contrainte de cisaillement transverse  xz à travers l’épaisseur de la

coque en FGM pour différentes valeurs de potentiel magnétique 0.

Les Figs.II.18 fournies illustrent la distribution de la contrainte de cisaillement transverse normalisée

 _xz selon l’épaisseur réduite z/h, pour trois géométries structurelles distinctes — plaque, cylindre et

sphère — en fonction du paramètre de porosité initiale ₀, avec des valeurs fixées de ξ=0.1, p=4 et

₀ = -0.02,0,0.02. L’objectif est de mettre en évidence l’influence de la porosité et du potentiel magnétique du matériau fonctionnellement gradué (FGM) sur la réponse en cisaillement transverse dans des configurations géométriques variées.

Pour la plaque, la courbe de  _xz est fortement influencée par la valeur ₀. Un potentiel magnétique

négatif ₀ = -0.02 induit une augmentation significative de la contrainte transverse maximale,

atteignant des valeurs supérieures à 1,5, ce qui traduit une élévation notable de la rigidité effective en cisaillement dans la zone centrale de la plaque. À l’inverse, un potentiel magnétique positif ( ₀ = 0.02

) réduit considérablement cette contrainte, suggérant un matériau plus souple ou endommagé dans les zones critiques. La forme symétrique et convexe des courbes indique que le cisaillement est maximal au centre de la plaque et tend vers zéro aux interfaces, conformément au comportement attendu d’un champ de cisaillement transverse sous flexion pure dans des structures symétriques.

La réponse du cylindre suit une tendance similaire à celle observée dans la plaque, mais avec des

intensités légèrement moindres. La variation de ₀ influe encore sensiblement sur l’amplitude

maximale de  _xz bien que l’effet soit atténué par la courbure unidirectionnelle du cylindre. La

géométrie cylindrique engendre une répartition plus douce de la contrainte, avec des courbes légèrement moins pentues près des interfaces. Néanmoins, la symétrie reste globalement respectée, indiquant que l’effet de la porosité agit principalement sur l’amplitude du cisaillement plutôt que sur sa distribution géométrique.

Le cas de la sphère présente un comportement plus complexe. Bien que l’effet de ₀ soit toujours manifeste, les courbes sont davantage étalées et moins abruptes, suggérant une atténuation plus marquée du cisaillement vers les faces supérieure et inférieure. La double courbure de la sphère

semble amortir l’effet direct de la porosité sur la distribution du cisaillement. Néanmoins, les valeurs

extrêmes de  _xz restent fortement influencées : une porosité positive génère une augmentation

prononcée de la contrainte transverse, tandis qu’une porosité négative en réduit considérablement l’intensité. Cette réponse souligne l’interaction complexe entre les propriétés de matériau (via ₀) et la géométrie intrinsèque dans le contrôle du comportement mécanique.

Les résultats confirment que le paramètre de porosité initiale ₀ joue un rôle critique dans la

modulation des contraintes de cisaillement transverse dans les structures FGM. Plus spécifiquement, une porosité positive accroît notablement la rigidité apparente, augmentant les contraintes internes, tandis qu’une porosité négative les atténue. Par ailleurs, la géométrie influence fortement la manière dont ces effets se manifestent : les plaques sont les plus sensibles à ₀, suivies des cylindres, puis des

sphères, qui présentent une réponse plus régularisée. Ces observations sont essentielles pour la conception optimisée de structures FGM, notamment en ce qui concerne la distribution de la porosité dans les applications où les contraintes de cisaillement sont prépondérantes.

• 1. Effet du rapport géométrique sur la variation de la contrainte normale  _xz

La Fig.II.19 montre l’influence du rapport géométrique R/a sur la distribution de la contrainte

cisaillement  xz selon l’épaisseur normalisée z/h pour des coques FGM poreuses soumises à un

potentiel électrique constant  ₀ = 1 et un couplage magnétique ₀ = 0.02. La comparaison des

résultats entre une plaque (R/a=∞) et des coques sphériques de différents rayons de courbure (rapport R/a=2,5,10), tandis que le graphe de gauche montre le cas équivalent pour des coques sphériques. On observe que la courbure a un effet significatif sur l’amplitude et la répartition des contraintes. Au fur et à mesure que le rapport R/a décroit, la contrainte maximale en compression croit, atteignant environ

-1 pour la plaque et -1.2, -1.1 lorsque R/a=2 dans les deux géométries respectivement sphère et cylindre. Cette accentuation est plus marquée dans les coques sphériques que cylindriques pour les petits rapports R/a, ce qui s’explique par une double courbure dans le cas sphérique, induisant un effet de confinement plus important.

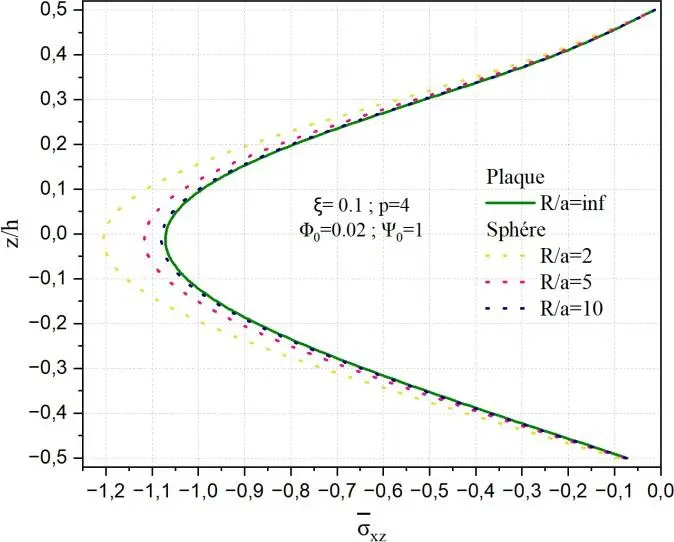
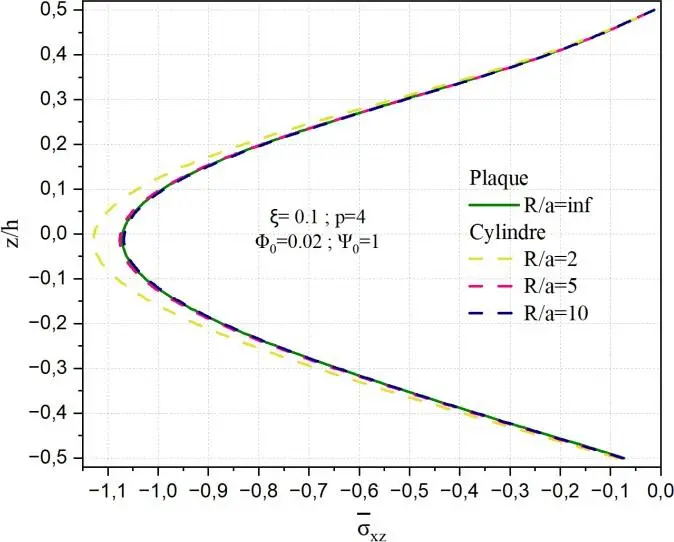
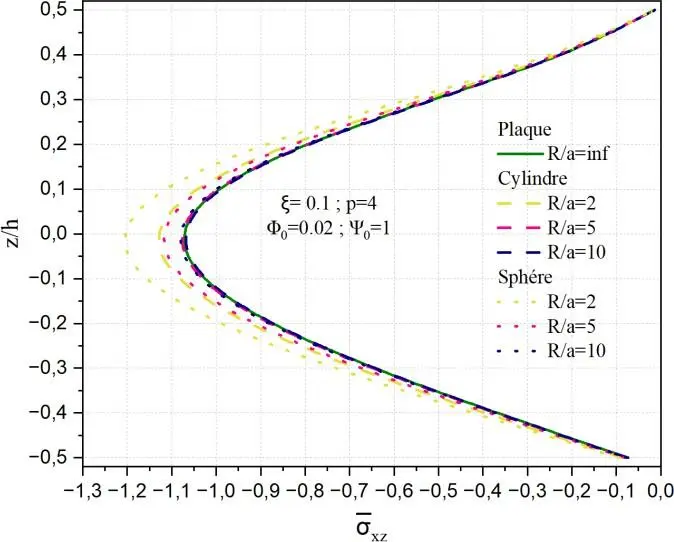
Fig. II.19. Variation de la contrainte de cisaillement transverse  xz à travers l’épaisseur de

la coque en FGM pour différents rapports géométriques R/a.

• 1. Effet de la porosité sur la variation de la contrainte de cisaillement  yz

Dans ce cas, le comportement est similaire à celui du cas de la Fig.II.16.

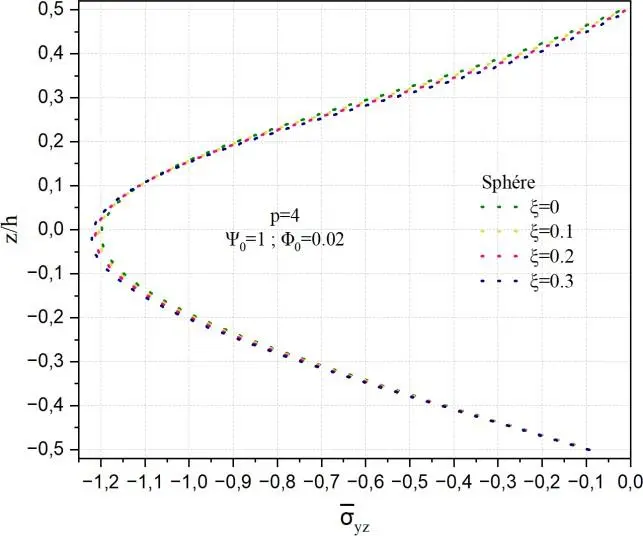
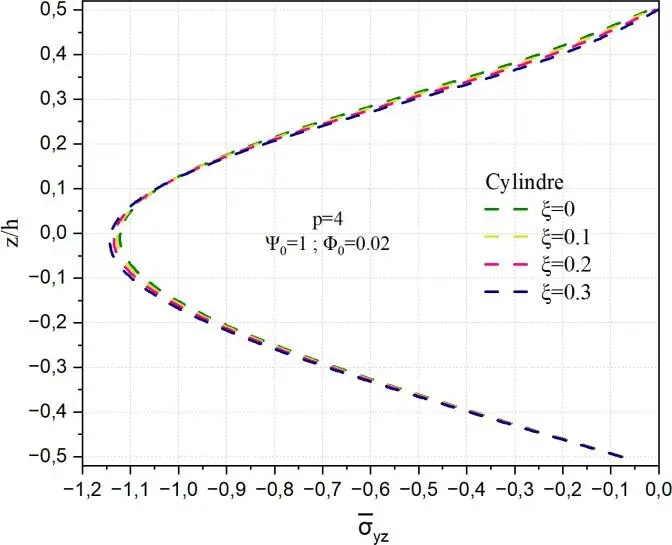
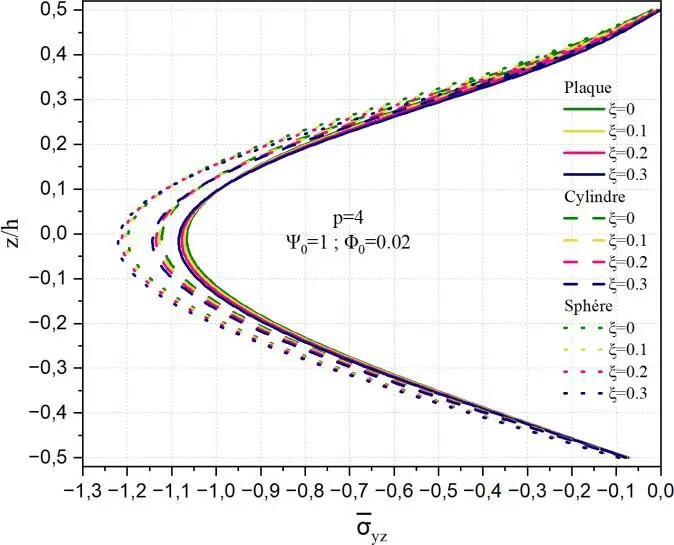
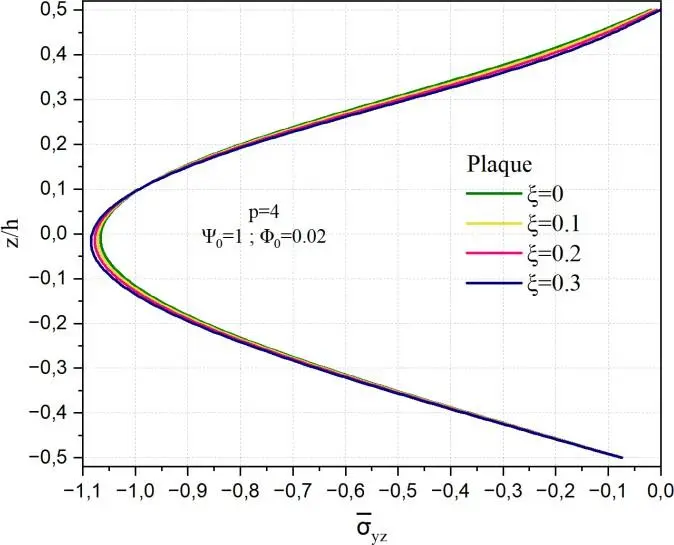
Fig. II.20. Variation de la contrainte de cisaillement transverse  _yz à travers l’épaisseur de la coque

en FGM pour différentes valeurs de porosité ().

• 1. Effet du potentiel électrique sur la variation de la contrainte de cisaillement  yz

La Fig.II.21 représente la distribution de la contrainte de cisaillement transverse normalisée  yz à

travers l’épaisseur normalisée z/h, pour différentes géométries (sphère, cylindre, plaque plane) en fonction du potentiel électrique  ₀, avec un matériau FGM caractérisé par un indice de gradation p=4, une porosité ξ=0,1 et un potentiel magnétique fixé à ₀ = 0.02.

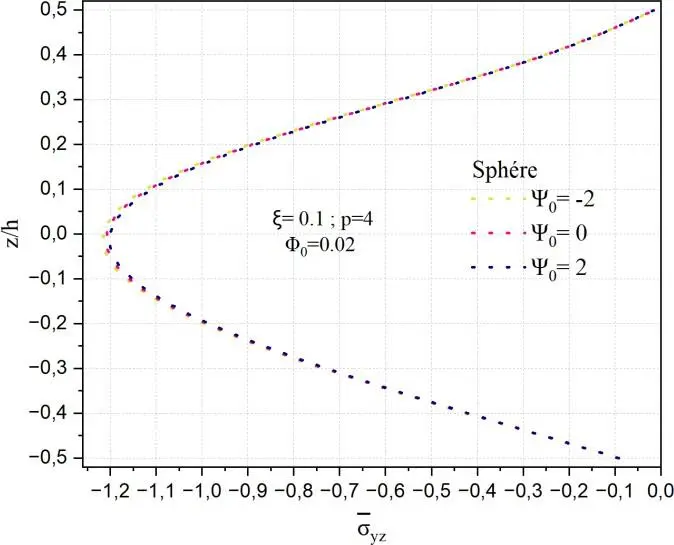
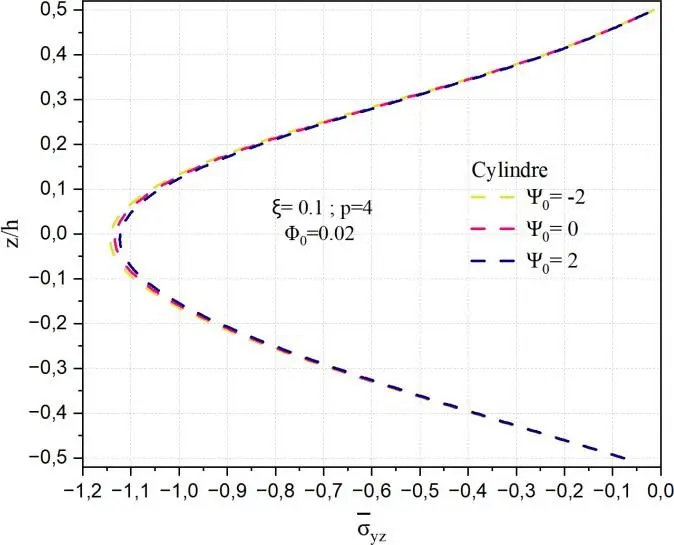
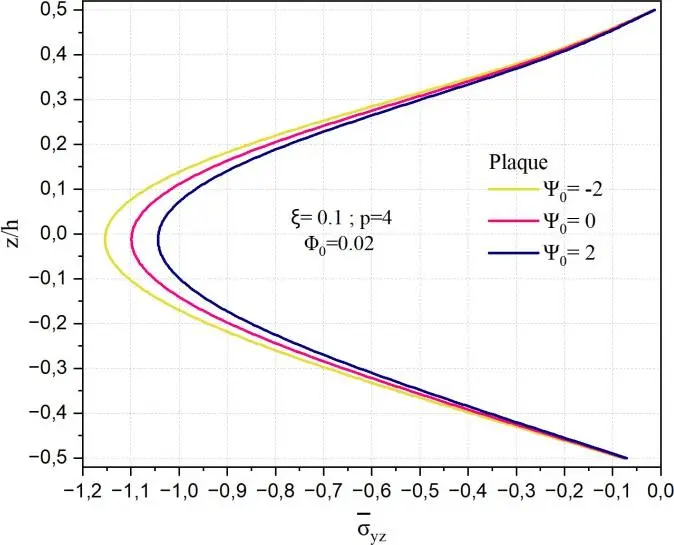
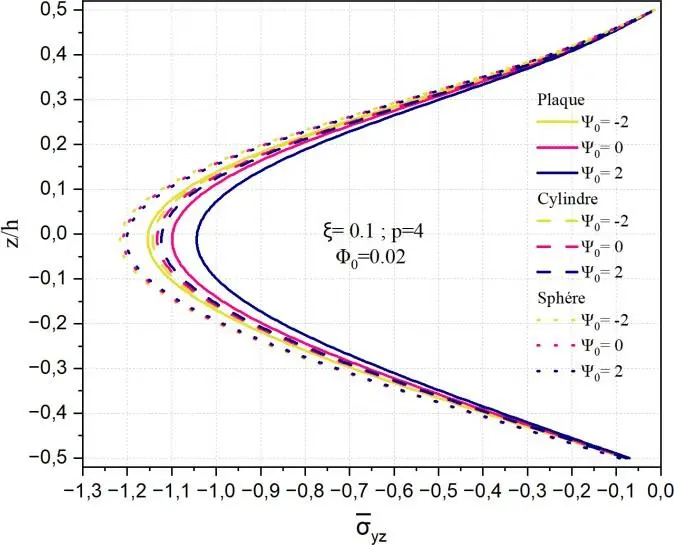
Fig. II.21. Variation de la contrainte de cisaillement transverse  _yz

à travers l’épaisseur d’une

coque en FGM pour différentes valeurs de potentiel électrique 𝜓₀.

Dans les trois sous-figures, on observe que la contrainte  yz

est strictement négative à travers

l’épaisseur, avec un profil globalement symétrique, dont l’intensité maximale est centrée autour du

plan médian (z/h=0). L’influence du potentiel électrique  ₀

est clairement visible : lorsqu’il

augmente de -2 à 2, la contrainte devient progressivement plus intense (en valeur absolue), indiquant une forte sensibilité du cisaillement transverse à l’effet électromécanique. Dans le cas de la géométrie sphérique, cette sensibilité est très marquée : les courbes montrent une variation significative de  yz

entre les cas  ₀ = -2,0,2.

L’effet de  ₀

semble amplifier ou atténuer le profil selon son signe,

modifiant de manière notable l’amplitude du cisaillement.

Questions Fréquemment Posées

Quel est l’effet du potentiel électrique sur la contrainte de cisaillement dans les coques à double courbure?

L’augmentation du potentiel électrique  0 engendre une augmentation de la contrainte transverse maximale, traduisant une concentration accrue des efforts de cisaillement, avec un impact qui dépend fortement de la géométrie de la structure.

Comment la géométrie influence-t-elle la réponse des coques à double courbure aux potentiels électriques?

La réponse dépend de la géométrie : elle est marquée dans les plaques, atténuée dans les cylindres et fortement amplifiée dans les sphères, soulignant l’importance de la géométrie dans la prédiction des réponses mécaniques internes.

Quel est l’impact du potentiel magnétique sur la contrainte de cisaillement dans les coques à double courbure?

Un potentiel magnétique négatif 0 = -0.02 induit une augmentation significative de la contrainte transverse maximale dans les plaques, mettant en évidence l’influence de la porosité et du potentiel magnétique sur la réponse en cisaillement transverse.