Quelles sont les perspectives futures de la flexion électromagnétique ?

Les perspectives futures en flexion électromagnétique révèlent des interactions inattendues entre la porosité et les champs électriques et magnétiques. Cette étude novatrice promet de transformer notre compréhension des coques à double courbure, avec des implications cruciales pour l’ingénierie des matériaux avancés.

• 1. Effet du potentiel magnétique sur la variation de la contrainte  _z

La Fig. II.14 illustre la distribution de la contrainte normale transverse à travers l’épaisseur d’une coque poreuse en matériau à gradient fonctionnel (FGM), pour différentes valeurs du potentiel magnétique ₀, un indice de puissance de la distribution des propriétés matériaux p=4, et en présence d’un champ électrique  ₀  2. La porosité intrinsèque du matériau est également prise en compte dans l’analyse,   0.1.

Il est à observer que les contraintes normales minimales se localisent dans la couche en céramique de la plaque, avec une valeur avoisinant -2.1, tandis que les contraintes maximales, de l’ordre de 0.90 apparaissent dans la région supérieure de la coque (environ à z/h=0,25) lorsque le potentiel magnétique est positif ₀  0.02. La contrainte en compression s’avère environ deux fois plus importante que celle en traction, cette dernière étant plus marquée dans les autres configurations structurelles.

Par ailleurs, la diminution du champ potentiel magnétique, allant d’une valeur négative à une valeur positive, induit une réduction significative de la contrainte maximale : elle diminue d’environ 84 % dans le cas de la géométrie sphérique et de 50 % dans le cas cylindrique. Ce comportement met en évidence l’influence notable du champ magnétique sur la réponse mécanique de la coque FGM poreuse.

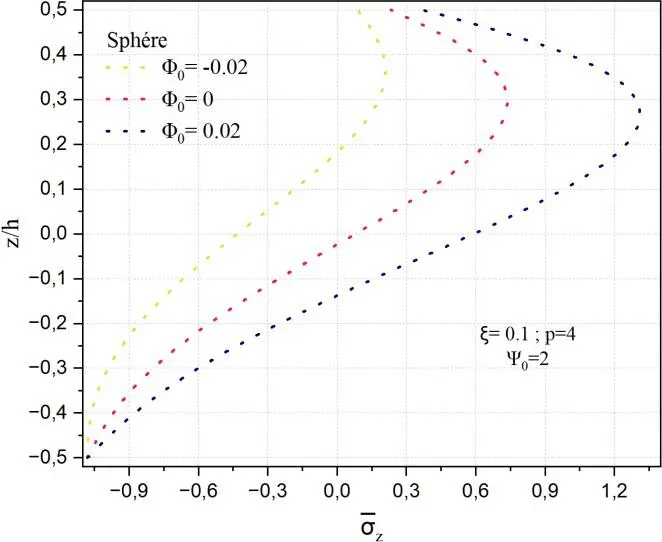
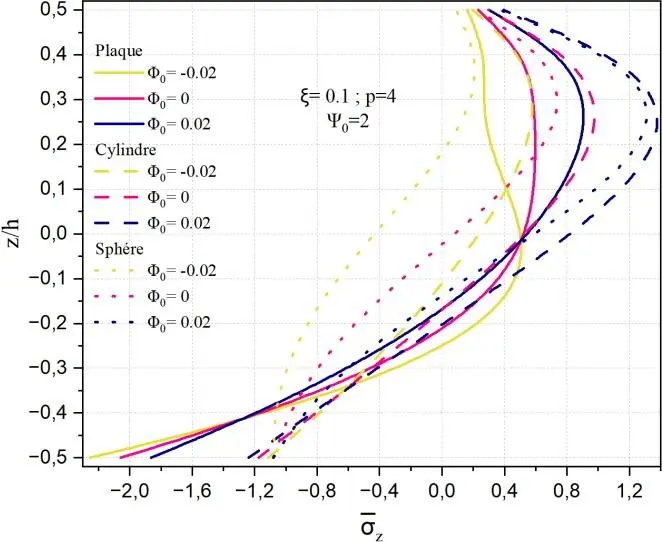
Fig. II.14. Variation de la contrainte normale z à travers l’épaisseur de la coque en FGM pour

différentes valeurs de potentiel magnétique 0.

• 1. Effet du rapport géométrique sur la variation de la contrainte  _z

La Fig.II.15 présente l’influence du rapport géométrique R/a sur la distribution de la contrainte normale transverse  _z selon l’épaisseur normalisée z/h, pour des coques poreuses en matériau à gradient fonctionnel (FGM) soumises à un potentiel électrique constant  ₀  1 et à un couplage magnétique ₀  0.02. La comparaison est effectuée entre une plaque (R/a→∞) et des coques sphériques de différents rayons de courbure (R/a=2, 5, 10), tandis que le graphe de gauche illustre les résultats pour des coques cylindriques soumises aux mêmes conditions.

Les résultats montrent que la courbure influence de manière significative l’amplitude et la répartition de la contrainte normale. Plus précisément, à mesure que le rapport R/a décroit, la contrainte maximale en compression devient plus importante. Par exemple, on observe une valeur de σz≈-1.2 pour la plaque, contre environ 1.2 pour la coque sphérique et la coque cylindrique lorsque R/a=2.

Cette accentuation de la contrainte est plus marquée dans le cas des coques sphériques, en raison de leur double courbure, qui induit un effet de confinement plus prononcé par rapport aux coques cylindriques, à courbure simple. À l’inverse, lorsque R/a augmente, les profils de contraintes convergent vers celui d’une structure plane, avec une augmentation notable de la contrainte maximale localisée dans la couche céramique du FGM. Dans l’ensemble, les distributions de  _z restent asymétriques à travers l’épaisseur, ce qui reflète l’influence conjointe de la porosité, de l’hétérogénéité fonctionnelle du et de la géométrie de la coque.

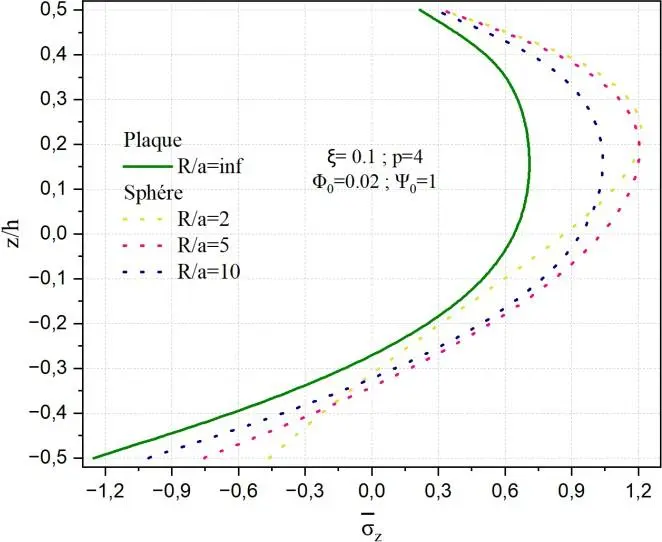
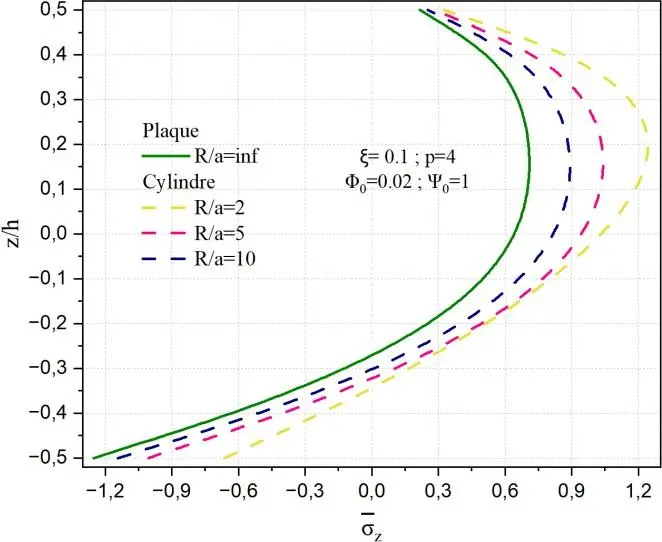
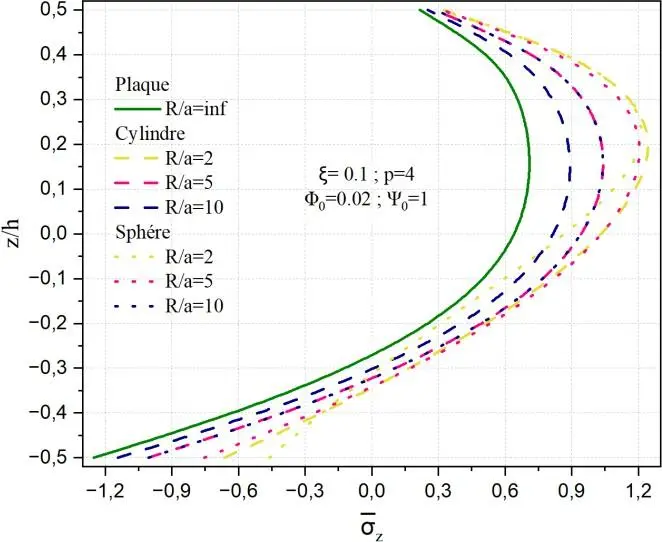
Fig.II.15. Variation de la contrainte normale  z

à travers l’épaisseur de la coque en FGM pour

différents rapports géométriques R/a.

• 1. Effet de la porosité sur l’évolution de la contrainte transverse  _xz

dans les structures

La Fig. II.16 présente la variation de la contrainte de cisaillement transverse normalisée  _xz à travers l’épaisseur réduite z/h pour trois géométries différentes : une plaque, un cylindre et une sphère, en considérant plusieurs valeurs du paramètre de porosité ξ, qui représente vraisemblablement un facteur d’hétérogénéité du matériau. Dans le cas de la plaque, la distribution de  _xz est quasi parabolique et symétrique par rapport au plan médian, avec une valeur maximale au centre (z/h=0) et nulle aux faces libres, ce qui correspond au comportement classique d’une plaque en flexion selon les théories de type Reissner-Mindlin ou HSDT. L’augmentation du paramètre ξ entraîne une légère augmentation de la contrainte de cisaillement en valeur absolue, traduisant une modification de la rigidité effective au cisaillement due à la variation de la fraction volumique du matériau.

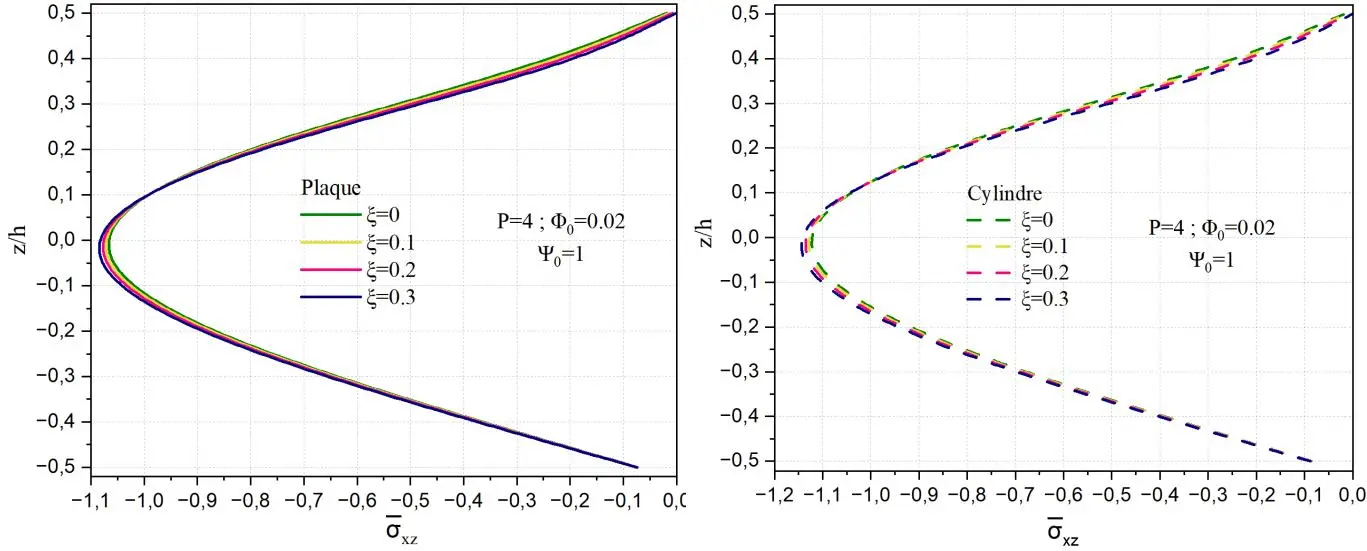
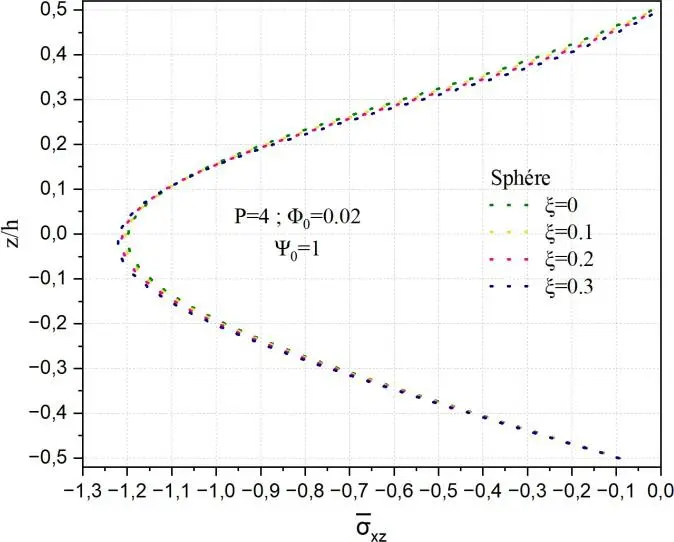
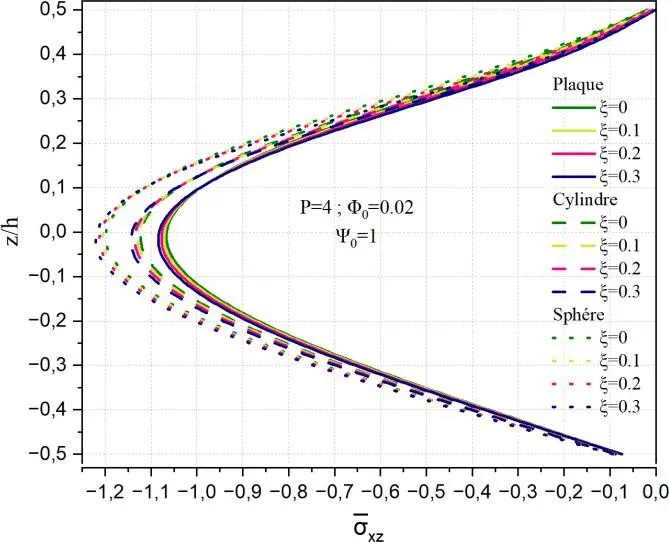
Fig. II.16. Variation de la contrainte de cisaillement transverse  xz à travers l’épaisseur d’une coque

en FGM pour différentes valeurs de porosité ( ).

Dans le cas du cylindre, la distribution de  _xz reste similaire à celle de la plaque mais devient légèrement asymétrique, ce qui reflète l’influence de la courbure moyenne constante de la coque cylindrique. Le profil conserve néanmoins sa forme globale, avec un maximum au centre. L’augmentation de ξ a un effet comparable à celui observé pour la plaque, avec une augmentation modérée de la contrainte transverse. En revanche, pour la coque sphérique, la distribution de  _xz devient fortement asymétrique. Le maximum ne se situe plus au centre de l’épaisseur, et la forme du profil est significativement influencée par la double courbure. L’effet du paramètre ξ y est également plus marqué, indiquant que la combinaison entre la géométrie sphérique et l’hétérogénéité du matériau engendre une redistribution plus complexe des contraintes de cisaillement.

Ainsi, cette étude montre que la géométrie de la structure joue un rôle déterminant dans la distribution des contraintes de cisaillement transverses, et que l’effet d’un paramètre d’hétérogénéité tel que ξ est amplifié dans les structures à double courbure, comme les coques sphériques. Ces résultats mettent en évidence l’importance de tenir compte à la fois de la géométrie et des propriétés fonctionnelles du matériau dans l’analyse des contraintes internes.

L’analyse des figures révèle que la contrainte de cisaillement transverse normalisée  _xz atteint des valeurs maximales différentes selon la géométrie considérée et le paramètre ξ, qui représente l’effet d’une hétérogénéité du matériau. Pour la plaque, la contrainte maximale  _xz augmente légèrement avec ξ, passant d’environ 1.02 pour ξ=0 à environ 1.11 pour ξ=0.3. Cette croissance modérée suggère que l’augmentation de ξ réduit la rigidité effective du matériau, nécessitant un effort de cisaillement accru pour équilibrer les déformations induites.

Dans le cas du cylindre, les valeurs maximales sont légèrement plus élevées, allant d’environ 1.06 à 1.14 lorsque ξ croît de 0 à 0.3. Cette hausse plus marquée s’explique par la courbure moyenne du cylindre, qui modifie la répartition des efforts internes et rend la structure plus sensible à l’effet de gradient ou de porosité. Pour la sphère, l’effet combiné de la double courbure et de l’augmentation de ξ est encore plus significatif : la contrainte maximale passe d’environ 1.20 pour ξ=0 à environ 1.29 pour ξ=0.3. La courbure dans deux directions intensifie les concentrations de contraintes de cisaillement, et l’hétérogénéité du matériau accentue encore cette amplification.

Donc, la contrainte maximale de cisaillement transverse  _xz augmente avec le paramètre ξ dans les trois géométries étudiées, avec une intensité croissante de la plaque vers la sphère. Ce comportement met en évidence l’interaction entre la géométrie de la structure et les propriétés variables du matériau, soulignant l’importance d’une modélisation précise pour prédire les réponses mécaniques internes dans des structures complexes.

Questions Fréquemment Posées

Quel est l’effet du potentiel magnétique sur la contrainte normale dans une coque poreuse ?

Les contraintes normales minimales se localisent dans la couche en céramique de la plaque, tandis que les contraintes maximales apparaissent dans la région supérieure de la coque lorsque le potentiel magnétique est positif.

Comment le rapport géométrique influence-t-il la contrainte normale dans les coques ?

À mesure que le rapport R/a décroit, la contrainte maximale en compression devient plus importante, avec une accentuation plus marquée dans le cas des coques sphériques.

Quel est l’impact de la porosité sur la contrainte de cisaillement transverse dans les structures ?

La distribution de la contrainte de cisaillement transverse est quasi parabolique et symétrique pour la plaque, avec une valeur maximale au centre et nulle aux faces libres.