Comment les potentiels électriques influencent-ils les coques FGM en 2023?

L’impact des potentiels électriques sur les coques à double courbure révèle des résultats surprenants : une variation significative des contraintes normales peut transformer notre compréhension des matériaux à gradient fonctionnel. Cette étude offre des perspectives inédites sur le couplage électromagnétique, essentiel pour les applications avancées.

• 1. Effet du potentiel électrique sur la variation de la contrainte  y

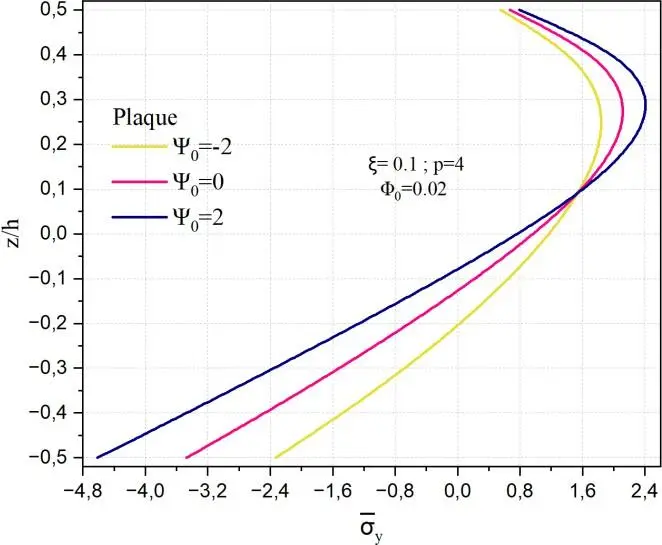
Les Figs.II.10 présentées illustrent la distribution de la contrainte normale moyenne  y à travers

l’épaisseur normalisée z/h de structures en matériau à gradient fonctionnel (FGM) Al/Al₂O₃, soumises à un couplage électromagnétique. Le matériau, composé d’une matrice métallique (Al) enrichie progressivement en alumine (Al₂O₃), présente une variation continue des propriétés mécaniques. Les calculs sont effectués pour un indice de gradient p=4, et des paramètres de couplage magnétique

ξ=0,1,

₀ = 0.02,

en présence d’un potentiel électrique constant et de différentes intensités de

potentiel électrique  ₀ = −2,0,2.

4

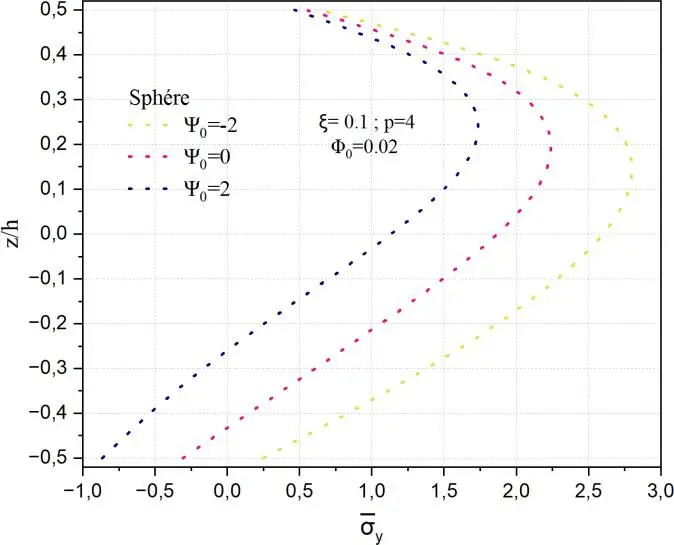
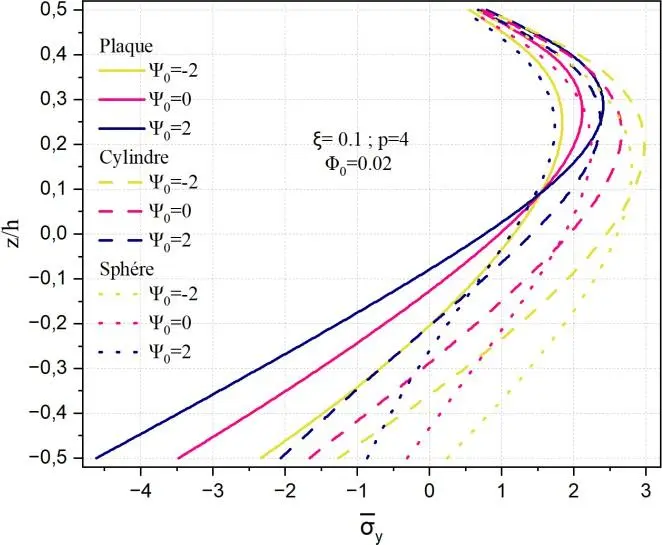
Fig. II.10. Variation de la contrainte normale  y à travers l’épaisseur de la coque en FGM pour

différentes valeurs de potentiel électrique  0 .

Pour la plaque, on note que les contraintes les plus compressives environ −4,8, apparaissent dans la partie inférieure (z/h=−0,5), riche en céramique, tandis que les contraintes en traction atteignent environ 2,4 dans la couche supérieure. Ce déséquilibre marqué entre compression et traction souligne l’influence du champ magnétique appliqué combiné à la variation des propriétés mécaniques. Le champ magnétique négatif intensifie les effets compressifs dans les zones métalliques, plus sensibles à la magnétostriction.

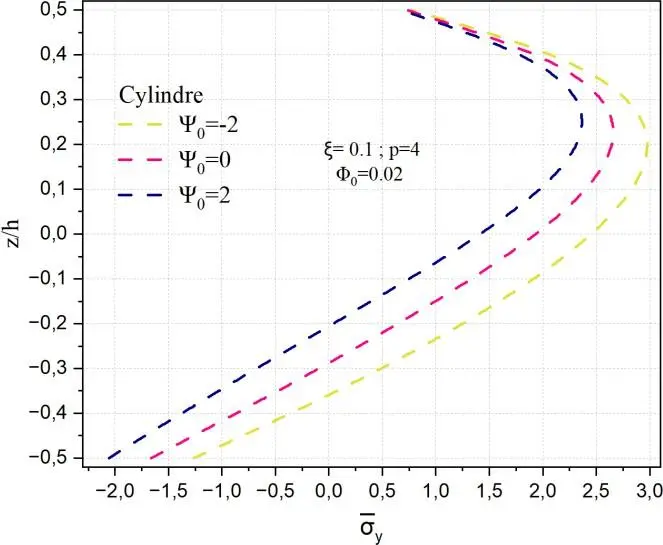
En revanche, dans les structures courbées (cylindriques et sphériques), un comportement inversé est observé : les contraintes maximales en traction sont générées pour un potentiel magnétique positif

 ₀ = 2 . Dans ces cas, la géométrie joue un rôle fondamental. Les contraintes maximales atteignent environ 2,8 pour la coque cylindrique et 2,7 pour la sphérique, tandis que les valeurs en compression restent plus faibles, autour de -2 et -1 respectivement. Cette réponse est attribuable à l’effet de la

courbure, qui modifie la distribution des efforts internes sous l’action du champ magnétique : la

double courbure de la sphère renforce la contrainte de confinement, accentuant la traction au sommet.

Dans toutes les configurations, la distribution de  y est clairement asymétrique, reflet du couplage

multiphysique (électromagnétique et mécanique) dans un matériau FGM. Ces résultats mettent en évidence l’influence conjointe du gradient fonctionnel, du champ magnétique, et surtout de la géométrie de la structure. Ils démontrent que l’ajustement du potentiel magnétique permet de moduler efficacement la répartition des contraintes, offrant ainsi un outil de conception pour le contrôle de la réponse mécanique des structures intelligentes à base de FGM Al/Al₂O₃.

• 1. Effet du potentiel magnétique sur la variation de la contrainte normale  y

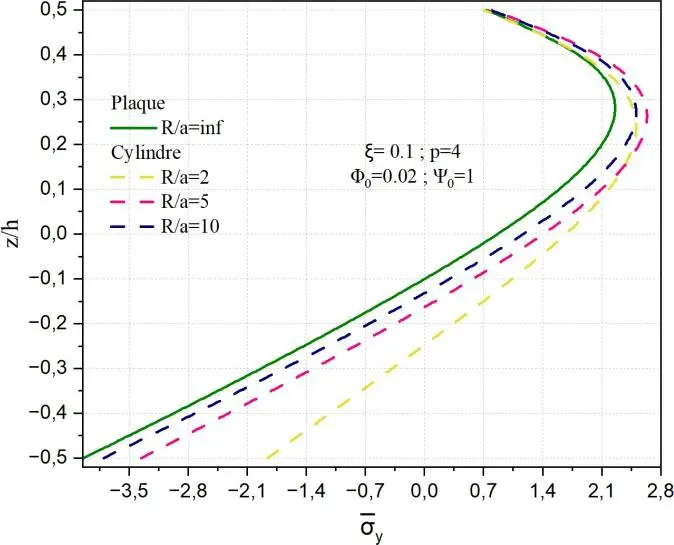
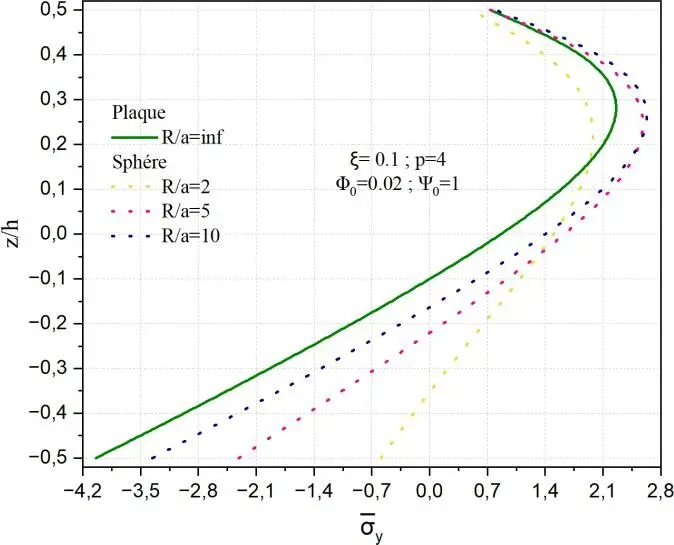
Fig. II.11. Variation de la contrainte normale  y à travers l’épaisseur de la coque en FGM

pour différents rapports géométriques R/a.

La Fig.II.11 montre l’influence du rapport géométrique R/a sur la distribution de la contrainte

normale  y selon l’épaisseur normalisée z/h pour des coques FGM poreuses soumises à un potentiel

électrique constant  ₀ = 1 et un couplage magnétique ₀ = 0.02. La comparaison des résultats entre une plaque (R/a=∞) et des coques sphériques de différents rayons de courbure (rapport R/a=2,5,10), tandis que le graphe de gauche montre le cas équivalent pour des coques cylindriques. On observe

que la courbure a un effet significatif sur l’amplitude et la répartition des contraintes. Au fur et à

mesure que le rapport R/a augmente, la contrainte maximale en compression s’accentue, atteignant environ -4,2 pour la plaque et -0.7 et -2.1 lorsque R/a=2 dans les deux géométries respectivement sphère et cylindre. Cette accentuation est plus marquée dans les coques sphériques que cylindriques pour les grands rapports R/a, ce qui s’explique par une double courbure dans le cas sphérique, induisant un effet de confinement plus important.

À l’opposé, lorsque R/a augmente (vers une plaque), les profils tendent vers celui de la structure plane, avec une augmentation notable de la contrainte maximale dans la couche de céramique. Dans tous les cas, les distributions restent asymétriques à travers l’épaisseur, signe de l’influence conjointe de la porosité, du gradient fonctionnel et de la géométrie.

• 1. Effet de la porosité sur l’évolution de la contrainte transverse  _z

dans les structures

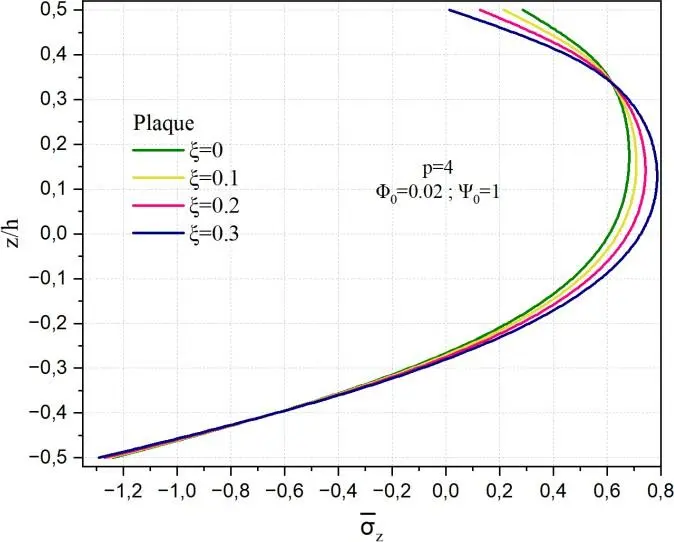
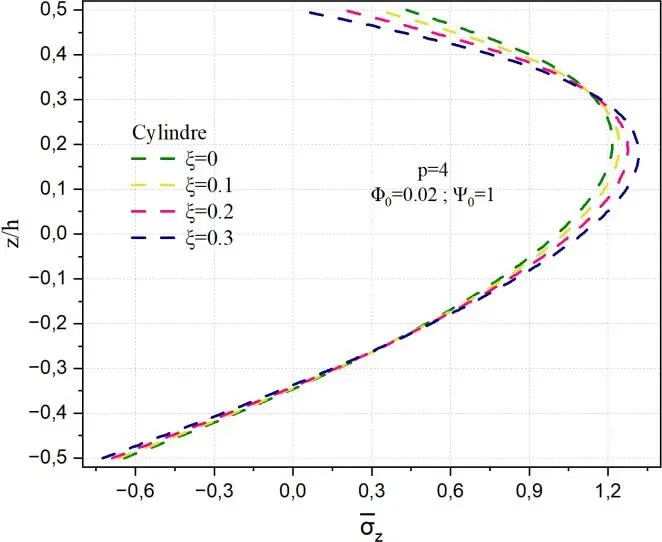
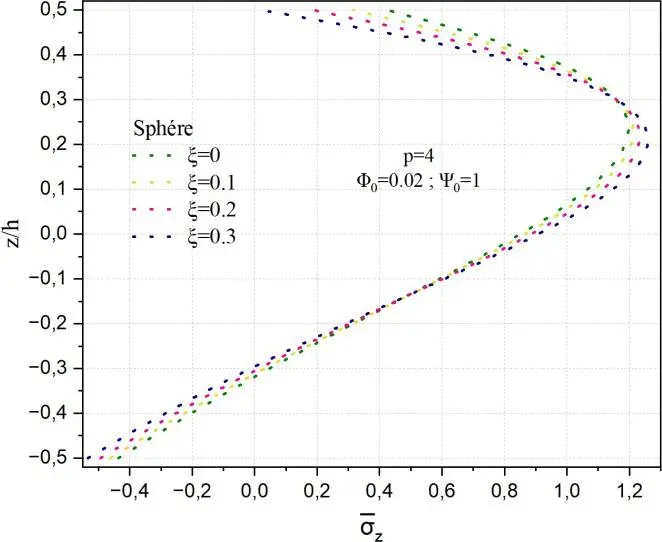
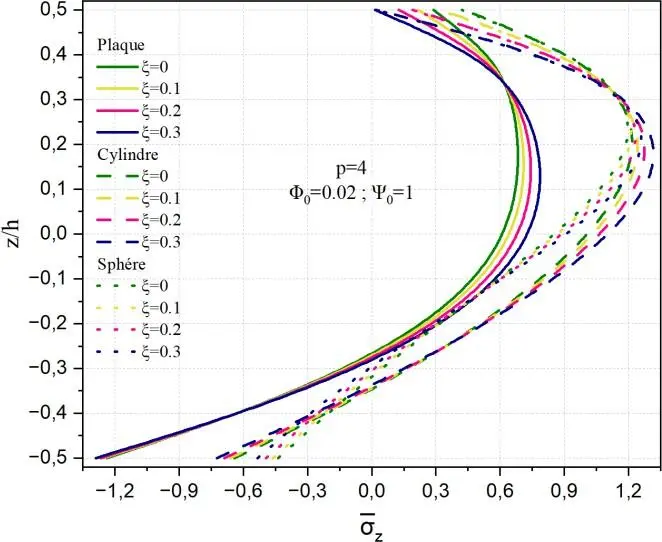
Fig. II.12. Variation de la contrainte normale z à travers l’épaisseur de la coque en FGM pour

différentes valeurs de porosité  .

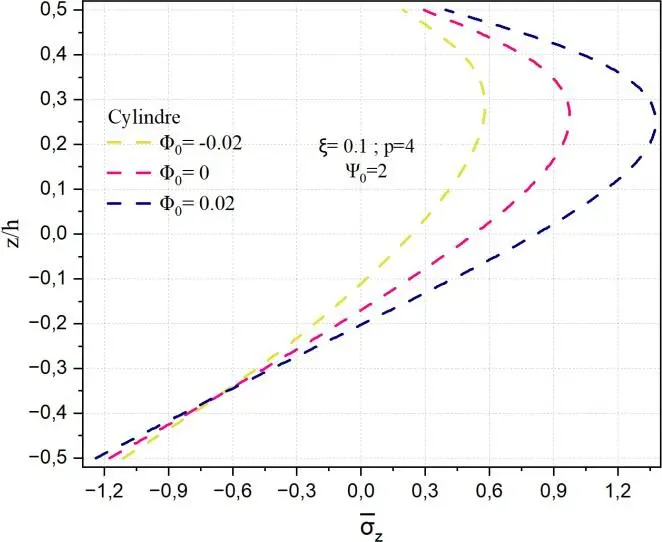
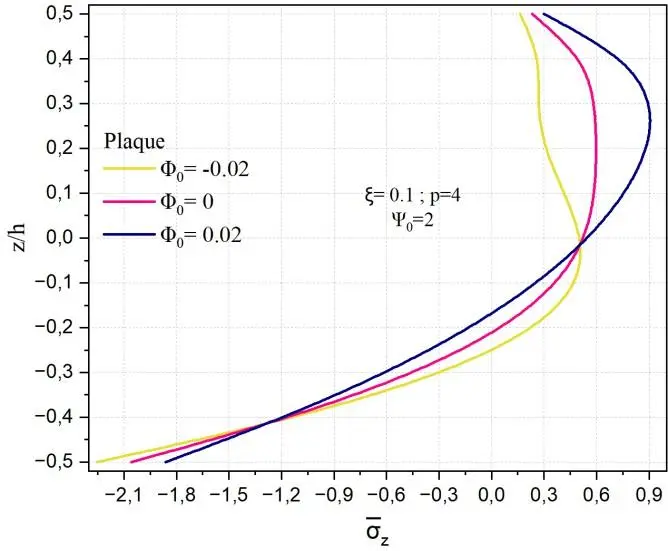
Les Figs. II.12 montrent à travers l’épaisseur respectivement la variation des contraintes normales

transverse  z pour différentes valeurs du facteur de porosité  . Il est à signaler que les allures de

contraintes sont similaires à celles  _x et  _y ainsi elles sont maximales dans la moitié de la partie

supérieure de la coque et minimales au niveau de la surface inférieure de la coque quelle que soit la

porosité. La contrainte normale  z dans la plaque ne dépend pas de  pour deux positions z< -0,2 et

à z≈0,32 alors que, pour les autres structures une position est notée à z≈0,3. La contrainte  z

maximale pour le cylindre et la sphère est de l’ordre de 1.2 à z/h=0.2. La contrainte  z minimale est

de -1.2 à la surface de la céramique. Dans ce cas  _z est plus faible que  _x et  _y .

• 1. Effet du potentiel électrique sur la variation de la contrainte  _z

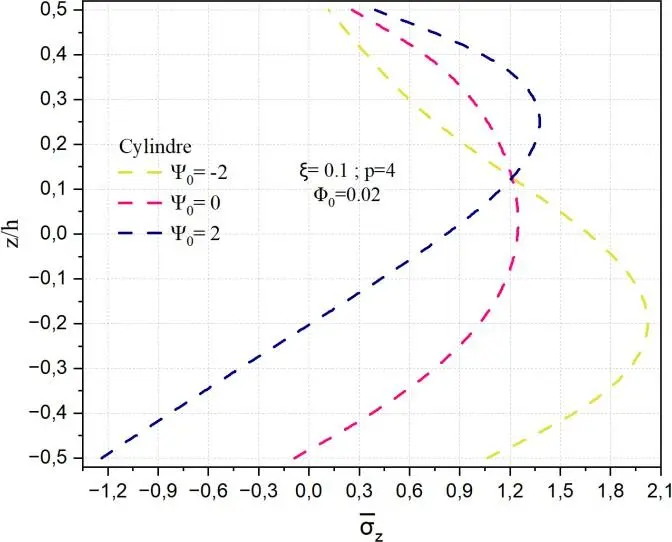
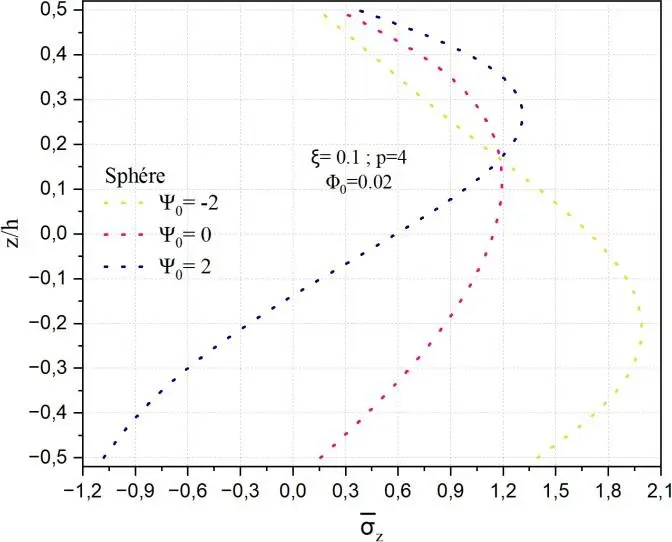
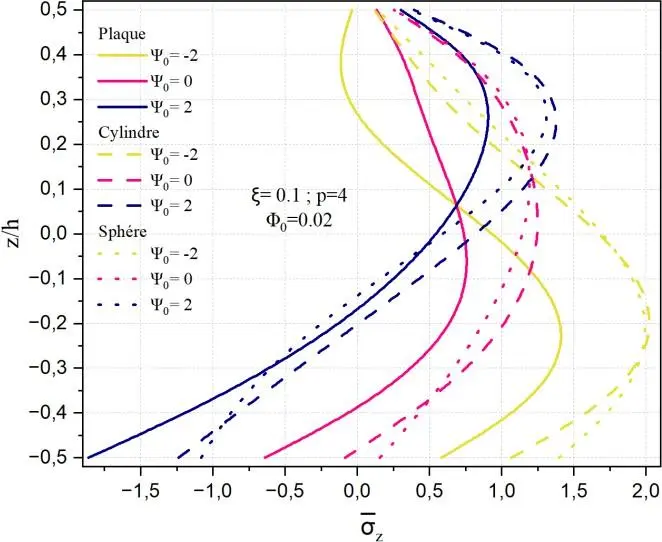
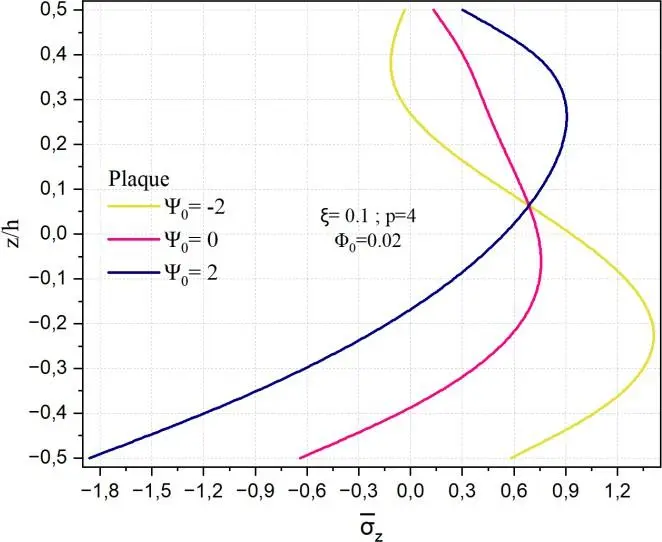
Fig.II.13. Variation de la contrainte normale z à travers l’épaisseur d’une coque en FGM pour

différentes valeurs de potentiel électrique  0 .

La Fig. II.13 met en exergue la distribution de la contrainte normale transverse  _z à travers

l’épaisseur de la structures, plaque, cylindre et sphère, poreuse en matériau à gradient fonctionnel (FGM), pour différentes valeurs du potentiel électrique  ₀ = −2,0,2 avec un indice de puissance p=4,

une porosité 0.1 et un paramètre d’interaction magnétique ₀ = 0.02. Pour la plaque, il apparaît

clairement que le champ électrique a un effet significatif sur le comportement mécanique de la structure en présence du potentiel magnétique constant. Lorsque  ₀ = −2 , la contrainte atteint un minimum d’environ −1.8, indiquant une forte compression dans la partie inférieure de la plaque

(céramique), tandis que pour  ₀ = 2 , la contrainte maximale en traction atteint environ 0.6 au niveau de la surface inférieure (z/h=-0,5). A un potentiel électrique nul  ₀ = 0 la contrainte est de l’ordre de

-0.6. Les contraintes de traction sont faibles au niveau de couche supérieure. A z/h=0.05 la contrainte transverse est indépendante des potentiels électrique et magnétique. Compte tenu des autres structures (cylindrique et sphérique), leur comportement est identique à celui de la plaque, sauf que les valeurs de contrainte sont plus réduites en compression et plus importantes en traction. L’allure de la contrainte normale transverse est asymétrique, visible pour toutes les valeurs du potentiel électrique, résulte de l’interaction entre le champ magnétique, le gradient de composition du matériau et la porosité.

Questions Fréquemment Posées

Comment le potentiel électrique influence-t-il la contrainte normale dans les coques FGM?

Les contraintes les plus compressives apparaissent dans la partie inférieure, riche en céramique, tandis que les contraintes en traction atteignent des valeurs plus élevées dans la couche supérieure, soulignant l’influence du champ magnétique appliqué combiné à la variation des propriétés mécaniques.

Quel est l’effet du rapport géométrique R/a sur la distribution des contraintes dans les coques FGM?

Au fur et à mesure que le rapport R/a augmente, la contrainte maximale en compression s’accentue, atteignant des valeurs différentes selon la géométrie, avec un effet de confinement plus important dans les coques sphériques.

Pourquoi la géométrie des coques affecte-t-elle la réponse mécanique sous un champ magnétique?

La géométrie joue un rôle fondamental car elle modifie la distribution des efforts internes sous l’action du champ magnétique, accentuant la traction au sommet dans les structures courbées.