Les stratégies d’implémentation coques révèlent des résultats surprenants sur la flexion des coques à double courbure, mettant en lumière l’impact crucial de la porosité et des champs électromagnétiques. Ces découvertes transforment notre compréhension des matériaux composites, avec des implications significatives pour l’ingénierie moderne.
Résultats et discussions
Les résultats de la réponse en flexion des coques poreuses, dotée d’une seule couche de PFRC sur la surface supérieure, sont présentés. L’épaisseur de la coque FG est de 1 mm, tandis que celle de la couche PFRC est de 50μm. L’actionneur PFRC est fabriqué à partir de PZT5H et d’époxyde. La charge mécanique considérée dans les calculs est de
q = 100N/m2.
Les propriétés élastiques et piézoélectriques de la couche PFRC, obtenues par Mallik et Ray [97], sont utilisées pour effectuer les calculs numériques.
Qp = 32,6 GPa,
Qp = 4,3 GPa,
Qp = 4,76 GPa,
Qp = 3,85 GPa,
Qp = 7,2 GPa,
Qp = Qp = Qp = 1,29 GPa,
Qp = 1,05 GPa et
e31 = -6,76 C/m2.
Les composantes du matériau FGM sont noté sur la référence [23]. D’après l’analyse micromécanique de Aniket et al.[98], il a été constaté que les valeurs des coefficients piézoélectriques e32, e33, e15 et e24, par rapport au système de coordonnées du matériau, sont beaucoup nettement inférieures, voire négligeable par rapport à e31, et par conséquent ne sont pas prises en compte dans l’évaluation des résultats numériques. Les paramètres adimensionnels qui sont utilisés pour présenter les résultats numériques s’écrivent :
Validation du modèle mathématique
Avant d’étudier la flexion des coques avec un actionneur PFRC, nous vérifions d’abord l’efficacité du modèle en l’absence de cet actionneur, en ne considérant que les coques en aluminium et en céramique. Une valeur des rapports géométriques, tels que longueur/épaisseur (a/h), largeur/longueur (b/a), sont prises en considération avec et sans la couche piézoélectrique.
Les Tableaux II.a et II.b présentent les résultats de la déflexion centrale adimensionnelle des structures, à savoir la plaque, le cylindre et la sphère en métal et en céramique respectivement. Les valeurs de la déflexion de la plaque non poreuse sont comparées à la solution de Benyoucef et al. [93], Thai et Choi [94] et Rachid et al.[23,24]. Les résultats obtenus de la flèche et des contraintes pour la plaque en aluminium et en céramique non poreuse (ξ = 0) sont en parfaite concordance avec ceux fournis par les autres théories quasi-3D de Rachid et al.[23].
L’influence de l’indice de la couche piézoélectrique sur le comportement en flexion des deux plaques (Al, Céramique) a été analysée pour différentes configurations géométriques, plaque, cylindre et sphère. Les résultats montrent une tendance générale à la diminution de la déflexion maximale et des contraintes avec l’activation de la couche piézoélectrique. L’effet du rayon pour les structures cylindre et sphère est mis en évidence pour différents rapports géométriques R/a=2, 3, 5, 10, 20 et 100. La sphère possède le plus faible déplacement transversal.
Tableau II.a. Comparaison des déflexions et les contraintes non dimensionnels d’une plaque carrée en matériau céramique (Al2O3) simplement supportée soumises à une charge sinusoïdale (a=b=10h).
| Tableau II.a | |
|---|---|
| Paramètre/Critère | Description/Valeur |
| Données de comparaison | Résultats de déflexion et contraintes |
| Données complémentaires | |
|---|---|
| Paramètre | Valeur |
| Références | Benyoucef et al. [93], Thai et Choi [94], Rachid et al.[23,24] |
| Configuration géométrique | |
|---|---|
| Paramètre | Valeur |
| a/h | 10 |
| b/a | 1 |
Tableau II.b. Comparaison des déflexions et les contraintes non dimensionnels d’une plaque carrée en matériau métallique (Al) simplement supportée soumises à une charge sinusoïdale (a=b=10h).
| Tableau II.b | |
|---|---|
| Paramètre/Critère | Description/Valeur |
| Données de comparaison | Résultats de déflexion et contraintes |
| Configuration matérielle | |
|---|---|
| Paramètre | Valeur |
| Matériau | Aluminium (Al) |
| Données supplémentaires | |
|---|---|
| Paramètre | Valeur |
| Type de structure | Plaque, cylindre, sphère |
Evolution de la déflexion dans les structures sous l’effet la variation du potentiel électrique ψ0
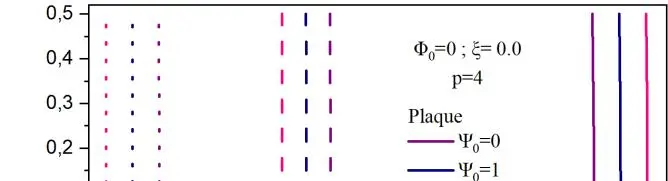
La Fig.II.2 montre l’effet de la variation du potentiel électrique en fonction du déplacement normalisé, pour différentes valeurs du potentielle magnétique. La comparaison est réalisée pour les trois différentes configurations. Il est à remarquer que les plus importants déplacements sont notés sur le couche supérieure de la plaque en FGM, et les plus faibles sont pour la sphère quel que soit le potentiel électrique. Lorsque le potentiel électrique ψ0 = 0 (voir Fig.II.2b) les déplacements sont importants lorsque le potentiel magnétique est nul.
Un comportement inverse se produit pour les structures sphère et cylindre. Le déplacement est minimal lorsque le potentiel magnétique est nul. Sur la Fig.II.2c, on montre la variation du déplacement adimensionnel sur l’épaisseur de la plaque sous différents potentiels électriques et un potentiel magnétique φ0 = 0. Il est à noter que le comportement est totalement inversé par rapport à la Fig.II.2b. En présence de la porosité ξ = 0.1, nous avons tracé sur la Fig.II.3, le déplacement adimensionnel avec les mêmes paramètres de la Fig.II.2.
Il est à constater que les allures sont identiques sauf que la porosité influe sur la dégradation du matériau en causant des valeurs plus importantes des déplacements dû à la déflexion.
Porosité = 0
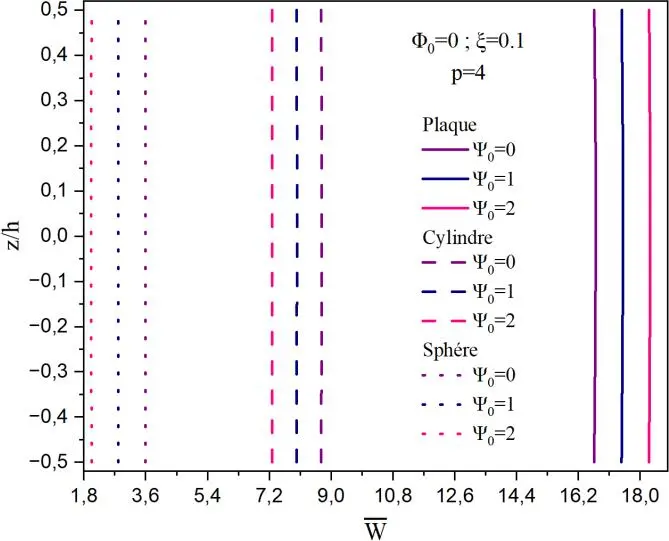
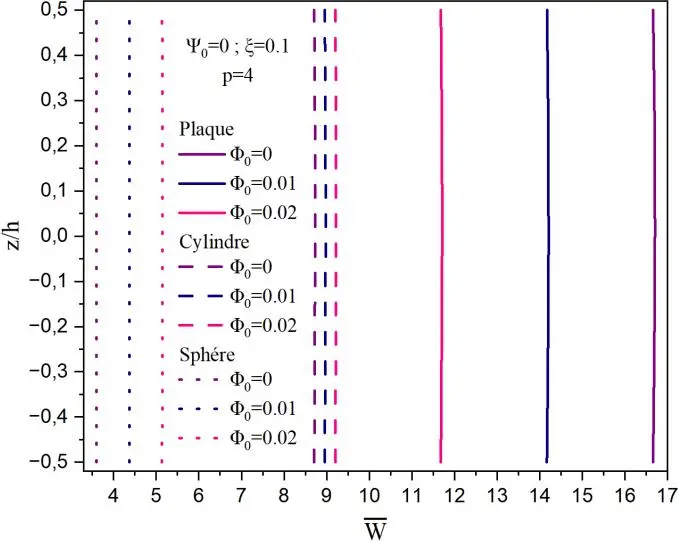
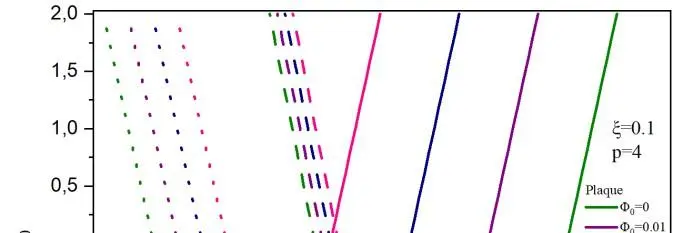
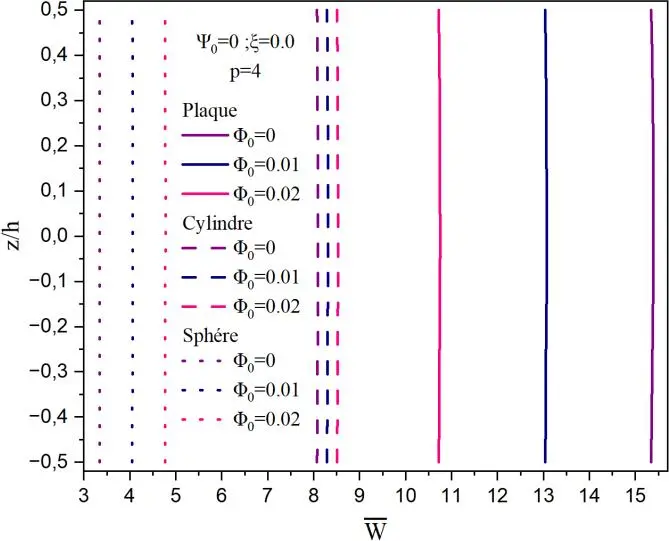
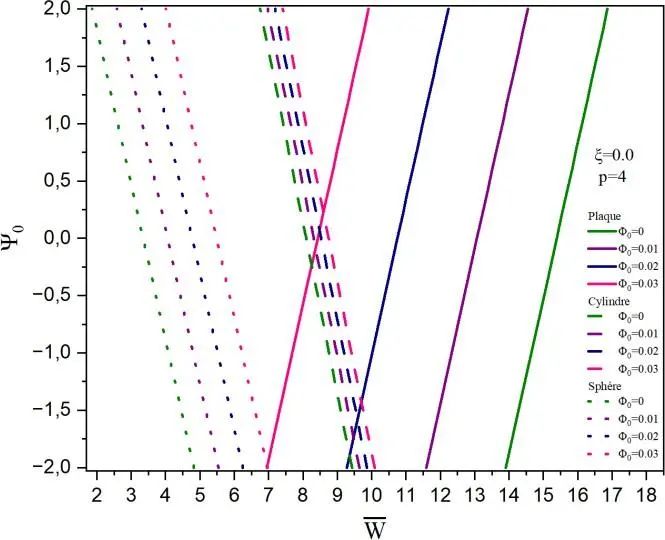
Fig. II.2. Déflexion centrale adimensionnelle de la coque non poreuse en fonction des différents paramètres a) Effet de ψ0 sur la déflexion, b) Effet de φ0 avec ψ0 = 0, c) Effet de ψ0 avec φ0 = 0.
Porosité = 0.1
Fig. II.3. Déflexion centrale adimensionnelle de la coque poreuse en fonction des différents paramètres a) Effet de ψ0 sur la déflexion, b) Effet de φ0 avec ψ0 = 0, c) Effet de ψ0 avec φ0 = 0.
Effet de la porosité sur l’évolution de la contrainte normale σx dans les structures
La Fig. II.4. Exhibe la variation de la contrainte normale σx à travers l’épaisseur de la coque poreuse en FGM pour différentes valeurs de porosité ξ, l’indice de puissance p=4 et un potentiel électrique ψ0 = 1. L’effet de la porosité est mis en évidence.
Il est à remarquer que les contraintes minimales sont dans la couche d’aluminium, elles sont de l’ordre de -4.2 alors que les contraintes maximales de tension 2 sont obtenues dans la partie supérieure à z/h=0.3 pour le cas du potentiel magnétique positif de φ0 = 0.02. La contrainte de compression est de l’ordre de deux fois plus importantes que celle de la traction.
La contrainte maximale pour le cas du cylindre et de la sphère est obtenue z/h=0.25 et 0.2 respectivement. Les plus faibles contraintes sont obtenues pour la sphère et sont nulles sont la surface supérieure. Quelle que soit la forme de la structure l’allure de la contrainte n’est pas symétrique.

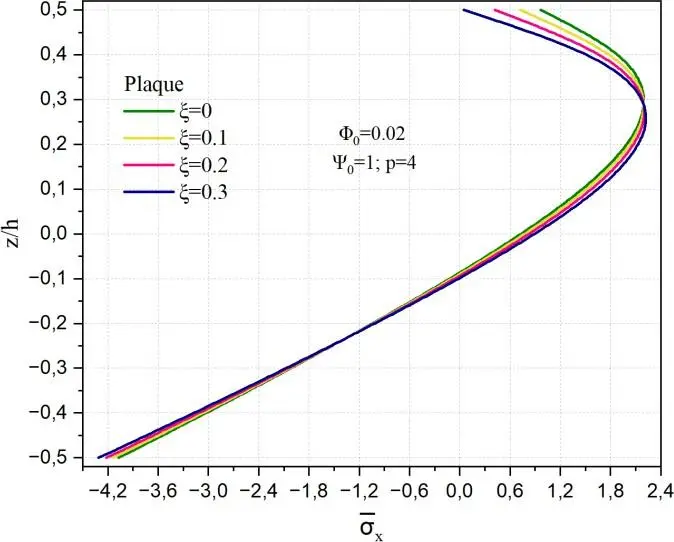
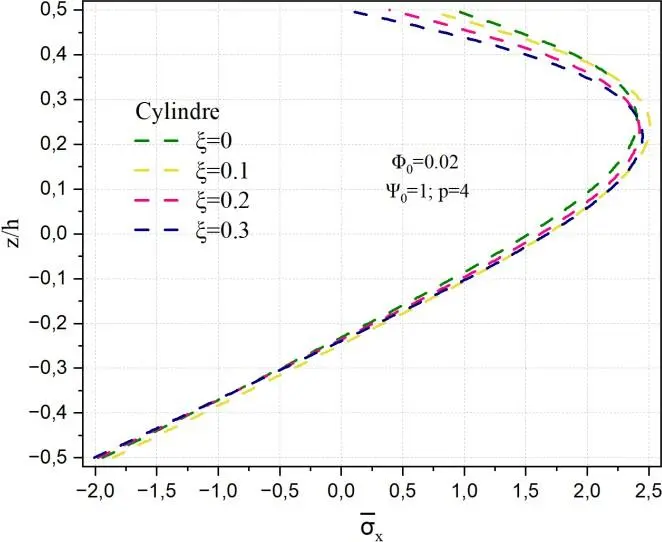
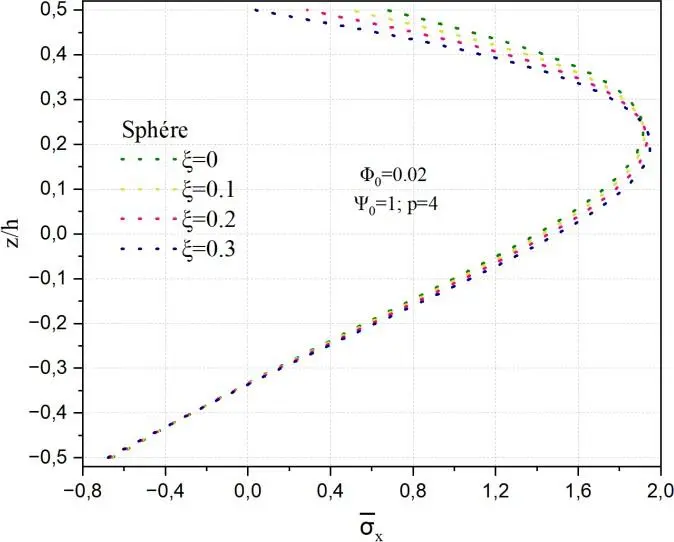
Fig. II.4. Variation de la contrainte normale σx à travers l’épaisseur de la coque poreuse en FGM pour différentes valeurs de la porosité.
Questions Fréquemment Posées
Quelle est l’épaisseur de la coque FG étudiée dans l’analyse?
L’épaisseur de la coque FG est de 1 mm.
Comment l’actionneur PFRC est-il fabriqué?
L’actionneur PFRC est fabriqué à partir de PZT5H et d’époxyde.
Quel est l’effet de la couche piézoélectrique sur la déflexion des coques?
Les résultats montrent une tendance générale à la diminution de la déflexion maximale et des contraintes avec l’activation de la couche piézoélectrique.