L’étude de cas sur les coques FGM révèle que les matériaux composites à double courbure peuvent transformer notre compréhension de la flexion électro-magnéto-élastiques. En explorant l’impact de la porosité et des potentiels électriques, cette recherche offre des solutions innovantes pour des applications d’ingénierie avancées.
Chapitre II
Analyse de la flexion électro-magnéto-élastiques d’une coque à double courbure
- Introduction
Les matériaux composites stratifiés sont les matériaux composites les plus largement utilisés dans les applications d’ingénierie en raison de leurs propriétés attrayantes, telles qu’une masse réduite, une résistance accrue et une flexibilité améliorée. Ils offrent une résistance supérieure à l’usure, à la corrosion, ainsi qu’à d’autres sollicitations mécaniques. Toutefois, leur principal inconvénient réside dans le risque de délamination, dû à la variation abrupte des propriétés aux interfaces des couches.
Cette limitation peut être surmontée par l’utilisation de matériaux à gradient fonctionnel (FGM), dans lesquels les propriétés varient de manière continue selon l’épaisseur de la plaque. Les FGM sont composés généralement de deux matériaux, une céramique et un métal, dont les comportements mécaniques sont distincts et complémentaires, permettant d’obtenir les caractéristiques souhaitées.
Les FGM présentent des propriétés d’ingénierie très diversifiées. Il s’agit de matériaux dont les propriétés — notamment le module de Young, le module de cisaillement, le coefficient de Poisson, la densité et le coefficient de dilatation thermique — varient progressivement dans une ou plusieurs directions. L’amélioration de caractéristiques telles que la conductivité thermique, la résistance à la corrosion, la dureté, la rigidité ou encore la soudabilité est rendue possible grâce à cette variation directionnelle des propriétés. Les gradients de propriétés des FGM sont généralement modélisés à l’aide de lois de distribution telles que la loi en puissance (power law), la loi sigmoïde, la loi exponentielle ou encore la méthode de Mori-Tanaka.
Les FGM trouvent de nombreuses applications dans des secteurs tels que l’énergie nucléaire, les centrales électriques, l’aéronautique, les structures offshores, les coques de fusée, entre autres. De ce fait, leur utilisation dans les travaux de recherche connaît une croissance constante.
Les plaques composites sont analysées à l’aide de différentes théories afin de déterminer leur comportement en flexion sous charges mécaniques et/ou thermiques. Ces théories sont classées en deux catégories : les théories classiques et les théories raffinées. La théorie classique des plaques (CPT), développée par Kirchhoff [64] au XIXe siècle pour l’analyse statique des plaques minces, néglige les effets des contraintes de cisaillement transverse, ce qui conduit à des résultats imprécis pour les plaques composites épaisses où ces effets sont significatifs.
Pour pallier cette lacune, Mindlin [65] a proposé au XXe siècle la théorie de cisaillement de premier ordre (FSDT), qui prend en compte les contraintes de cisaillement transverse pour les plaques minces à modérément épaisses. Toutefois, elle ne satisfait pas les conditions de cisaillement nul sur les surfaces supérieure et inférieure de la plaque, et nécessite un facteur de correction dépendant du problème étudié pour tenir compte de l’énergie de déformation due au cisaillement.

Cela a motivé le développement de théories de cisaillement d’ordre supérieur (HSDT), qui intègrent les effets du cisaillement transverse ainsi que des contraintes normales, tout en respectant les conditions aux limites réalistes en cisaillement sur les surfaces de la plaque. Reddy [66] a ainsi proposé une théorie de cisaillement de troisième ordre satisfaisant les conditions de cisaillement nul.
Ces différentes théories sont largement documentées dans les travaux de Sayyad et Ghugal [67–68]. Swaminathan et Sangeetha [69] ont proposé une analyse critique des diverses méthodes de modélisation et de résolution utilisées dans l’analyse thermique des plaques FGM, tandis que Swaminathan et al. [70] ont passé en revue les méthodes analytiques et numériques appliquées à l’analyse statique, dynamique et au flambement de ces plaques.
Zenkour [71] a établi des relations exactes entre les solutions en flexion de la théorie classique des plaques minces et celles issues de la théorie de déformation par cisaillement sinusoïdale pour les plaques homogènes et FGM. Zhong et Shang [72] ont utilisé la solution de Plevako des équations tridimensionnelles générales pour obtenir des solutions fermées des plaques FGM en 3D.
Zenkour et Alghamdi [73] ont analysé le comportement en flexion de plaques sandwich soumises à des charges thermomécaniques à l’aide de théories d’ordre supérieur. Cinefra et al. [74] ont effectué une analyse thermomécanique de coques FGM simplement appuyées via des théories raffinées pour les coques. Zidi et al. [75] ont étudié la réponse en flexion des plaques FGM reposant sur des fondations élastiques et soumises à des chargements hygro-thermo-mécaniques à l’aide d’une théorie de plaque raffinée à quatre variables.
Sayyad et al. [76] ont appliqué une théorie de cisaillement de plus haut ordre de type exponentiel à l’analyse en flexion de plaques composites laminées à plis croisés soumises à un gradient thermique linéaire. Reddy et Chin [77] ont étudié la réponse thermoélastique dynamique des cylindres et plaques FGM à l’aide d’une formulation par éléments finis.
Garg et al. [78] ont réalisé une analyse de flexion hygro-thermo-mécanique de poutres sandwich FGM symétriques et non symétriques selon les lois de gradation puissance, exponentielle et sigmoïde, en utilisant une théorie en zigzag de plus haut ordre fondée sur la méthode des éléments finis. Ghugal et al. [79] ont appliqué une théorie trigonométrique de déformation par cisaillement et déformation normale pour l’analyse des contraintes thermiques de coques composites stratifiées.
Un modèle d’ordre supérieur a été développé pour l’analyse des vibrations libres des plaques MEE. Xin et Hu [80] ont utilisé une approche semi-analytique basée sur l’espace d’états pour étudier le comportement en vibration libre de poutres MEE multicouches. Bhangale et al. [81] ont adopté une procédure par éléments finis semi-analytique pour examiner les caractéristiques vibratoires des plaques MEE à gradients de propriétés.
Vaezi et al. [82] ont étudié la vibration libre de micropoutres élastiques magnétoélectriques et ont déterminé leur fréquence naturelle et leur charge de flambement. Ren et al. [83] ont utilisé une méthode de lissage nodal basée sur l’interpolation radiale par points pour étudier les réponses statiques des structures MEE dans un champ d’humidité.
Zhou et al. [84] ont appliqué cette même méthode pour considérer l’effet d’un environnement thermique sur les réponses transitoires des structures MEE.
Albarody et al. [85] ont établi un modèle analytique de coques composites thermo-magnéto-électro-élastiques (TMEE) basé sur la théorie de la déformation de cisaillement du premier ordre (FOSD). Mahesh et Harursampath [86] ont étudié le problème de déflexion non linéaire de coques MEE renforcées par des nanotubes de carbone soumises à des charges physiques multiples telles que des charges mécaniques, électriques et magnétiques.
Wu et Tsai [87] ont étudié le comportement statique 3D d’une coque FG-MEE soumise à une charge mécanique, un déplacement électrique et un flux magnétique au moyen d’une méthode asymptotique. Kondaiah et al. [88] ont examiné le comportement de coques cylindriques MEE multi phases soumises à des charges thermiques en utilisant une méthode par éléments finis semi-analytique.
En se basant sur une théorie de déformation de cisaillement d’ordre supérieur, Zhang et Li [89] ont analysé le flambement et la vibration de coques cylindriques circulaires MEE à gradient fonctionnel et soumises à des effets thermo-magnéto-électro-élastiques (FGMETE). En appliquant la théorie de l’élasticité non locale avec gradient de déformation à la théorie classique des coques, Sahmani et al. [90] ont étudié les propriétés de flambement non linéaire dépendantes de la taille et le post-flambement de coques cylindriques composites MEE à l’échelle nanométrique.
Ye et al. [91] ont développé une formulation semi-analytique pour estimer les réponses en flexion magnéto-électro-mécaniques de coques cylindriques composites laminées MEE en utilisant la méthode des éléments finis à frontière réduite (SBFEM). Akbarzadeh et al. [92] ont obtenu des solutions en forme fermée pour les réponses multiphysiques d’un cylindre creux MEE en rotation.
Dans ce chapitre, nous avons développé un modèle mathématique HSDT couplé avec le champ magnéto-électro-élastique pour l’analyse statique des coques à double courbure en FGM. Le modèle multiphysique couplé est établi sur la base de la théorie de la déformation de cisaillement d’ordre élevé. Le modèle est d’abord validé à l’aide d’exemples issus de la littérature. Par la suite, des études paramétriques sont menées afin d’illustrer l’influence, de la courbure des coques, le déplacement transversal centré, la variation des contraintes normales et transversales et l’indice de puissance.
- Description des coques à double courbure poreuses FG
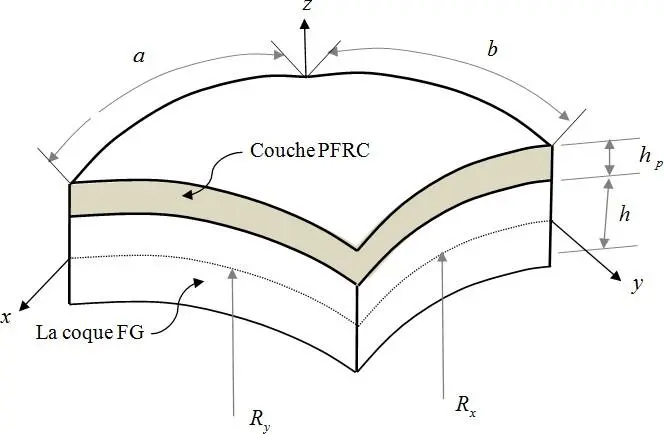
Une coque FG en céramique et en métal est considérée dans ce chapitre. La Fig. II. 1 présente les dimensions de la coque, longueur a, largeur b et épaisseur h avec le système de coordonnées adopté (x, y, z). La surface de référence est la surface médiane de la coque définie par z =0 sur l’axe z au plan (xy). La coque FG est reliée à la surface supérieure par un actionneur PFRC d’épaisseur hp. Cette coque est soumise à une charge électrique 0 (x, y), une charge magnétique 0 (x, y) mécanique q(x, y).
Source: URL
Fig. II. 1. Schéma de la coque poreuse FG avec une seule couche PFRC.
Dans la coque à double courbure en FGM on suppose la présence des porosités réparties sur tout le volume en raison de défauts de production. La distribution de la porosité est modélisée à l’aide de deux fonctions différentes caractérisant les propriétés mécaniques qui s’écrivent par Zenkour [73] :
z 1 2
p
E(z) Em
e h 2 1 ,
z 1 2
II.1
p
(z) h 2 1 ,
e
m
E(z)
E E z
c m h
1 p
2
p
Em
E E
c m 2
II.2
(z) z 1
2
Questions Fréquemment Posées
Qu’est-ce qu’une coque à double courbure en matériaux FGM?
Les coques à double courbure en matériaux FGM sont des structures composites stratifiées dont les propriétés varient de manière continue selon l’épaisseur, généralement composées d’une céramique et d’un métal.
Pourquoi utiliser la théorie raffinée de déformation par cisaillement (HSDT) pour l’analyse des coques FGM?
La théorie raffinée de déformation par cisaillement (HSDT) intègre les effets du cisaillement transverse et respecte les conditions aux limites réalistes, ce qui est essentiel pour des plaques composites épaisses.
Comment la porosité influence-t-elle la flexion des coques FGM?
Une analyse paramétrique explore l’influence du paramètre de porosité sur la réponse des coques, indiquant que la variation de porosité peut affecter le comportement électro-magnéto-élastique en flexion.