Les applications pratiques des onduleurs révèlent des avancées surprenantes dans la conduite de machines asynchrones. Cette étude innovante explore des stratégies de commande qui transforment la performance des systèmes électriques, offrant des solutions critiques pour l’industrie moderne.
Simulation et interprétation
La simulation numérique permet de modéliser, d’analyser et de simuler les systèmes dans le domaine de la machine électrique avec beaucoup de précision. De nos jours, il existe toute une panoplie de logiciels pour simuler. Nous avons opté pour le logiciel
« MATLAB/SIMULINK ».
Résultats de simulation
350 0.4
Source: URL
Source: URL

Source: URL
Source: URL
Source: URL
Source: URL
300
0.2
0
250
-0.2
200
wr [rad/s]
Phrd [Wb]
-0.4
150
-0.6
100
-0.8
50 -1
0
0 0.5 1 1.5 2 2.5 3
t [s]
-1.2
0 0.5 1 1.5 2 2.5 3
t [s]
70 1.2
60 1
50 0.8
40 0.6
30 0.4
Cem [N.m]
Phrq [Wb]
20 0.2
10 0
0 -0.2
-10
0 0.5 1 1.5 2 2.5 3
t [s]
-0.4
0 0.5 1 1.5 2 2.5 3
t [s]
6
ia1 ia2
4
2
ia1 & ia2 [A]
0
-2
1.4
-4
-6
2 2.005 2.01 2.015 2.02 2.025 2.03 2.035 2.04
t [s]
25
20
15
10
5
ia1 & ia2 [A]
0
ia1 ia2
1.2
1
0.8
Phr [Wb]
0.6
0.4
-5 0.2
-10
-15
-20
0
0 0.5 1 1.5 2 2.5 3
t [s]
-25
0 0.5 1 1.5 2 2.5 3
t [s]
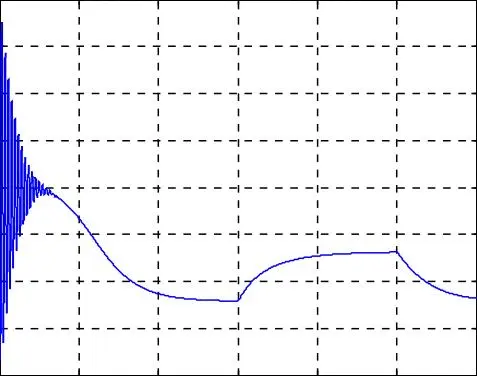
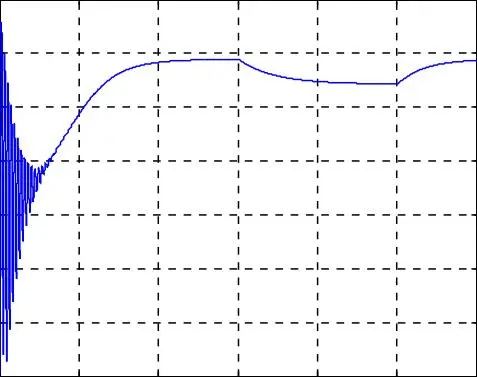
Fig. I.7. Résultats de simulation du modèle de la machine asynchrone double étoile avec un démarrage à vide puis application d’une charge (Cr =14 Nm) entre 1.5 et 2.5 s.
20 1.6
Source: URL
Source: URL
Source: URL
Source: URL
Source: URL
Source: URL
15 1.4
Phrd réf Phrd
10 1.2
5 1
Cem réf [N.m]
Phrd réf & Phrd [Wb]
0 0.8
-5 0.6
-10 0.4
-15 0.2
-20
0 0.5 1 1.5 2 2.5 3
t [s]
0
0 0.5 1 1.5 2 2.5 3
t [s]
25
Cem réf
20 Cem
15
10
Cem réf & Cem [N.m]
5
0.8
0.6
0.4
Phrq réf & Phrq [Wb]
0.2
Phrq réf
Phrq
0 0
-5
-10
-15
-0.2
-0.4
-20
0 0.5 1 1.5 2 2.5 3
t [s]
-0.6
0 0.5 1 1.5 2 2.5 3
t [s]
10
ia1
8 a2
6
4
2
ia1 & ia2 [A]
1.6
1.4
1.2
1
Phr réf & Phr [Wb]
Phr réf
Phr
0 0.8
-2 0.6
-4
0.4
-6
-8 0.2
-10
1.45 1.46 1.47 1.48 1.49 1.5 1.51 1.52 1.53 1.54 1.55
t [s]
0
0 0.5 1 1.5 2 2.5 3
t [s]
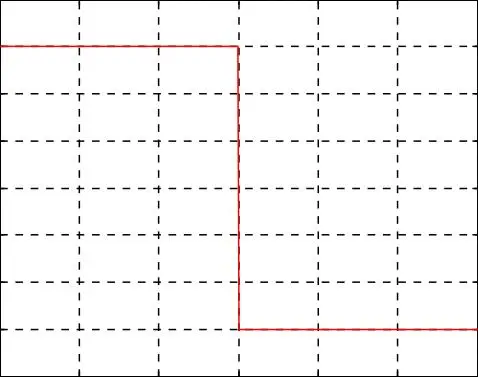
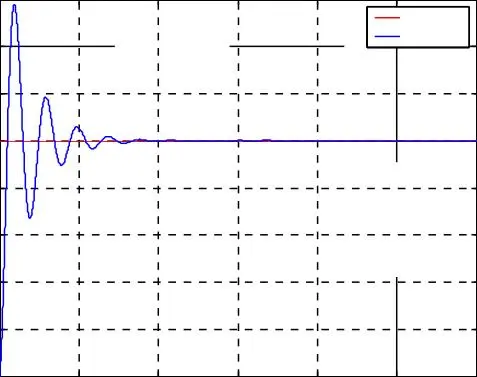
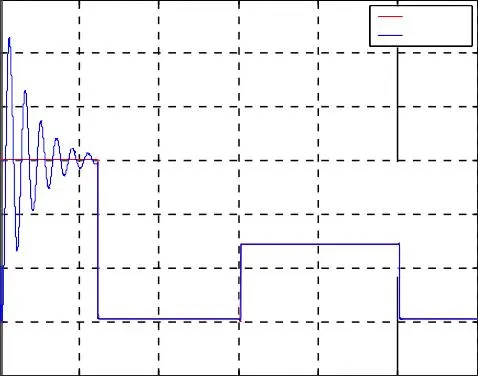
Fig. I.8. Résultats de simulation de la commande vectorielle indirecte sans réglage de vitesse de la MASDE
300
Source: URL
Source: URL
Source: URL
Source: URL
Source: URL
250
Wr réf
Wr
wr réf wr
1.8
1.6
1.4
Phrd réf
Phrd
200 1.2
wr réf & wr [rad/s]
Phrd réf & Phrd [Wb]
1
150
0.8
100 0.6
0.4
50
0.2
0
0 0.5 1 1.5 2 2.5 3
t [s]
0
0 0.5 1 1.5 2 2.5 3
t [s]
60
Cem réf Cem
50
40
Cem réf & Cem [N.m]
30
1
0.8
0.6
0.4
Phrq réf & Phrq [Wb]
0.2
Phrq réf
Phrq
20 0
-0.2
10
-0.4
0
-0.6
-10
0 0.5 1 1.5 2 2.5 3
t [s]
-0.8
0 0.5 1 1.5 2 2.5 3
t [s]
6
ia1 ia2
4
2
0
-2
-4
-6
2.005 2.01 2.015 2.02 2.025 2.03 2.035 2.04
15
10
ia1 ia2
1.8
1.6
1.4
1.2
Phr réf & Phr [Wb]
1
Phr réf Phr
0.8
5
0.6
ia1 & ia2 [A]
0 0.4
-5
-10
0.2
0
0 0.5 1 1.5 2 2.5 3
t [s]
-15
0 0.5 1 1.5 2 2.5 3
t [s]
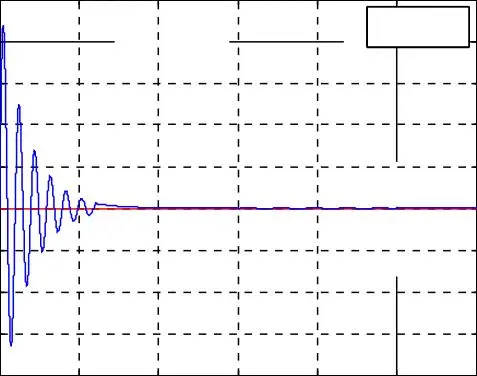
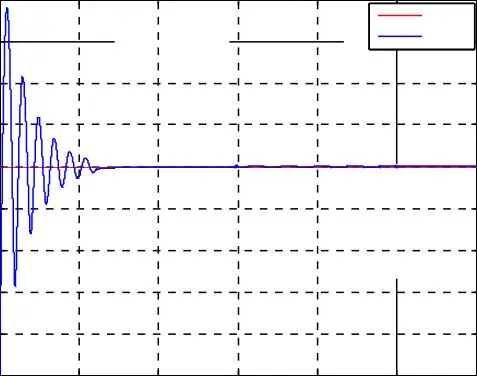
Fig. I.9. Résultats de simulation de la commande vectorielle indirecte avec réglage de vitesse de la MASDE pour une vitesse de référence égale à la vitesse nominale 288 rad/s, avec une réponse
à une perturbation du couple résistant entre 1.5 et 2.5 s.
150
Source: URL
Source: URL

Source: URL
Source: URL
Source: URL
100
wr
wr réf
1.8
1.6
1.4
Phrd réf
Phrd
50 1.2
wr réf & wr [rad/s]
Phrd réf & Phrd [Wb]
1
0
0.8
-50 0.6
-100
0.4
0.2
-150
0 0.5 1 1.5 2 2.5 3
t [s]
0
0 0.5 1 1.5 2 2.5 3
t |s]
60
50
40
30
Cem réf & Cem [N.m]
20
10
0
-10
-20
-30
Cem réf Cem
1
0.8
0.6
0.4
Phrq réf & Phrq [Wb]
0.2
0
-0.2
-0.4
-0.6
Phrq réf
Phrq
-40
0 0.5 1 1.5 2 2.5 3
t [s]
-0.8
0 0.5 1 1.5 2 2.5 3
t [s]
6
ia1 ia2
4
2
ia1 & ia2 [A]
0
-2 1.8
-4
1.6
Phr réf Phr
-6
2 2.05 2.1 2.15 2.2
t [s]
15
10
ia1 ia2
1.4
1.2
Phr réf & Phr [Wb]
1
0.8
5
0.6
ia1 & ia2 [A]
0 0.4
-5
-10
0.2
0
0 0.5 1 1.5 2 2.5 3
t [s]
-15
0 0.5 1 1.5 2 2.5 3
t [s]
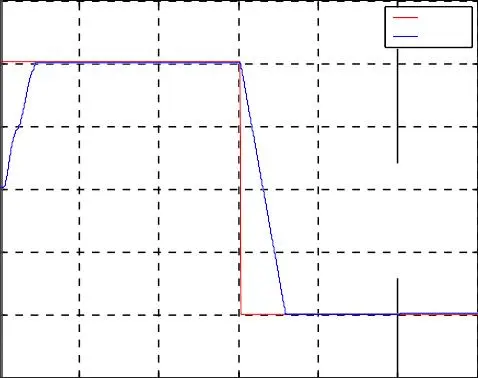
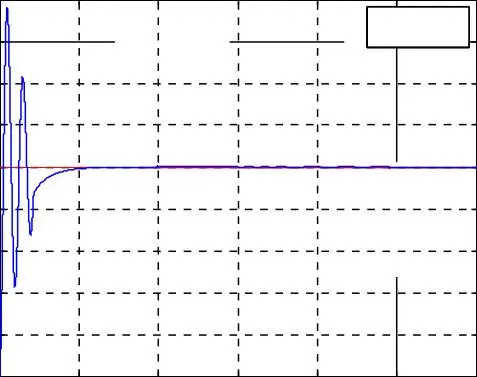
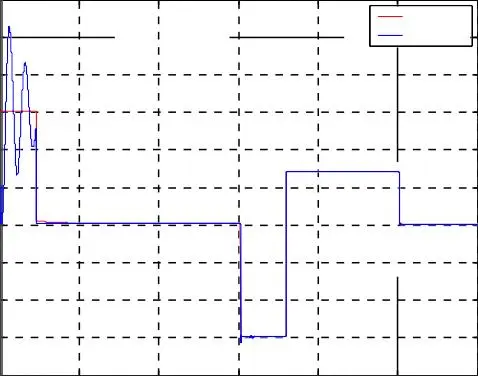
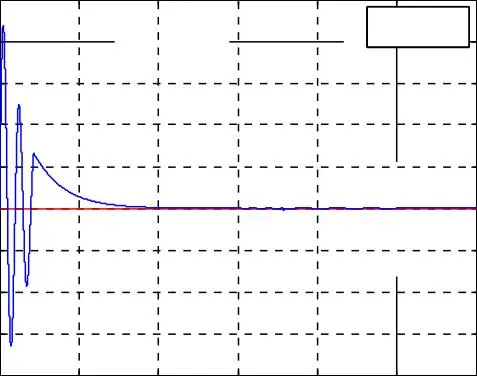
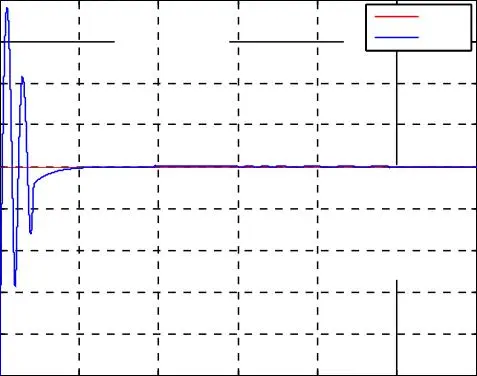
Fig. I.10. Résultats de simulation de la commande vectorielle indirecte avec réglage de vitesse de la MASDE pour une inversion de la vitesse de référence égale de 100 rad/s, avec une réponse à une perturbation du couple résistant entre 1.5 et 2.5 s.
Interprétation des résultats
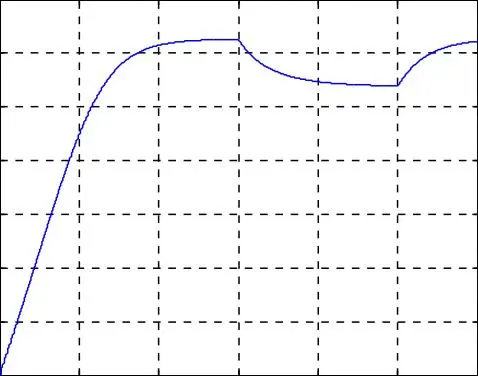
Les résultats obtenus par simulation du modèle de la MASDE lors de l’application d’un couple nominal Cr=14 N.m dans l’intervalle du temps [1.5-2.5] s, sont représentés par la figure I.7 :
A vide
Après un temps de réponse de s où les différentes grandeurs (couple, flux et courant) se stabilisent définitivement, la vitesse de rotation r atteint une valeur proche de la vitesse de synchronisme (314 rad/s).
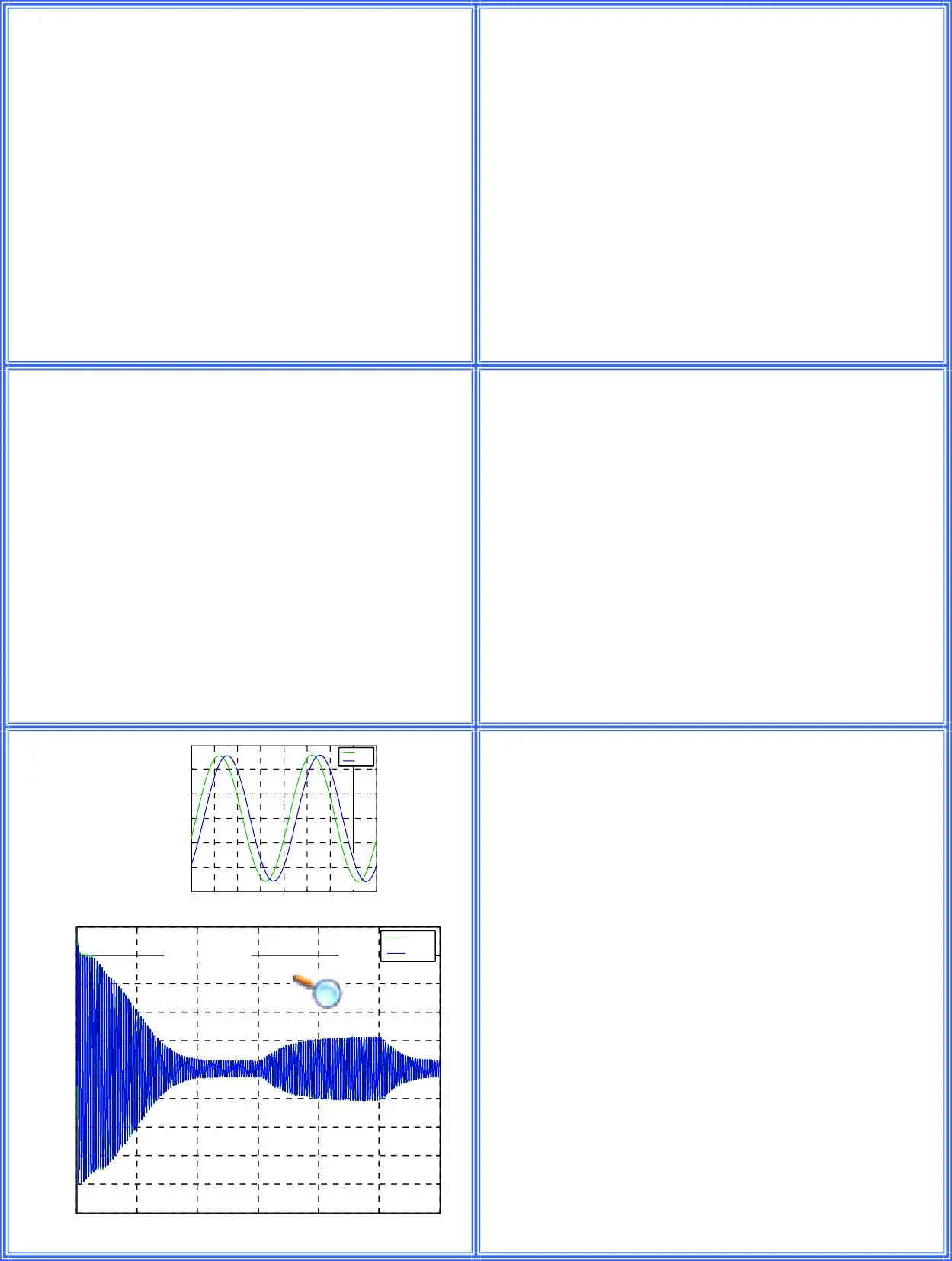
Le courant de phase ia1 varie au démarrage en augmentant jusqu’à 20 A.
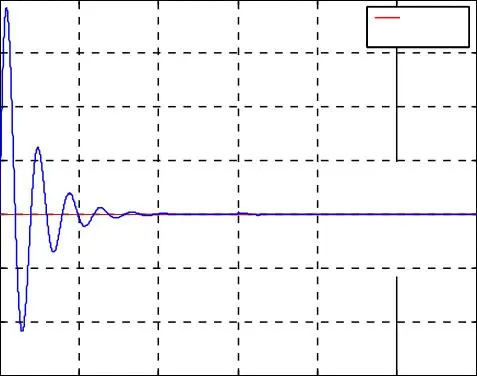
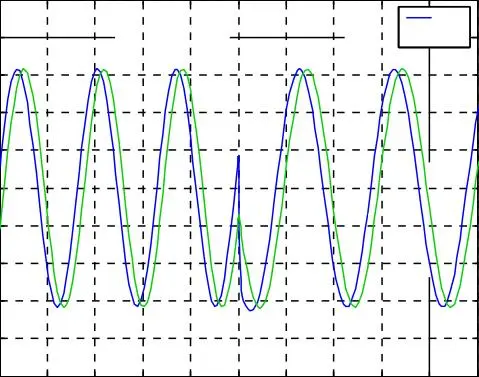
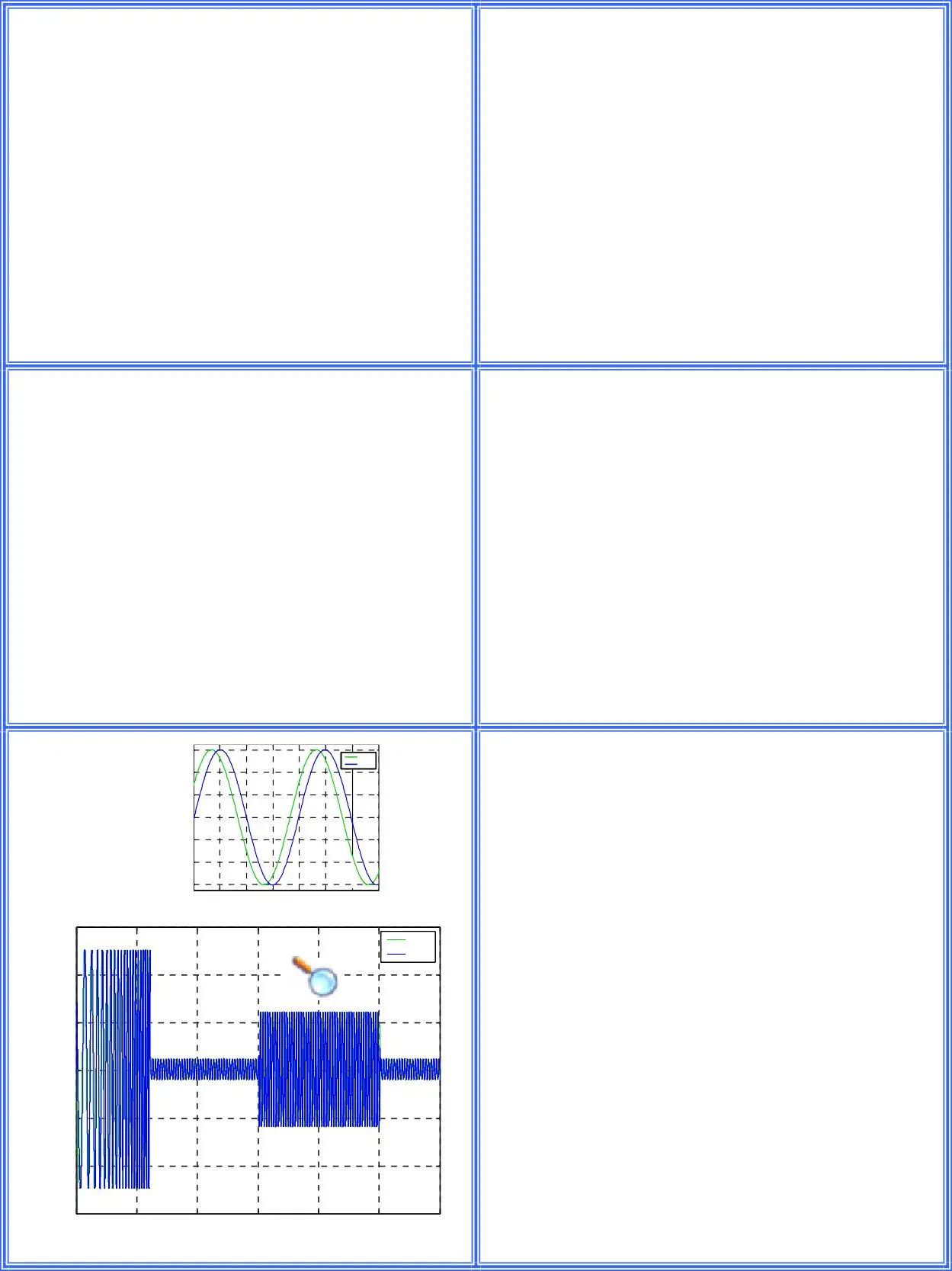
Les courants des deux phases ia1 & ia2 sont sinusoïdaux et parfaitement en quadrature.
Le couple électromagnétique présente des oscillations au démarrage à vide atteignant une valeur maximale de 63 N.m. Cela est nécessaire pour vaincre l’inertie du moteur, puis il revient à une valeur presque nulle à cause de la présence des couples résistants internes (couple de frottement sec et couple de ventilation) en régime permanent.
En charge
L’application de la charge provoque une diminution de vitesse traduite par un glissement. Diminution du flux rotorique résultant (f r ), accroissement de ses composantes ;
en quadrature f rq et directe f rd .
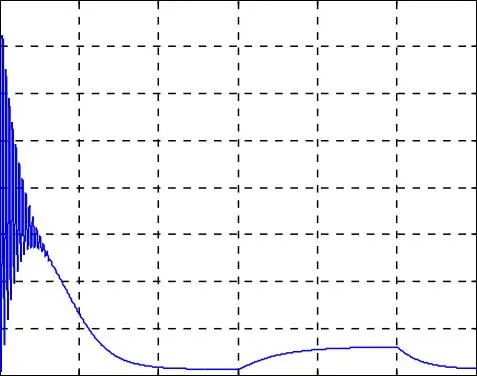
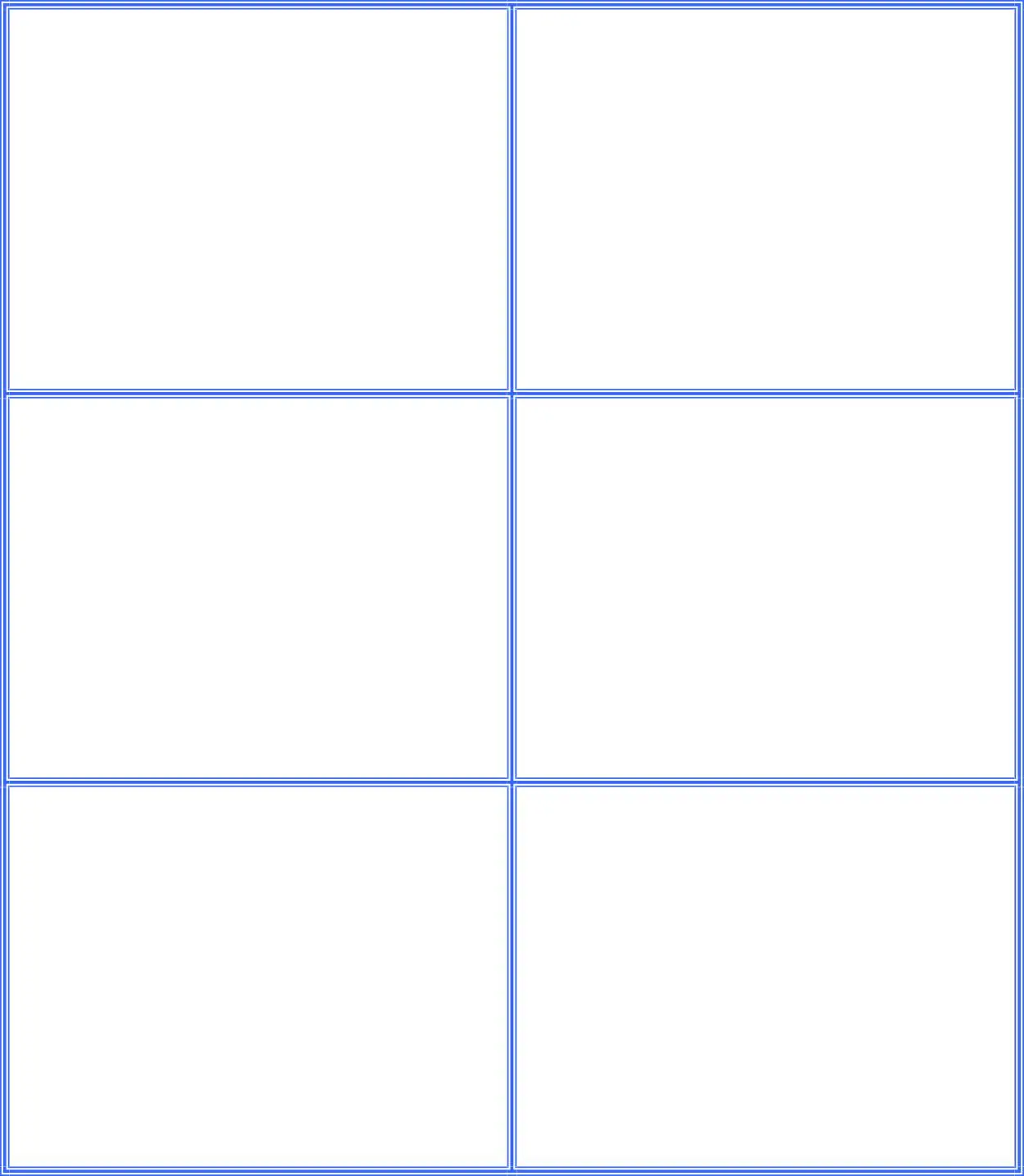
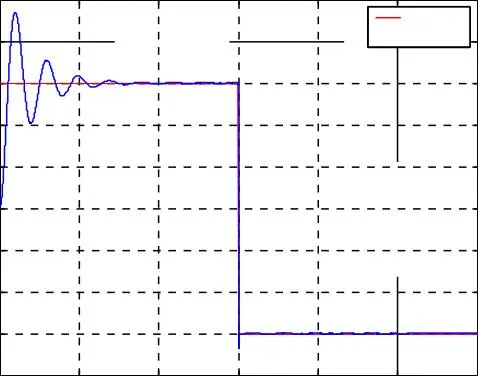
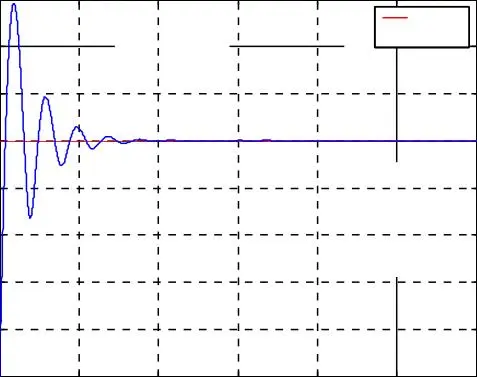
Les résultats de simulation du découplage entre le couple et le flux représentés par la figure I.8, montrent que le couple électromagnétique suit le couple de consigne imposé dans le régime permanant, et le flux rotorique direct se stabilise à la valeur de référence. Nous notons aussi que, malgré la variation brusque du couple électromagnétique, le flux rotorique représenté par les composantes reste constant ce qui montre que le découplage entre le flux et le couple est assuré.
Les figures I.9, I.10 et I.11 représentent les résultats de simulation de la commande vectorielle de la MASDE en imposant un flux de référence égal (1Wb) qui correspond au flux nominal de la machine, pour les trois consignes de vitesse :
La consigne de vitesse est égale à la vitesse nominale, avec une perturbation de charge, correspondante au couple nominale appliquée entre (1.5 et 2 s) figure I.9.
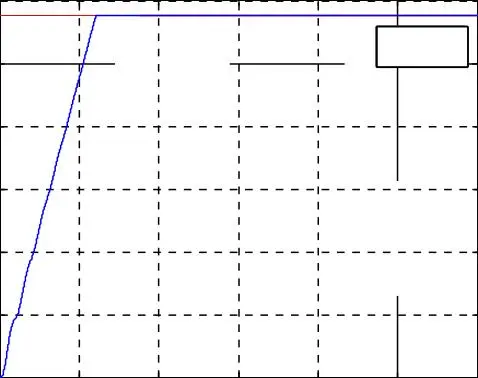
La vitesse suit bien sa consigne, sans la dépasser au bout de 0.61s.
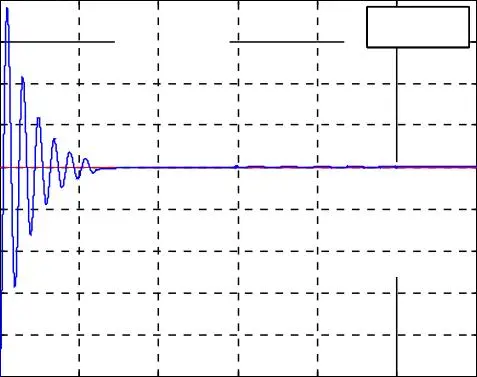
Le couple électromagnétique présente un démarrage oscillatoire atteignant une valeur maximum de 51 Nm.
La composante en quadrature f rq du flux rotorique est nulle, et la composante directe f rd
du flux rotorique est égale au flux rotorique qui suit bien sa valeur de référence à 1 Wb.
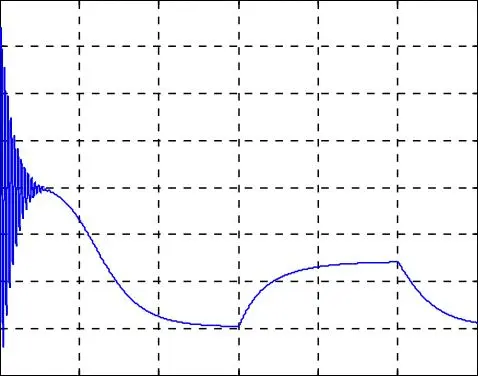
La consigne de vitesse est égale à 100 rad/s avec inversion de sens de rotation à t = 1.5 s avec une perturbation de charge, correspondante au couple nominale appliquée entre (1.5 et 2 s) figure I.10.
La vitesse de rotation suit parfaitement la vitesse de référence imposée.
Présence des perturbations aux niveaux du couple et du courant à l’instant d’inversion de la vitesse.
La composante en quadrature f rq du flux rotorique est nulle, et la composante directe f rd du flux rotorique est égale au flux rotorique qui suit bien sa valeur de référence à 1 Wb donc le défluxage est assuré.
La consigne de vitesse variable de la vitesse nominale de 288 rad/s à 400 rad/s avec une perturbation de charge, correspondante au couple nominale appliquée entre (1.5 et 2 s) figure I.11.
Le découplage entre le couple et le flux est maintenu.
La vitesse de rotation atteint 400 rad/s après 0.47s, pendant ce temps on a une augmentation de courant absorbé et un affaiblissement du flux rotorique direct donc du flux rotorique résultant.
L’application d’une charge ne perturbe ni la vitesse de rotation ni le flux.
Le régulateur PI donne des résultats satisfaisants par rapport à la grandeur de perturbation.
Conclusion
Cette première partie de ce chapitre a été consacrée à la modélisation de la MASDE, avec certaines hypothèses simplificatrices.
A l’aide de la transformation de PARK, nous avons obtenu un modèle dans un repère biphasé lié au champ tournant.
A partir de ce modèle, nous avons effectué une représentation sous forme de variables d’état qui nous a permis d’avoir une description de la dynamique de la MASDE.
Les résultats obtenus par simulation ont permis de mettre en évidence le fort couplage entre les variables internes de la machine (flux, couple).
La seconde partie est consacrée à la présentation de la commande indirecte par flux orienté d’une MASDE. Grâce à une configuration particulière du vecteur flux rotorique, le contrôle vectoriel permet d’assurer un découplage entre les deux variables principales de la machine : le flux et le couple électromagnétique. Ceci permet de réaliser un réglage séparé du flux rotorique et du couple comme cela existe dans la machine à courant continu à excitation séparée.
Le rôle d’un régulateur est de maintenir une grandeur de sortie égale à sa grandeur de référence imposée malgré la présence des perturbations internes ou externes.
Voyant maintenant les performances de la MASDE lorsque l’alimentation est assurée par deux onduleurs de tension à cinq niveaux à cellules imbriquées, où nous définissons d’abord le modèle de connaissance afin de concevoir les stratégies de commande.
Questions Fréquemment Posées
Comment fonctionne un onduleur à cinq niveaux dans les applications pratiques des machines asynchrones?
L’étude présente l’analyse d’un onduleur triphasé multiniveau à 5 niveaux à cellules imbriquées pour l’entraînement de machines électriques de forte puissance.
Quelles sont les stratégies de commande du convertisseur étudiées dans l’article?
La recherche explore deux stratégies de commande du convertisseur : triangulo-sinusoidale et modulation vectorielle avec quatre porteuses bipolaires.
Quel logiciel est utilisé pour la simulation de la machine asynchrone dans l’étude?
Nous avons opté pour le logiciel « MATLAB/SIMULINK » pour modéliser, analyser et simuler les systèmes dans le domaine de la machine électrique.