Le système hybride de production électrique pourrait révolutionner l’approvisionnement énergétique au Cameroun. En combinant l’énergie solaire et hydraulique, cette étude révèle des capacités de production impressionnantes, tout en réduisant les émissions de CO2, avec des implications cruciales pour le développement durable dans les zones rurales.
CHAPITRE III : MODELISATION ET SIMULATION DU MICRO-
SYSTEME HYBRIDE DE PRODUCTION D’ENERGIE ELECTRIQUE (MSHPEE) SOUS L’ENVIRONNEMENT MATLAB/SIMULINK ELECTRIQUE (SHPEE)
INTRODCUTION
L’étude et le dimensionnement du MSHPEE ont permis de choisir les principaux éléments (équipements) nécessaires pour la mise en œuvre de la micro-centrale hybride (MCH) proposé pour le CETIC de Ngang. Etant donné que nous avons un principal système de production qu’est le solaire et un système de secours qu’est l’hydraulique, et un système de stockage d’énergie électrique, comment les combiner pour assurer un approvisionnement ininterrompu en électricité ?
Est-il est possible de les combiner ? Quels sont les outils numériques (logiciels) disponibles pour effectuer des modélisations et simulations numérques? Voilà, les principales préoccupations autour desquelles, ce présent chapitre est introduit dans ce travail, et pour y apporter les éléments de réponses à celles-ci, nous nous focaliserons inéluctablement à la modélisation et à la simulation du MSHPEE proposé sous l’énvironnement MATLAB/SIMULINK qu’est l’outil virtuel de l’ingénierie.
PRESENTION DU MSHPEE
La figure III.1 ci-dessous illustre la configuration du MSHPEE proposé. Il est constitué d’un système solaire, d’un système de turbinage, d’un système de pompage, d’un système de stockage, d’un convertisseur universel et d’une charge.
CA CC

PV
HYDRO
MOTO-POMPE
CONVERTISSEUR UNIVERSEL
CHARGE BATTERIE
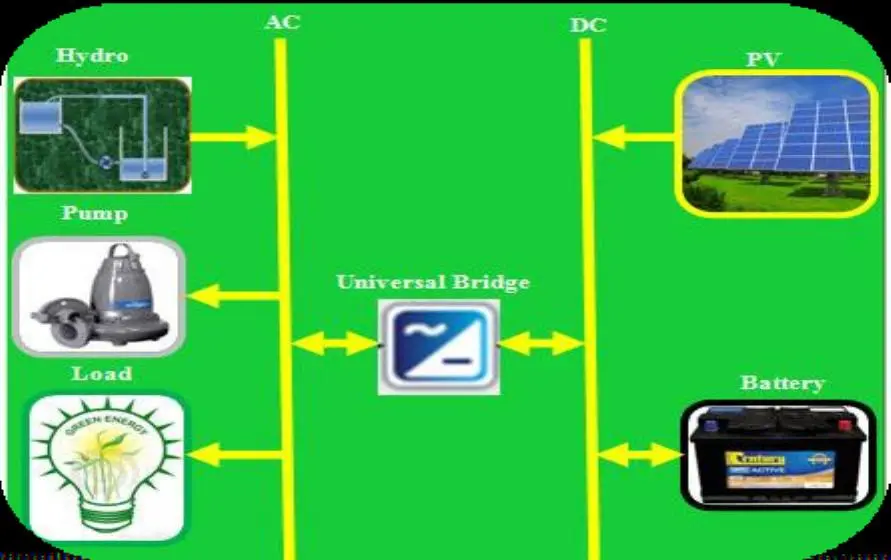
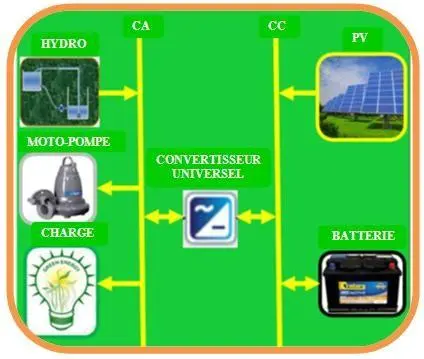
Figure III. 1: Configuration du MSHPEE
SYSTEME HYDRAULIQUE
Une centrale hydroélectrique a essentiellement deux principales parties : la partie mécanique (turbine hydraulique, conduite forcée de turbinage, contrôleur, servomoteur hydraulique, vanne de commande, etc) et la partie électrique (générateur et charge).
La combinaison de la turbine hydraulique, du contrôleur et du servomoteur hydraulique est appelée régulateur de la turbine hydroélectrique.
Le schéma bloc de la figure III.1 ci-dessous illustre une centrale hydroélectrique
[112].
Réglage de la fréquence
Vitesse gouvernant le système
Puissance de sortie














Puissance de référence
Régulateur
Contrôle du
mécanisme
Vanne
Turbine Générateur
Fréquence générée
Transducteur de puissance
Transducteur de fréquence
Figure III. 2: Diagramme fonctionnel d’un système hydraulique
Régulateur de la turbine hydraulique
Le régulateur de la turbine est utilisé pour maintenir une vitesse de turbinage constante en adaptant la fréquence générée et la puissance active en réponse à la variation de la charge lors du fonctionnement. Il régule l’entrée de l’eau dans une turbine qui, à son tour, fait tourner l’alternateur pour générer l’électricité.
Model mathématique du régulateur de la turbine
Les systèmes de régulation des turbines hydrauliques sont fortement influencés par les effets de l’inertie de l’eau et pour régler l’ouverture du clapet, le servomoteur est activé par les signaux générés par le régulateur de la turbine pour contrôler l’électrovanne. L’équation (III.01) ci-dessous est dérivée en fonction de l’hypothèse d’une conduite forcée courte, d’un marteau d’eau insignifiant et d’un écoulement incompressible du fluide dans la conduite forcée du turbinage. Elle définit les caractéristiques du flux de la turbine par unité en termes de constante de temps de l’eau et de la hauteur [112].
= (−H−∑ ) (III.01)
Avec q : le débit de la turbine, HS : la hauteur statique de la colonne d’eau, H : à l’entrée de la turbine, ∑ : les pertes de charge dans la conduite forcée de turbinage, Lc : la longueur de la section la conduite forcée de turbinage et A : la section transversale de la conduite forcée.
Les fonctions du débit et du moment de la turbine CrossFlow sont données par :
Q = Q(H, x, y) et Mt = Mt(H, x, y) (III.02)
Lorsque les paramètres de la turbine varient faiblement à un état d’opération stable, les
équations ci-dessous peuvent être linéarisées comme suit :
q = eqyy + eqxx + eqhh et Mt = eyy + exx + ehh (III.03)
Modélisation du régulateur de la turbine
Le régulateur PID (proportional : dépend de l’erreur actuelle, integrator : accumulation d’erreurs passées and derivative : prédiction des erreurs futures, en fonction du taux de variation actuel) est utilisé comme le contrôleur et l’erreur de la vitesse comme son entrée. Il doit réduire la différence entre la vitesse réelle et la vitesse de référence en ajustant les constantes [111] [112] [118].
Le signal de sortie du régulateur PID peut être écrit en fonction du signal d’erreur :
Θ(t) = k e(t) + k ∫ ( )dt + k ( ) (III.04)
p i d
En prenant la transformée de Laplace de l’équation ci-dessus qui est la sortie du PID, nous aurons :
Θ(s) = k E(s) + k ( ) k sE(s)
d i + d
(III.05)
La fonction de transfert du régulateur PID est:
C(s) = ( ) = k + + k s (III.06)
( ) p d
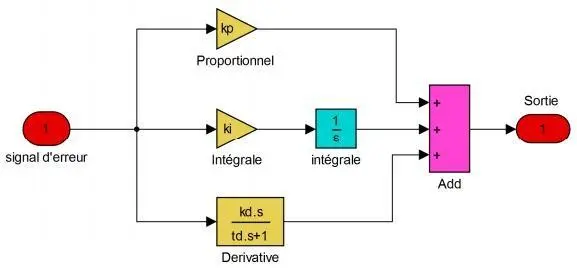
Figure III. 3: Modèle simulink du régulateur
Modélisation du servo-moteur hydroélectrique
Dans le modèle du régulateur de la turbine hydraulique, on contrôle l’électrovanne à partir du signal du contrôleur. Le contrôleur annule l’erreur du signal de la vitesse en envoyant un signal au servomoteur pour contrôler l’électrovanne.
Le couple du moteur est fonction de la vitesse et de l’erreur du signal :
Tm = f ( , e) (III.07)
̇
En utilisant les séries de Taylor, on peut expliquer l’équation précédente comme
suit :
Tm = (ta(0) + (e(t) − e(0)) + … + ( (t) − (0) )+ … µ (III.08)
̇
̇
En négligeant l’ordre des termes les plus élevés et en considérant la condition
initiale zéro, l’équation ci-dessus devient :
Tm = ke(t) − f (t) avec ke= et f=
̇
(III.09)
On sait que la relation mathématique pour un moteur vaut : Tm =J + B (III.10)
̈
̇
où J et B sont respectivement le coefficient de frottement et le moment d’inertie.
En appliquant la transformée de Laplace sur cette égalité, on a :
(III.09)=(III.10) → ( )=
( )
( )
= avec Ka=
et ta=
(III.11)
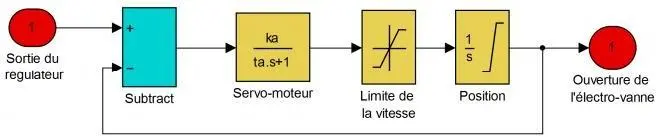 où Ka et ta sont respectivement le gain et la constante de temps.
où Ka et ta sont respectivement le gain et la constante de temps.
(
)
( )
( )
Figure III. 4: Diagramme du servo-moteur hydroélectrique
Modélisation de la turbine hydraulique
Cette section traite des équations décrivant la variation de flux et la puissance mécanique développée en respect de la vitesse de la turbine, de l’ouverture de l’électrovanne et du déplacement des pâles de la turbine hydraulique. Mais, comme la puissance développée par la turbine varie avec le débit, le système fonctionne ou gagne l’état stable lorsque l’écoulement à travers la conduite forcée de turbinage est constant. Les équations liées à la
performance transitoire des turbines hydrauliques sont basées sur les hypothèses suivantes
[112]:
La lame de la turbine est considérée comme lisse (résistance de frottement négligée) ;
Le marteau d’eau sur la conduite forcée est négligé ; Le fluide est considéré comme incompressible ;
La vitesse de l’eau dans la conduite forcée varie directement avec l’ouverture de
l’électrovanne ;
La puissance de sortie développée de la turbine est proportionnelle au produit de la tête et de la vitesse d’écoulement ;
L’équation ci-dessous représente le débit et la puissance mécanique développée à l’arbre respectivement en termes d’ouverture de grille du système et de tête de réseau.
Qt = G (III.11)
Avec G : ouverture de l’électrovanne en rad
Pm = At Hn (Qt – QSC) où At = (III.12)
Avec At: le gain de la turbine, g et g : pleine et sans charge à l’ouverture de l’électrovanne en pu.
Vt = KuG (III.13)
Avec Ku : constante proportionnelle.
L’accélération de l’eau dans la conduite forcée de turbinage est :
= − ( − ) (III.14)
= (III.15)
Avec L : longueur de la conduite forcée de turbinage.
La puissance mécanique est donnée par :
Pm = P – Ppertes où Ppertes = VtSC Hn (III.16)
La figure III.5 ci-dessous illustre le modèle d’une turbine hydraulique.
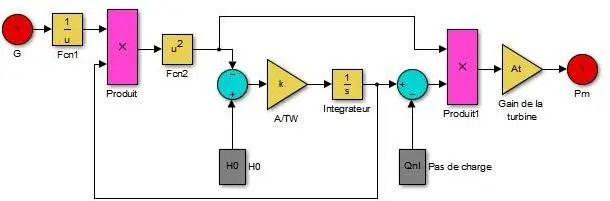
Figure III. 5: Modèle de la turbine hydraulique
Modélisation du régulateur de la turbine hydraulique
Le régulateur de la turbine hydraulique est une partie importante du système hydroélectrique car, il est fondamentalement utilisé à deux fins : premièrement, il permet de développer une puissance mécanique sur l’arbre du génératrice pour produire l’électricité et deuxièmement, il contrôle la variation de la vitesse du génératrice de telle sorte que la fréquence générée demeure constante [112].
Le régulateur PID et le servo-moteur hydroélectrique sont les composants principaux du régulateur de la turbine hydraulique. La modélisation mathématique et la formation de blocs ont été précédemment faites et les modèles de blocs de composants sont connectés de telle sorte que la fréquence générée demeure constante. Le modèle du régulateur de la turbine hydraulique est illustré à la figure III.6.
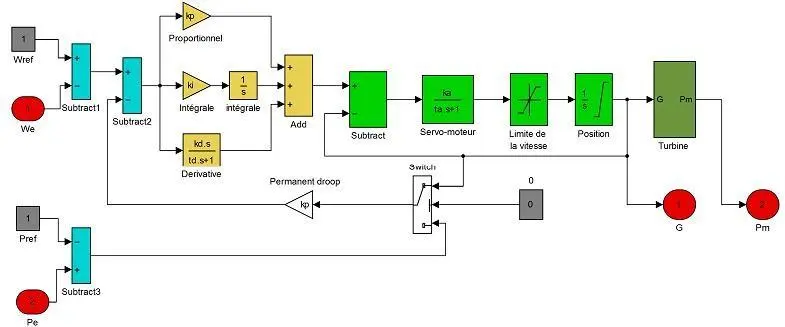
Figure III. 6: Modèle du régulateur de la turbine hydraulique
Modélisation du générateur synchrone
Le modèle mathématique d’un générateur synchrone utilise les équations généralisées de Park. Les équations (III.17) et (III.18) sont utilisées pour modéliser un générateur synchrone [112].
= q − q + ( − ) (III.17)
= d − d + − (III.18)
= f − q + ( − ) (III.19)
= − d − q + − (III.20)
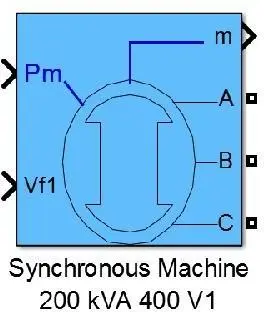 Le modèle de la génératrice synchrone prend en compte la dynamique du stator, du champ et de l’amortisseur des enroulements (voir figure III.7).
Le modèle de la génératrice synchrone prend en compte la dynamique du stator, du champ et de l’amortisseur des enroulements (voir figure III.7).
Pm : puissance mécanique pour le bloc de la machine synchrone (pu)
Vf1 : tension de référence (pu)
m : vecteur contenant les signaux à mesurer A, B et C : sorties de la machine synchrone
Figure III. 7: Modèle de la génératrice synchrone
________________________
2 Définition donnée par l’article 62 de la loi sur les nouvelles régulations économiques (NRE) du 15 mai 2001. ↑
3 Auchan Les 4 Temps, La Défense. ↑
Questions Fréquemment Posées
Quel est le rôle du système hydraulique dans le MSHPEE?
Le système hydraulique dans le MSHPEE est constitué d’une centrale hydroélectrique qui comprend des parties mécaniques et électriques, permettant de réguler l’entrée de l’eau dans une turbine pour générer de l’électricité.
Comment le MSHPEE assure-t-il un approvisionnement ininterrompu en électricité?
Le MSHPEE combine un système solaire principal et un système hydraulique de secours avec un système de stockage d’énergie électrique pour garantir un approvisionnement ininterrompu en électricité.
Quels outils numériques sont utilisés pour la modélisation et la simulation du MSHPEE?
La modélisation et la simulation du MSHPEE sont réalisées sous l’environnement MATLAB/SIMULINK, qui est un outil virtuel de l’ingénierie.
