Les performances de la MASDE révèlent des résultats surprenants dans l’entraînement des machines électriques de forte puissance. Cette étude innovante sur la modulation vectorielle et les stratégies de commande promet de transformer notre compréhension des systèmes multiphasiques, avec des implications cruciales pour l’industrie.
Chapitre I
Modelisation et Commande Vectorielle de la Machine Asynchrone Double Etoile
Introduction
Dans ce chapitre, nous présentons la machine asynchrone double étoile (MASDE) comme la plus courante des machines multipahsées, sans doute parce qu’elle constitue un bon compromis entre une segmentation de puissance suffisante et un ensemble convertisseur- machine pas trop compliqué [HAD 01].
L’étude n’est pas facile car les équations de la MASDE sont très complexes, vu que les coefficients sont des fonctions périodiques du temps. L’élimination du problème des coefficients variables nécessite la transformation de Park qui transforme le système d’équations à coefficients variables à un système d’équations à coefficients constants, ceci facilite la mise en œuvre de la simulation.

La commande des machines asynchrones a beaucoup évolué en particulier dans la commande vectorielle par orientation du flux et ceci grâce au développement de l’électronique de puissance et de la micro-informatique. Cette méthode de commande permet de concevoir des variateurs de vitesse robustes dont le comportement dynamique est semblable à celui des machines à courant continu.
Au cours de ce chapitre, nous présentons une simulation numérique de l’application de la commande indirecte avec et sans régulation de la vitesse.
Mise en Equations
Préliminaires
Description, rappels
La MASDE se compose de deux enroulements triphasés identiques, les deux étoiles se partagent le même stator et sont décalés d’un angle électrique 30° [CHE 98]. Ces enroulements ont le même nombre de pôles et sont alimentés à la même fréquence.
La structure du rotor reste identique à celle d’une machine triphasée, elle peut donc être bobiné soit à cage d’écureuil. Pour simplifier, nous considérerons que les circuits électriques du rotor sont équivalents à un enroulement triphasé en court-circuit [HAD 01] [ROG 03].
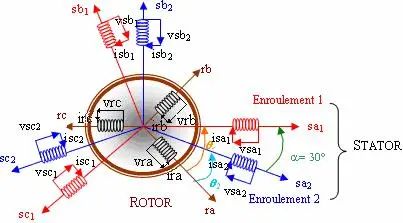
Fig. I.1. Différents enroulements de la MASDE
L’angle r exprime la position du rotor (phase ra) par rapport au stator 1(phase sa1), et 2 la position du rotor par rapport au stator 2(phase sa2) :
r r t 0
r 2
Avec r la vitesse mécanique du rotor.
[I.1]
[I.2]
Si s est la pulsation fondamentale des courants statoriques, la vitesse de rotation de la force
magnétomotrice (f.m.m) d’entrefer est s
s / p
(vitesse de synchronisme), p étant
le nombre de paires de pôles de la machine. La vitesse de rotor vaut :
s
p
r 1 g
[I.3]
Où g est le glissement relatif au fondamental de la f.m.m :
g s p s
r [I.4]
La pulsation des courants rotoriques fondamentaux est alors :
r g s [I.5]
Hypothèses simplificatrices
La modélisation s’appuie sur un certain nombre d’hypothèses [HAD 01] :
Parfaite symétrie de construction ;
Absence de saturation du circuit magnétique ;
Les valeurs des inductances propres et mutuelles sont indépendantes des intensités des courants ;
Les variations des résistances des enroulements en fonction de la température sont négligées ;
Les pertes dans le fer ne sont pas prises en compte dans la mise en équation de la machine.
Répartition sinusoïdale le long de l’entrefer, et des champs magnétiques de chaque bobinage ;
Nous admettrons que les deux enroulements triphasés statoriques sont équilibrés. Finalement, les équations des circuits électriques font intervenir des inductances propres et mutuelles permettant de définir les flux en fonction des courants. Elles se présentent naturellement sous forme matricielle.
- Modèle dans le repère naturel (sa1-sb1-sc1) (sa2-sb2-sc2)- (ra-rb-rc)
Nous travaillons avec une notation matricielle. Pour cela, nous utilisons les vecteurs de variables suivants :
Vecteurs de tension, courant et flux des deux enroulements du stator
[vs ]
[is ]
[vsa1
[isa1
vsb1
isb1
vsc1
isc1
vsa 2
isa 2
vsb 2
isb 2
t
sc 2
v ]
t
i ]
sc 2
[I.6]
[I.7]
[s ]
[sa1
sb1
sc1
sa 2
sb2
t
sc 2
]
[I.8]
Vecteurs de tension, courant et flux du rotor
[vr ]
[ir ]
[vra [ira
vrb rc
irb rc
v ]
i ]
t
t
[I.9]
[I.10]
[r ]
[ra
t
rb rc
]
[I.11]
Equation aux tensions
La loi d’Ohm combinée à la loi de Lenz permet d’écrire la relation suivante en convention récepteur, valable quel que soit le fonctionnement [HAD 01] [RAZ 03]:
[vs ]
[vr ]
* [is ]
[ir ]
[Rs ] [0]6 3
[0]3 6 [Rr ]
[ s ]
[r ]
d
dt
[I.12]
avec [0]63 la matrice nulle de dimension (nX m).
[Rs ] et [Rr ] sont les matrices des résistances statoriques et rotoriques :
[1]n
la matrice identité d’ordre n
[Rs ]
[Rr ]
R[1]6
R[1]3
[I.13]
[I.14]
Equation aux flux
Les équations des flux en fonction des courants sont :
[ s ]
* [is ]
[I.15]
[r ] [ir ]
[Lss ] [M sr ]
[M
sr
]t
[L ]
rr
Les sous- matrices des équations aux flux sont : La matrice des inductances statoriques :
Lls1 Ms
Ms cos(2
/ 3)
Ms cos(4
/ 3)
Pour enroulement 1 :
Ls1 s1
Ms cos(4
/ 3)
Lls1 Ms
Ms cos(2
/ 3)
[I.16]
Ms cos(2
/ 3)
Ms cos(4
/ 3)
Lls1 Ms
Lls 2 M s
M s cos(2
/ 3)
M s cos(4
/ 3)
Pour enroulement 2 :
Ls 2 s 2
M s cos(4
/ 3)
Lls 2 M s
M s cos(2
/ 3)
[I.17]
M s cos(2
/ 3)
M s cos(4
/ 3)
Lls 2 M s
La matrice des inductances rotoriques
Lr.r :
Llr Mr
Mr cos(2
/ 3)
Mr cos(4
/ 3)
Lr r
Mr cos(4
/ 3)
Llr Mr
Mr cos(2
/ 3)
[I.18]
Mr cos(2
/ 3)
Mr cos(4
/ 3)
Llr Mr
avec Lls1, Lls2 : les inductances propres de fuite des deux enroulements statoriques.
Llr : inductance de fuite rotorique.
Ms : inductance mutuelle de magnétisation statorique.
Mr : inductance mutuelle de magnétisation rotorique.
Nous établissons la matrice des inductances mutuelles Stator 1-Stator 2 matrice des inductances mutuelles Stator 2-Stator 1 [M s 2 s1 ] :
[Ms1 s 2 ] , et la
cos( )
cos(
– 2/3)
cos(
2/3)
[M s1 s2 ]
t
s2 s1
[M ]
M s cos(
2/3)
cos( )
cos(
– 2/3)
[I.19]
cos(
– 2/3)
cos(
2/3)
cos( )
La matrice des inductances mutuelles Stator 1-Rotor [M s1 r ] , et la matrice des inductances mutuelles Rotor- Stator 1 [M r s1 ] :
cos( p r )
cos( p
r – 2
/3)
cos( p r
2/3)
[M s1 r ]
t
r s1
[M ]
M sr
cos( p r
2/3)
cos( p r )
cos( p
r – 2
/3)
[I.20]
cos( p
r – 2
/3)
cos( p r
2/3)
cos( p r )
La matrice des inductances mutuelles Stator 2-Rotor [M s 2 r ] , et la matrice des inductances mutuelles Rotor- Stator 2 [M r s2 ] :
cos( p r – )
cos( p
r – 2
/3 – )
cos( p r
2/3 – )
[M s 2 r ]
t
r s2
[M ]
M sr
cos( p r
2/3 – )
cos( p r – )
cos( p
r – 2
/3 – )
[I.21]
cos( p
r – 2
/3 – )
cos( p r
2/3 – )
cos( p r – )
avec Msr : mutuelle inductances statorique et rotorique.
Equation mécanique
L’équation mécanique instantanée classique s’exprime en fonction de l’inertie J des parties
tournantes, du coefficient de frottement fr et de couple de charge Cr tel que :
J dr
dt
Cem Cr
f r r
[I.22]
Couple électromagnétique
D’après les lois de l’électromagnétisme classique, le couple sur l’arbre s’exprime en fonction des courants et de la dérivée par rapport à t de la matrice inductance globale :
Cem
[is abc1 ]
p
2
t
d [L dt
s1 r
][i
r abc ]
[is abc 2 ]
t
d [L dt
s 2 r
][i
r abc ]
[I.23]
Transformation de Park
Pour résoudre le problème posé par la dépendance des inductances de l’angle de rotation, une grande simplification peut être obtenue par transformation du système d’équations précédent tout en gardant le principe de la conservation de la puissance et des forces magnétomotrices.
De ce fait, nous substituons les enroulements statoriques par un enroulement biphasé équivalent. La transformation de Park consiste à transformer le système (a1, b1, c1, a2, b2, c2) triphasé en un système (d, q) biphasé en quadrature.
Nous définissons la matrice de Park par :
P()
A(s1 ) 0
[I.24]
0 A(
s2 )
Pour le premier enroulement du stator, nous avons :
A(s1 )
2 / 3
cos( sin( 1/
s1 )
s1 )
2
cos(s1
sin(s1
1/
2
2 / 3)
2 / 3)
cos( sin(
s1 s1
1/
2
2 / 3)
2 / 3)
[I.25]
Pour le deuxième enroulement du stator :
A(s 2 )
2 / 3
cos( sin( 1/
s 2 )
s 2 )
2
cos(s 2
sin(s 2
1/
2
2 / 3)
2 / 3)
cos( sin(
s 2
s 2
1/
2
2 / 3)
2 / 3)
[I.26]
Tel que :
s 2 s1
[I.27]
Pour le rotor :
cos(s1 | r ) | cos( | s1 | r | 2 | / 3) | cos( | s1 | r | 2 / 3) | |||
P(r ) | 2 / 3 | sin(s1 | r ) | sin( | s1 | r | 2 | / 3) | sin( | s1 | r 2 / 3) | [I.28] | |
1/ 2 | 1/ | 2 | 1/ | 2 |
avec :
P(s ) : matrice de transformation de park du stator
A(s1 )
A(s 2 )
: matrice de transformation de park du premier enroulement statorique
: matrice de transformation de park deuxième enroulement statorique
P(r ) : matrice de transformation de park de l’enroulement rotorique
Les courants, flux et tensions s’écrivent de la manière suivante :
[is,dq1] = [A( s1)] [is,ab1] [ s,dq1] = [A( s1)] [ s,abc1] [vs,dq1] = [A( s1)] [vs,abc1]
[is,dq2] = [A( s2)] [is,abc2] , [ s,dq2] = [A( s2)] [ s,abc2] , [vs,dq2] = [A( s2)] [vs,abc2] [ir,dq] = [P( r)] [ir,abc] [ r,dq] = [P( r)] [ r,ab2]
Choix du référentiel
Le modèle de la machine asynchrone a été présenté dans un repère « d, q » dont l’orientation reste quelconque. Cependant, selon les caractéristiques et les objectifs de l’application, il est plus commode de fixer l’orientation du repère de façon adéquate afin de faire apparaître certaines grandeurs dont nous désirons plus particulièrement suivre l’évolution.
Ainsi, trois possibilités peuvent être adoptées : Référentiel lié au stator ;
Référentiel lié au rotor ;
Référentiel lié au champ tournant ;
Nous adaptons ce dernier repère tel que : ( d s1 , d s 2 et ).
dt s
dt s gl s r
Il est utilisé dans les applications d’alimentation des machines asynchrones par convertisseur de fréquence.
Cependant, il sera utilisé pour notre modèle.
Après multiplication des matrices et transformations trigonométriques, les équations des tensions de la machine peuvent être représentées sous la forme suivante :
vs1d vs 2d vs1q
v
Rsis1d dt
Rsis 2d dt
d
s1d
d
s 2d
d
s1q
Rsis1q dt R i
d
s 2q
s s1q
s s 2q
s s1d
[I.30]
s 2q
0 R i
s s 2q dt
d rd
s s 2d
r rd dt
d
rq
- Rr irq dt
gl rq
gl rd
avec : gl
d gl
s r dt
: Vitesse de glissement.
Les relations entre flux et courants sont données par :
f s1d f s 2d f s1q
Ls1is1d Ls 2is 2d
Ls1is1q
Mc (is1d Mc (is1d Mc (is1q
is 2d
is 2d
is 2q
ird ) ird ) irq )
f s 2q
Ls 2is 2q
Mc (i
s1q
is 2q
irq )
[I.31]
f rd
f rq
Lcrird Lcr irq
Mc (is1d
Mc (is1q
is 2d
is 2q
ird )
irq )
Sachant que :
Mc =3/2 Mrs= 3/2 Msr : Inductance mutuelle entre Rotor et le premier enroulement du Stator ou le deuxième enroulement du Stator.
Ls1 Lcr
Ls 2
Llr
Lls Mc
Mc : Inductance de fuite statorique.
: Inductance de fuite rotorique.
Le couple électromagnétique développé par la machine est donné par l’expression :
Mc
Lcr
Cem
p
rd ( i
s1q
is 2q )
rq ( i
s1d
is 2d )
[I.32]
Mise sous forme d’équations d’état
Il y a plusieurs manières d’écrire les équations d’état du système défini précédemment.
t
]
Nous choisissons dans ce qui suit, le vecteur [is1d is 2d is1q is 2q rd comme
rq
vecteur d’état et les grandeurs vs1d , vs 2d , vs1q , vs 2q comme variables de commande. Ainsi, nous
exprimons [s1d s 2d s1q s 2q ird irq ] en fonction du vecteur choisi, d’où :
ird
(Lcr
rd
Mc
Mc )
(Lcr
Mc )
( is1d
is 2d )
[I.33]
i rq Mc ( i i )
rq
s1q s 2q
(Lcr Mc ) (Lcr Mc )
Nous avons alors :
s1d
(L | M ) | is |
(L | M ) | is |
(L | M ) | is |
(L | M ) | is |
ls c 1d
Mcllr
L M
Mc
is 2d rd
Llr
Mc
s 2d
ls c 2d
lr
M cllr
L M
c
M c
is1d rd
Llr
Mc
s1q
ls c 1q
lr
M cllr
L M
c
Mc
is 2q L M rq
[I.34]
lr c
M cllr i
lr c
Mc
Llr
M c
s 2q
ls c 2q
Llr M c
s1q
rq
De même, la matrice des tensions est écrite de la manière suivante :
Nous posons :
Rsm
2
Rs c
M
; M ‘
M 2
M c c
L
Lcr r cr
c
2
Rsm
c
Lcr r
sLcs
M2
s c
M‘
Mc
r
0
M
c
Lcrr
sLcs
‘
‘ Mc s c
cr r
M
L
M
Mc
r
L
cr
M
d
M
i
0
0
vs1d vs2d
Rsm
M‘
sMc
R
sLcs
2
M
c
c
Lcrr
Mc
c
r s1d
L
cr
i
Mc s2d
s2q | 0 | 0 | M‘ | L | 0 | 0 | dt is2q |
rd | 0 | 0 | 0 | 0 | 1 | 0 | rd |
rq | 0 | 0 | 0 | 0 | 0 | 1 | rq |
Lcs
‘
M
c
‘
c
Lcs 0 0
0 0
0 0
is1d is2d
vs1q vs2q
s c sm
2
M
L c
Lcr r
R
L
r
cr
L
Mc
Lcrr
Mc
is1q i
- 0 Lcs c 0
c cs
M
‘
0
is1q
0
0
s cs
Mc
r
0
Lcr r
0
Mc
r
cr cs c
1
r gl
cr r cs c
gl
1
r
( Lcs ) ‘ 0 0
M
c
( Lcs2
c
c
2 M ‘ 2 )
( Lcs2
2 M ‘ 2 )
M ‘ ( L )
c cs 0 0
c
c
( Lcs 22
M
c
B 0
M ‘ 2 )
( Lcs2
2 M ‘ 2 )
0
( Lcs ) ‘
c
c
( Lcs2
0 0 | 0 0 | M ‘ ( L 2 2 M ‘ 2 ) 0 | ( Lcs ) ( L 2 2 M ‘ 2 ) cs c 0 |
0 | 0 | 0 | 0 |
2 M ‘ 2 )
( Lcs2
2 M ‘ 2 )
c
cs c
________________________
2 Définition donnée par l’article 62 de la loi sur les nouvelles régulations économiques (NRE) du 15 mai 2001. ↑
3 Auchan Les 4 Temps, La Défense. ↑
Questions Fréquemment Posées
Qu’est-ce que la machine asynchrone double étoile (MASDE) ?
La machine asynchrone double étoile (MASDE) est une machine multiphasée courante, constituant un bon compromis entre une segmentation de puissance suffisante et un ensemble convertisseur-machine pas trop compliqué.
Comment fonctionne la commande vectorielle de la MASDE ?
La commande des machines asynchrones a beaucoup évolué, en particulier grâce à la commande vectorielle par orientation du flux, permettant de concevoir des variateurs de vitesse robustes dont le comportement dynamique est semblable à celui des machines à courant continu.
Quelles sont les hypothèses de modélisation pour la MASDE ?
Les hypothèses de modélisation incluent la parfaite symétrie de construction, l’absence de saturation du circuit magnétique, et que les valeurs des inductances sont indépendantes des intensités des courants.