Les meilleures pratiques en flexion électromagnétique révèlent des résultats surprenants sur l’influence du potentiel magnétique sur les contraintes de cisaillement dans les coques à double courbure. Cette étude innovante promet de transformer notre compréhension des matériaux composites, avec des implications significatives pour l’ingénierie moderne.
- Effet du potentiel magnétique sur la variation de la contrainte de cisaillement
yz
- Effet du potentiel magnétique sur la variation de la contrainte de cisaillement
Les Figs.II.22 fournies illustrent la distribution de la contrainte de cisaillement transverse normalisée
yz selon l’épaisseur réduite z/h, pour trois géométries structurelles distinctes — plaque, cylindre et
sphère — en fonction du paramètre de porosité initiale, avec des valeurs fixées de ξ=0.1, p=4, 0 et

0 2,0,2. L’objectif est de mettre en évidence l’influence du potentiel magnétique et de la porosité initiale du matériau fonctionnellement gradué (FGM) sur la réponse en cisaillement transverse dans des configurations géométriques variées.
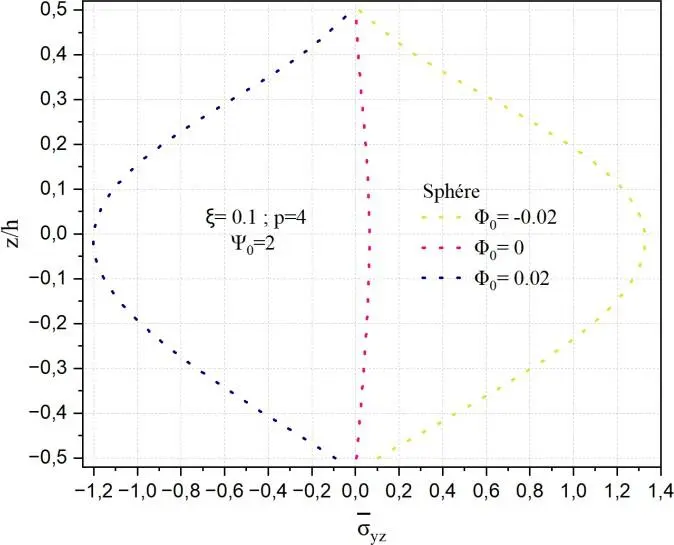
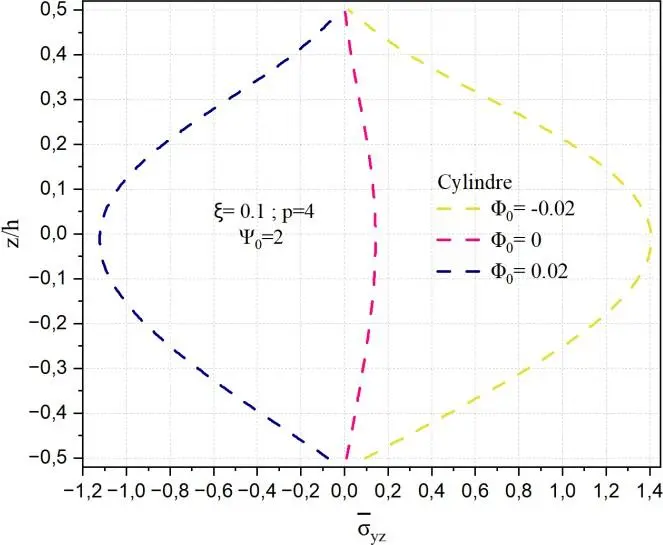
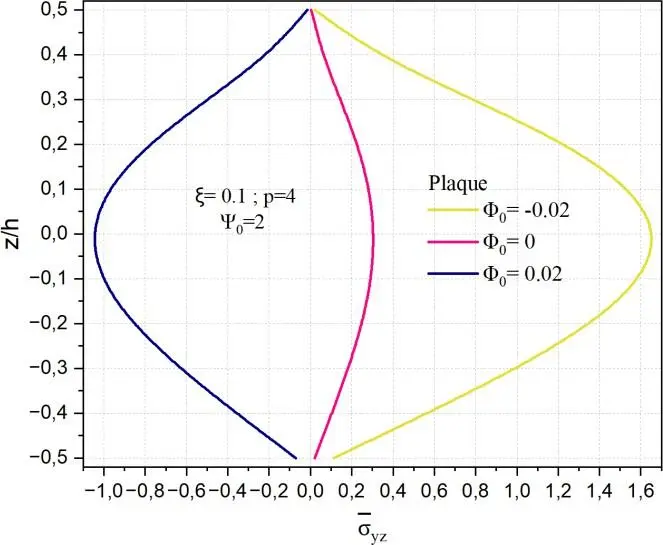
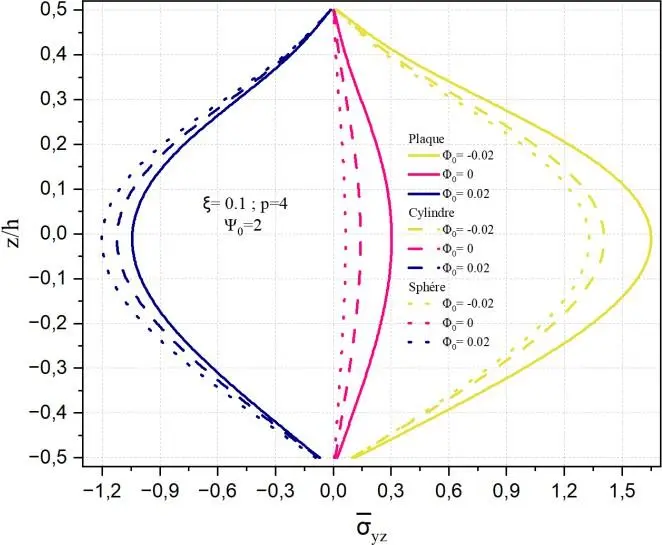
Fig. II.22. Variation de la contrainte de cisaillement transverse yz à travers l’épaisseur de la
coque en FGM pour différentes valeurs de potentiel magnétique 0 .
Pour la plaque, la courbe de xz est fortement influencée par la valeur 0 . Un potentiel magnétique
0 0.02 induit une augmentation significative de la contrainte transverse maximale, atteignant des
valeurs supérieures à 1.4, ce qui traduit une élévation notable de la rigidité effective en cisaillement
dans la zone centrale de la plaque. À l’inverse, une porosité négative ( 0 0.02 ) réduit considérablement cette contrainte, suggérant un matériau plus souple ou endommagé dans les zones
Critiques. La forme symétrique et convexe des courbes indique que le cisaillement est maximal au centre de la plaque et tend vers zéro aux interfaces, conformément au comportement attendu d’un champ de cisaillement transverse sous flexion pure dans des structures symétriques.
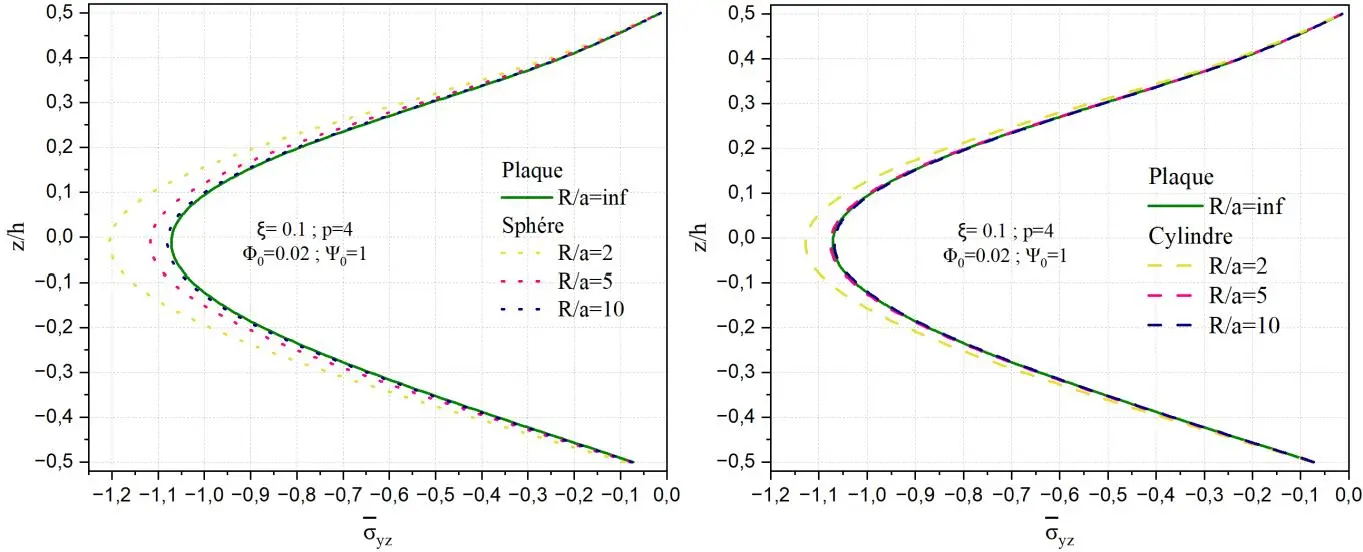
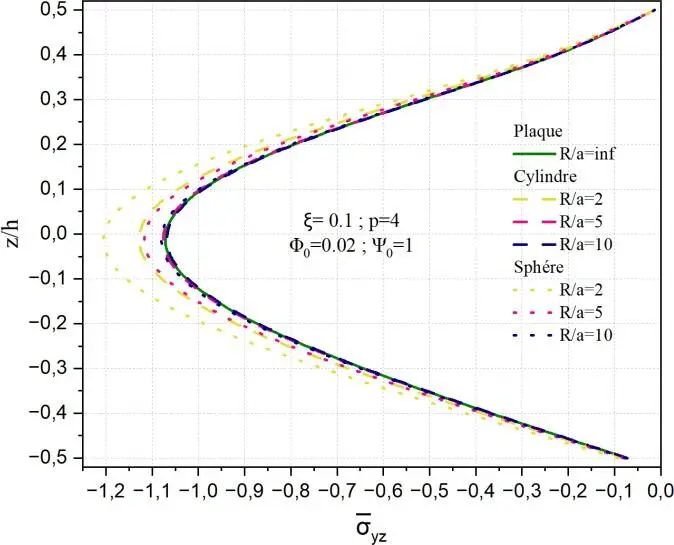
Fig. II.23. Variation de la contrainte de cisaillement transverse yz à travers l’épaisseur de la coque
en FGM pour différents rapports géométriques R/a.
La Fig. II.23 montre la variation de la contrainte de cisaillement transverse normalisée yz à travers
l’épaisseur normalisée z/h d’une plaque FGM soumise à des champs électrique et magnétique, avec
une porosité ξ=0.1, un indice de gradation p=4, un potentiel électrique 0 1 et un potentiel
magnétique 0 0.02. Deux géométries courbes sont considérées : sphérique et cylindrique,
comparées à une plaque plane (R/a = ∞). Contrairement à la contrainte yz ici la contrainte yz reste
négative sur toute l’épaisseur et présente un profil relativement symétrique, avec un maximum (en valeur absolue) autour de la fibre neutre. On observe que l’effet de la courbure est moins marqué que
pour yz bien que l’influence de la géométrie sphérique soit légèrement plus notable que celle du
cylindre. Pour R/a=2, la contrainte devient plus intense, mais l’écart avec la plaque plane demeure
modéré. Ce comportement suggère que la contrainte yz étant associée au cisaillement transverse,
est moins sensible à la courbure que le cisaillement dans le plan, et principalement influencée par la variation des propriétés mécaniques selon z, induite par le gradient de matériau et la porosité. En
somme, l’effet de la courbure sur yz est présent mais reste secondaire comparé à celui observé pour
yz .
- Effet de la porosité sur l’évolution de la contrainte de cisaillement
xy dans les structures
- Effet de la porosité sur l’évolution de la contrainte de cisaillement
La Fig. II.24 illustre la distribution de la contrainte de cisaillement xy à travers l’épaisseur
normalisée z/h pour trois types de géométries (plaque, cylindre et sphère), en tenant compte de l’effet de la porosité via différents taux ξ en FGM sous l’effet du potentiel électrique et du potentiel magnétique. Dans le cas de la plaque, la variation de xy présente un profil fortement non linéaire
caractéristique des théories de cisaillement d’ordre élevé, avec des valeurs presque nulles à la surface supérieure libre et un maximum bas de la plaque. L’augmentation du taux de porosité entraîne une diminution progressive de l’intensité de la contrainte maximale, traduisant l’effet d’assouplissement induit par la présence de pores dans le FGM. Cet affaiblissement faible est d’autant plus marqué que le matériau présente une configuration plane, où les mécanismes de redistribution des contraintes sont plus sensibles à l’hétérogénéité matérielle. La contrainte minimale se trouve dans la partie supérieure
-0.95 à z/h=0.25.
En revanche, pour les structures cylindriques, la contrainte xy conserve une variation non
linéaire, mais moins accentuée que dans le cas plan. Les courbes correspondant aux différentes porosités restent proches, suggérant que la géométrie incurvée favorise une répartition plus uniforme des efforts transverses, atténuant ainsi l’influence de la porosité. L’effet de la porosité reste perceptible mais modéré, en raison du rôle stabilisateur de la courbure longitudinale qui agit comme une barrière géométrique aux concentrations de contraintes.
Enfin, dans le cas des coques sphériques, la distribution de xy apparaît quasi linéaire, indiquant
un comportement mécanique particulièrement homogène. L’influence de la porosité y est pratiquement négligeable, les courbes étant quasiment superposées pour l’ensemble des valeurs de ξ. Cette insensibilité relative est attribuable à la double courbure intrinsèque de la géométrie sphérique, qui engendre une rigidité accrue et une dissipation efficace des charges transversales dans toutes les directions, réduisant de manière significative les effets localisés induits par la porosité. Les contraintes de cisaillement les plus faibles se trouvent dans la plaque.
Ces résultats soulignent la pertinence de la HSDT pour capturer les effets fins de gradient de cisaillement dans les structures composites poreuses, tout en mettant en évidence le rôle crucial de la géométrie dans la sensibilité mécanique à l’endommagement par porosité. Tandis que les plaques se révèlent vulnérables à l’effet de dégradation, les coques incurvées, notamment sphériques, présentent une robustesse accrue, suggérant leur aptitude à des applications où des performances mécaniques stables sont requises malgré la présence de défauts microstructuraux.
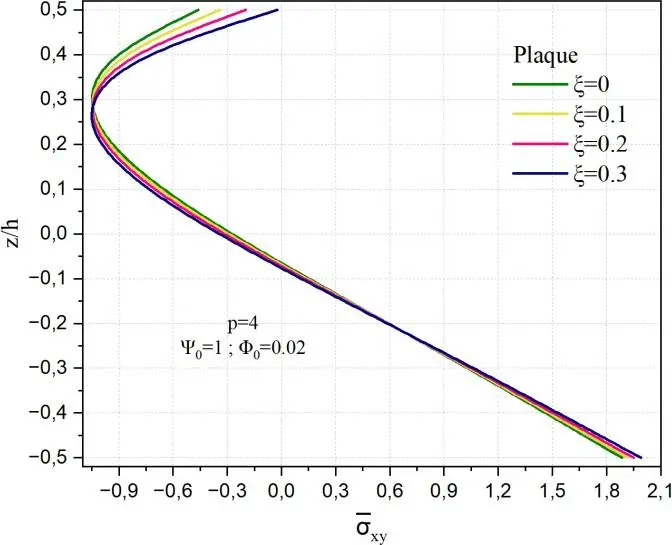
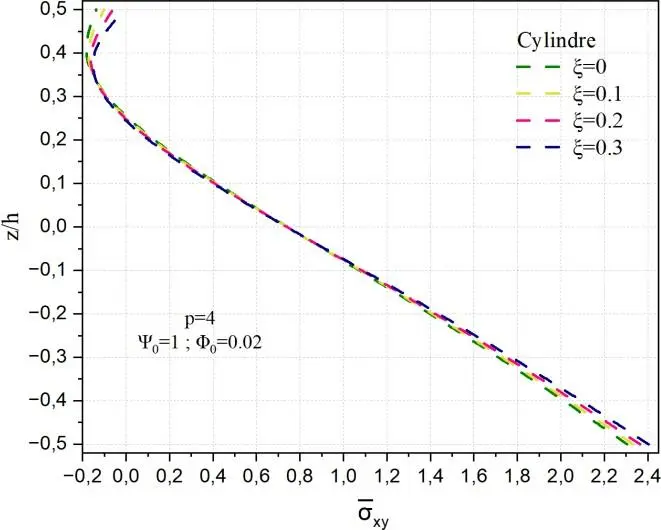
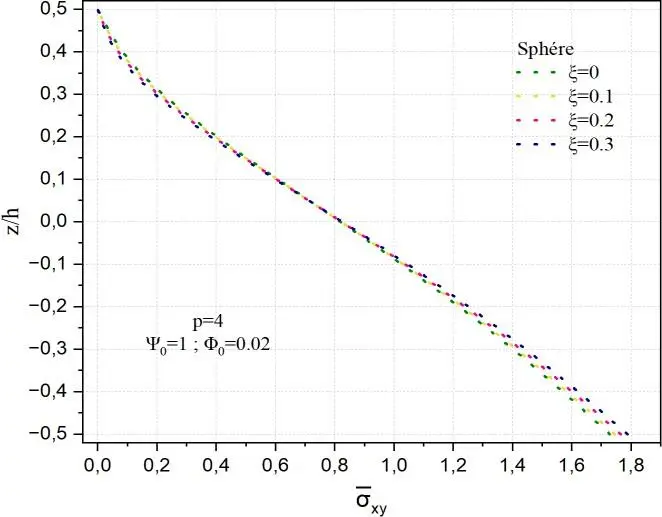
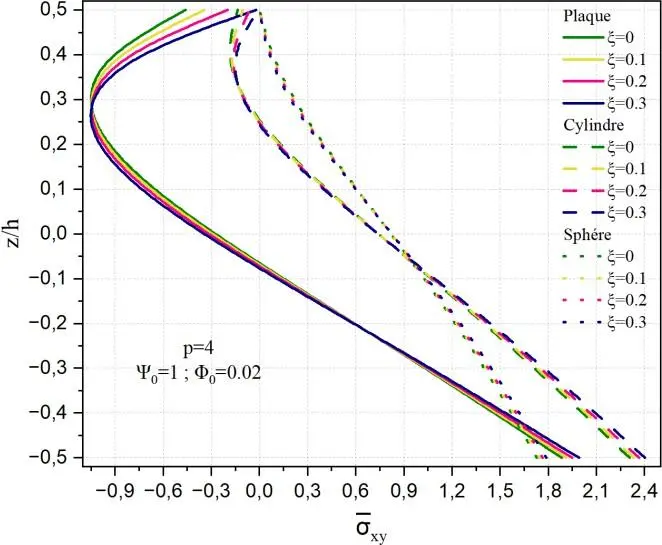
Fig. II.24. Variation de la contrainte xy à travers l’épaisseur d’une coque en FGM pour différentes
valeurs de porosité .
- Effet du potentiel électrique sur la variation de la contrainte de cisaillement
xy
- Effet du potentiel électrique sur la variation de la contrainte de cisaillement
Les Figs. 25 présentées illustrent la distribution de la contrainte de cisaillement transverse normalisée
xy selon l’épaisseur normalisée z/h, pour différentes géométries (sphère, cylindre, plaque) et
diverses valeurs du paramètre de distribution fonctionnelle des matériaux 0 2,0,2, à porosité
constante ξ=0,1. On observe que l’effet de 0 sur la répartition des contraintes est fortement
dépendant de la géométrie : dans le cas de la plaque, l’augmentation de 0 entraîne une nette hausse de la contrainte maximale au centre, traduisant une déplace cette rigidité vers les faces, réduisant ainsi les contraintes internes. Le cylindre montre un comportement intermédiaire, où la variation de xy
reste significative mais moins marquée qu’en plaque. La sphère, quant à elle, présente une répartition quasi linéaire et modérément sensible à 0 , la double courbure contribuant à une répartition plus uniforme des contraintes. Ces résultats confirment que la distribution fonctionnelle du matériau,
couplée à la géométrie de la structure, influence fortement les mécanismes de cisaillement, particulièrement captés par les modèles à haut ordre de cisaillement.
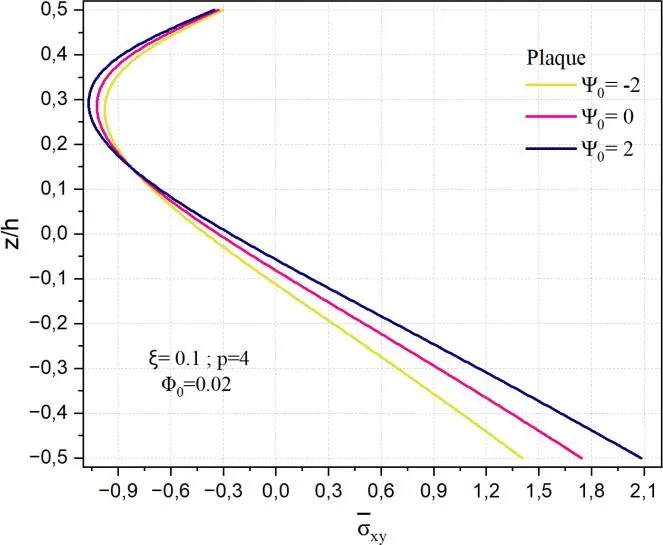
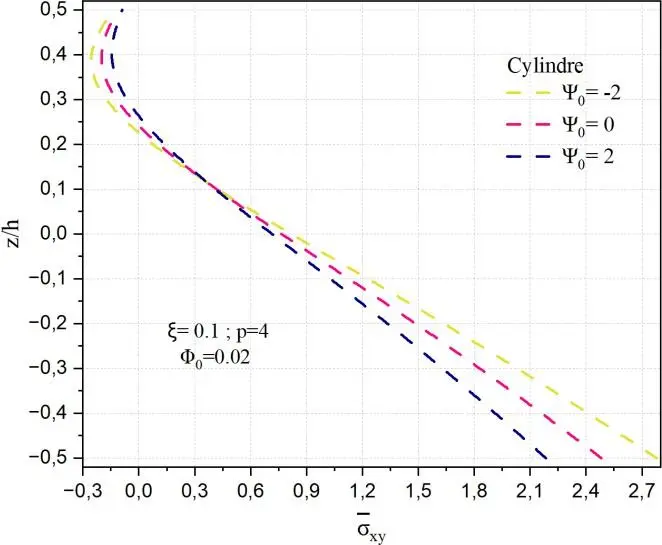
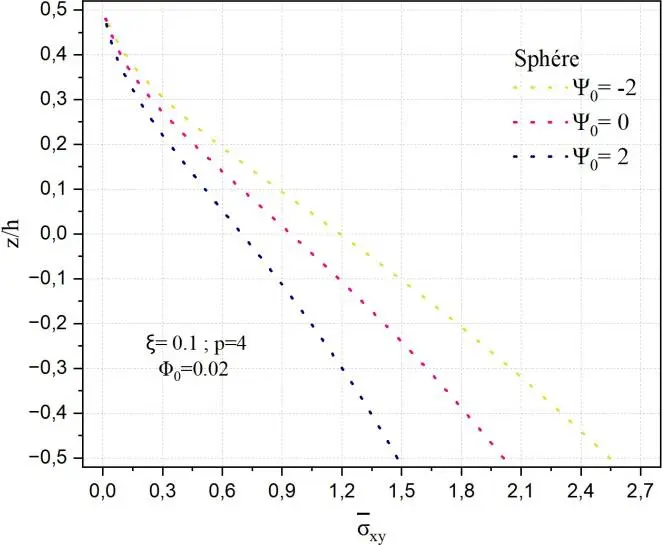
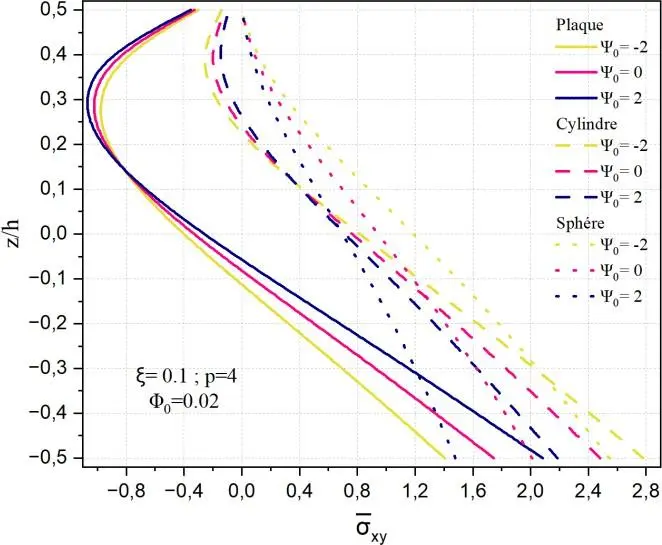
Fig. II.25. Variation de la contrainte xy à travers l’épaisseur d’une coque en FGM pour
différentes valeurs de potentiel électrique 0 .
L’application d’un champ électrique modifie l’état de contrainte interne par l’effet
piézoélectrique inverse : un potentiel électrique positif 0 0 induit des déformations
supplémentaires qui renforcent localement la rigidité électromécanique, augmentant ainsi les contraintes de cisaillement, notamment vers les couches électriquement activées. À l’inverse, un
potentiel négatif 0 0 provoque des déformations de signe opposé, ce qui relâche partiellement
les contraintes dans certaines régions. Cette influence est plus marquée dans les plaques, qui ne disposent pas de courbure géométrique pour redistribuer les effets induits, alors que dans les cylindres et les sphères, la courbure tend à lisser la réponse et à disperser plus largement l’effet du champ électrique.
Questions Fréquemment Posées
Quel est l’effet du potentiel magnétique sur la contrainte de cisaillement transverse dans les coques ?
Un potentiel magnétique induit une augmentation significative de la contrainte transverse maximale, atteignant des valeurs supérieures à 1.4, ce qui traduit une élévation notable de la rigidité effective en cisaillement dans la zone centrale de la plaque.
Comment la porosité influence-t-elle la contrainte de cisaillement dans les structures ?
L’augmentation du taux de porosité entraîne une diminution progressive de l’intensité de la contrainte maximale, traduisant l’effet d’assouplissement induit par la présence de pores dans le matériau fonctionnellement gradué (FGM).
Quelle est la variation de la contrainte de cisaillement transverse selon la géométrie de la coque ?
La contrainte de cisaillement transverse reste négative sur toute l’épaisseur et présente un profil relativement symétrique, avec un maximum autour de la fibre neutre, l’effet de la courbure étant moins marqué que pour d’autres contraintes.