Le comportement des coques FGM révèle des résultats surprenants : une étude récente montre comment la porosité et les champs électromagnétiques influencent la flexion des coques à double courbure. Ces découvertes transforment notre compréhension des matériaux avancés, avec des implications majeures pour l’ingénierie moderne.
Chapitre I
Généralités sur les matériaux
- Introduction
Ce chapitre est dédié à l’étude des différentes théories de modélisation ainsi qu’à la caractérisation des propriétés matérielles des plaques en matériaux à gradient de propriétés (FGM). Comme présenté dans le chapitre 1, l’utilisation croissante des matériaux FGM dans divers secteurs de l’ingénierie s’explique par les avantages qu’ils offrent en termes de performance et de fiabilité.
Leur structure à gradient de propriétés permet d’apporter des solutions technologiques innovantes, en particulier dans des environnements soumis à des conditions de chargement sévères nécessitant des propriétés mécaniques et thermomécaniques élevées. La modélisation précise de ces structures requiert l’utilisation de théories avancées, notamment des théories d’ordre supérieur capables de prendre en compte les effets de cisaillement transverse.
Ainsi, la première partie de ce chapitre sur les différents modèles utilisés pour décrire la distribution spatiale des propriétés des matériaux FGM, en particulier en fonction de la direction de l’épaisseur.
- Loi de mélange en puissance ou propriété matérielle d’une structure P-FGM
La fraction volumique de la FGM correspond à une fonction de loi de puissance :
V (z) z
h
1 p
2
I.1
Où p est le paramètre matériel et h l’épaisseur de la plaque. Après avoir défini la fraction volumique locale V ( z) , les propriétés matérielles d’une P-FGM peuvent être déterminées par la loi du mélange exprimée par l’équation (I.2) [37, 38] :
E(z)
E E z
c m h
1 p
2
Em
E E
c m 2
I.2
0,5
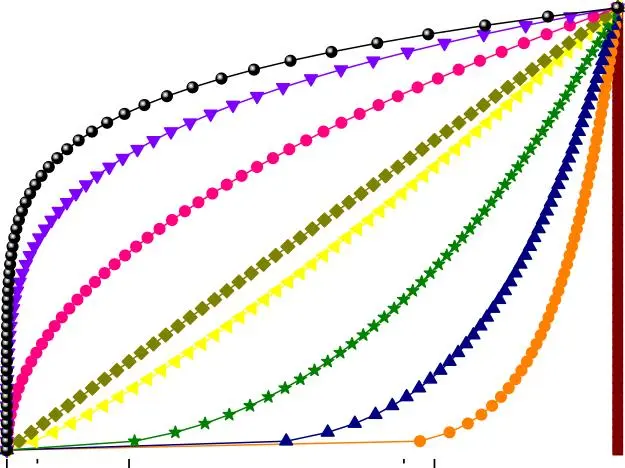
Indice de Puissance
0
0,4
0.1
0.2
0,3
0.4
0.8
1
0,2
2
4
0,1
6
0,0
z/h
-0,1
-0,2
-0,3
-0,4
-0,5
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Vc(z)
Fig. I.1. Variation de la fraction volumique dans une plaque P- FGM.
Où 𝐸𝑚 et 𝐸𝑐 sont respectivement les modules de Young de la surface inférieure (z =h/2) et supérieure (z = h/2) de la plaque de FGM. La variation du module de Young dans le sens de l’épaisseur de la plaque P-FGM est représentée dans la Figure I.1, ce qui montre que le module d’Young change rapidement près de la surface inférieure pour p>1et augmente rapidement près de la surface
supérieure pour p<1 et
(0 ≤
≤ 1) est la fraction volumique de porosité. Les propriétés mécaniques
parfaites de la coque FGM peuvent être obtenues en considérant
= 0.
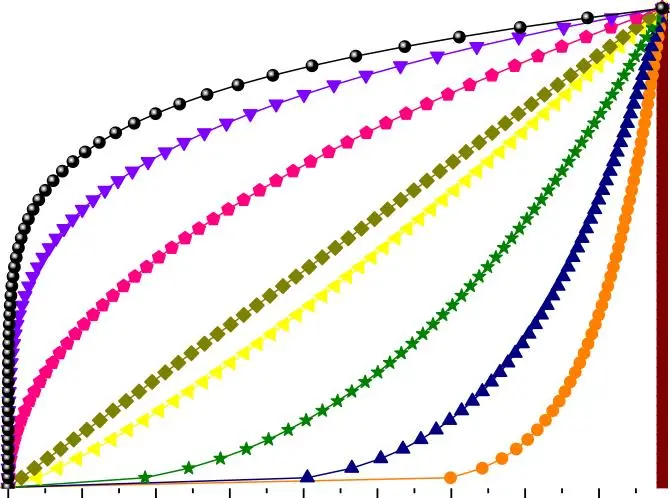
La variation du module de la plaque FGM est montrée sur la Figure I.2.
0,5
0,4
0,3
0,2
0,1
Indice de Puissance
0
0.1
0.2
0.4
0.8
1
2
4
6
0,0
z/h
-0,1
-0,2
-0,3
-0,4
-0,5
70 105 140 175 210 245 280 315 350 385
E(z)
Fig. I.2. Variation du module d’élasticité dans une plaque P- FGM.
0,5
Indice de Puissance
0
0.1
0.2
0.4
0.8
1
2
4
6
0,4
0,3
0,2
0,1
0,0
z/h
-0,1
-0,2
-0,3
-0,4
-0,5
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Vi(z)
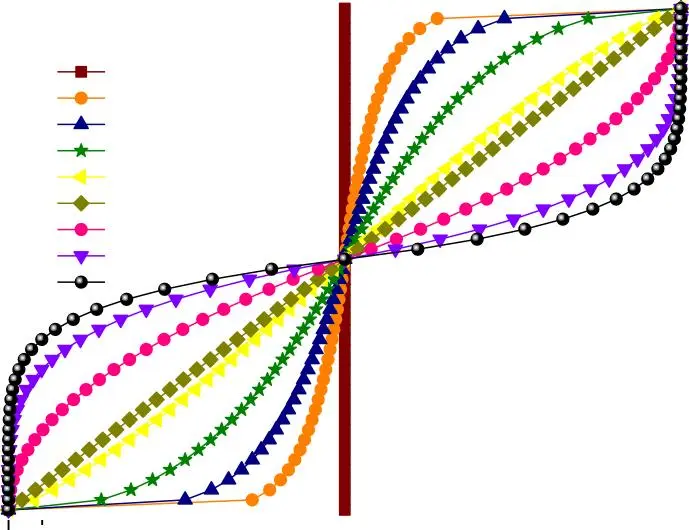
Fig. I.3. Variation de la fraction volumique dans une plaque S- FGM.
- Loi de mélange sigmoïde ou propriété matérielle d’une structure S-FGM
Les variations des propriétés mécaniques et physiques des matériaux à gradient de propriétés (FGM) sont couramment modélisées à l’aide de la loi de puissance, donnant naissance à la classe des P-FGM. Toutefois, dans de nombreux cas, cette distribution engendre des concentrations de contraintes marquées à proximité des interfaces, notamment dans les zones où les propriétés changent rapidement, malgré la continuité du matériau. Pour remédier à cette limitation, Chung et Chi [39] ont introduit un nouveau modèle de distribution, dit S-FGM, basé sur une combinaison de deux fonctions de loi de puissance. Cette approche permet de représenter une transition plus progressive des
propriétés à travers l’épaisseur, réduisant ainsi les pics de contraintes localisés. Les expressions mathématiques définissant cette fraction volumique sigmoïde sont données par les relations I.3 et I.4.
1 h / 2 z p
V1 (z) 2
h / 2
h / 2 z 0
I.3
1 h / 2 z p
V2 (z) 1 2
h / 2
0 z h / 2
I.4
En appliquant la loi du mélange, le module de Young de la FGM-S peut être calculé par :
E1 (z) EcV1 z 1V1 zEm E2 (z) EcV2 z 1V2 zEm
I.5
I.6
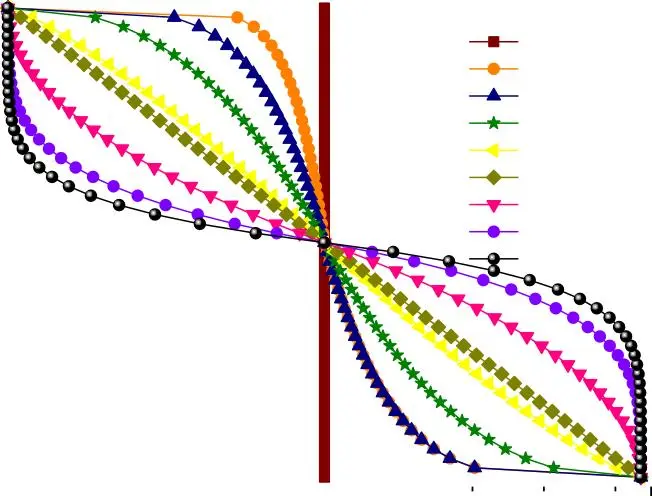
Les Figures I.3 et I.4 présentent la variation de la fraction volumique et le module d’élasticité des répartitions sigmoïdes définie par les équations (I.5) et (I.6). Ainsi, cette plaque FGM est appelée plaque S-FGM.
0,5
Indice de Puissance
0
0.1
0.2
0.4
0.8
1
2
4
6
0,4
0,3
0,2
0,1
0,0
z/h
-0,1
-0,2
-0,3
-0,4
-0,5
70 105 140 175 210 245 280 315 350 385
E(z)
Figure I.4. Variation du module d’élasticité dans une plaque S-FGM.
- Loi de mélange exponentielle ou propriété matérielle d’une structure E-FGM
Cette loi s’emploie en utilisant la fonction exponentielle pour décrire les propriétés matérielles des FGM donnée par la relation I.7.
h
1 Ec
E(z) Em expB z 2 avec
B ln
2 E
I.7
m
La variation du module de Young à travers l’épaisseur des plaques de E-FGM est représentée sur la figure I.5.
0,5
E(z)
0,4
0,3
0,2
0,1
0,0
z/h
-0,1
-0,2
-0,3
-0,4
-0,5
200 250 300 350
E(z)
Fig. I.5. Variation de module de Young dans une plaque E- FGM.
- Phénomène piézoélectrique
Le phénomène de piézoélectricité fut découvert en 1880 à Paris par Pierre Curie et son frère Paul- Jacques Curie, dans certains matériaux cristallins. Le terme « piézo » provient du grec ancien piezein, signifiant « presser ». Ce phénomène se manifeste sous deux formes principales : l’effet piézoélectrique direct (illustré en Figure I.6) et l’effet piézoélectrique inverse (Figure I.7). Il apparaît dans des matériaux cristallins dépourvus de centre de symétrie [40-42].
L’effet direct correspond à la génération de charges électriques à la surface du matériau sous l’effet d’une contrainte mécanique appliquée. Le signe des charges dépend de l’orientation de la contrainte appliquée. Inversement, l’effet piézoélectrique inverse se manifeste par une déformation mécanique (dilatation ou contraction) du matériau lorsqu’il est soumis à un champ électrique.
La piézoélectricité est présente dans plusieurs matériaux naturels, le plus emblématique étant le quartz. Toutefois, les coefficients piézoélectriques associés à ces matériaux naturels sont généralement faibles, limitant leur efficacité dans des applications industrielles exigeantes. Pour pallier ces limitations, la majorité des dispositifs modernes intègrent des matériaux synthétiques, en particulier des céramiques polycristallines à base d’oxydes de plomb, zirconium et titane, communément appelées PZT. Des oxydes additionnels peuvent être incorporés dans la formulation afin d’ajuster les constantes piézoélectriques et d’optimiser les performances du matériau.
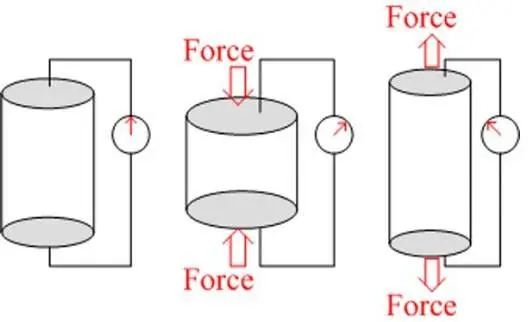
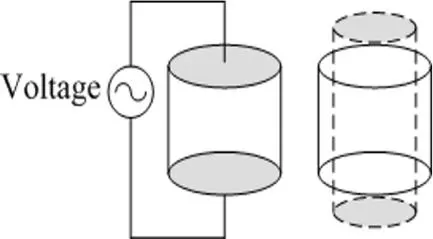
Fig. I.6. Effet piézoélectrique direct. Fig. I.7. Effet piézoélectrique indirect.
Les céramiques PZT présentent une déformabilité électrique (striction électromécanique) environ cent fois supérieure à celle du quartz, ce qui les rend particulièrement adaptées à la fabrication d’actionneurs dans de nombreuses applications industrielles. Par ailleurs, les polymères piézoélectriques tels que le PVDF (polyvinylidene fluoride) offrent des constantes piézoélectriques encore plus élevées que celles des PZT, bien qu’avec une rigidité moindre. En raison de leur flexibilité et de leur facilité d’intégration, ces polymères sont principalement utilisés dans la conception de capteurs.
________________________
2 Définition donnée par l’article 62 de la loi sur les nouvelles régulations économiques (NRE) du 15 mai 2001. ↑
3 Auchan Les 4 Temps, La Défense. ↑
Questions Fréquemment Posées
Qu’est-ce qu’une coque à double courbure en matériaux FGM?
Les coques à double courbure constituées de matériaux à gradient de propriétés (FGM) sont des structures qui présentent une distribution spatiale des propriétés matérielles, permettant d’améliorer la performance et la fiabilité dans des environnements de chargement sévères.
Comment la loi de mélange en puissance est-elle utilisée pour modéliser les coques FGM?
La loi de mélange en puissance est utilisée pour déterminer la fraction volumique locale des matériaux FGM, permettant de calculer les propriétés matérielles en fonction de la position dans l’épaisseur de la plaque.
Quelle est l’importance de la théorie raffinée de déformation par cisaillement (HSDT) dans l’analyse des coques FGM?
La théorie raffinée de déformation par cisaillement (HSDT) est essentielle pour modéliser la déformation par cisaillement transverse et les variations d’épaisseur, ce qui est crucial pour une analyse précise du comportement électro-magnéto-élastique des coques.