Analyse du cadre théorique des coques électromagnétiques : Quelles implications ?

Le cadre théorique des coques électromagnétiques révèle des comportements inattendus en flexion, remettant en question des conceptions établies. Cette recherche innovante, utilisant une théorie expo-sinusoïdale à cinq variables, promet de transformer notre compréhension des interactions entre porosité et champs électromagnétiques.

• 1. Mise en équations

Dans cette section, les équations décrivant le comportement électromécanique des matériaux piézoélectriques sont introduites selon la norme IEEE, couramment utilisée pour représenter leurs propriétés. Cette norme suppose un comportement linéaire des matériaux, une hypothèse valable lorsque les champs électriques et les contraintes mécaniques appliqués restent faibles.

Source:

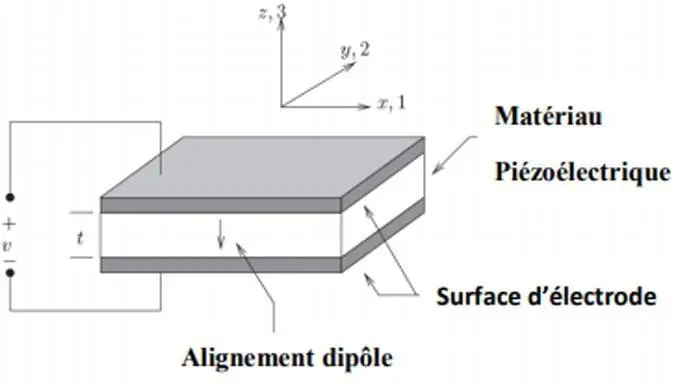
Fig. I.8. Schéma de principe d’un transducteur piézoélectrique [43].

Les équations piézoélectriques reposent sur l’hypothèse selon laquelle la déformation totale d’un transducteur résulte de la superposition de deux contributions : la déformation due à la contrainte mécanique appliquée et celle induite par l’actionnement électrique. Dans la Figure I.8, l’axe 1 correspond à la direction x, l’axe 2 à la direction y, et l’axe 3 à la direction z.

Ce dernier est défini comme l’axe de polarisation initiale de la céramique piézoélectrique, tandis que les axes 1 et 2 se trouvent dans le plan perpendiculaire. Cette convention de repérage est illustrée de manière plus explicite dans la Figure I.9. Sur cette base, les équations électromécaniques caractérisant un matériau piézoélectrique linéaire peuvent s’écrire sous la forme suivante [43, 44] :

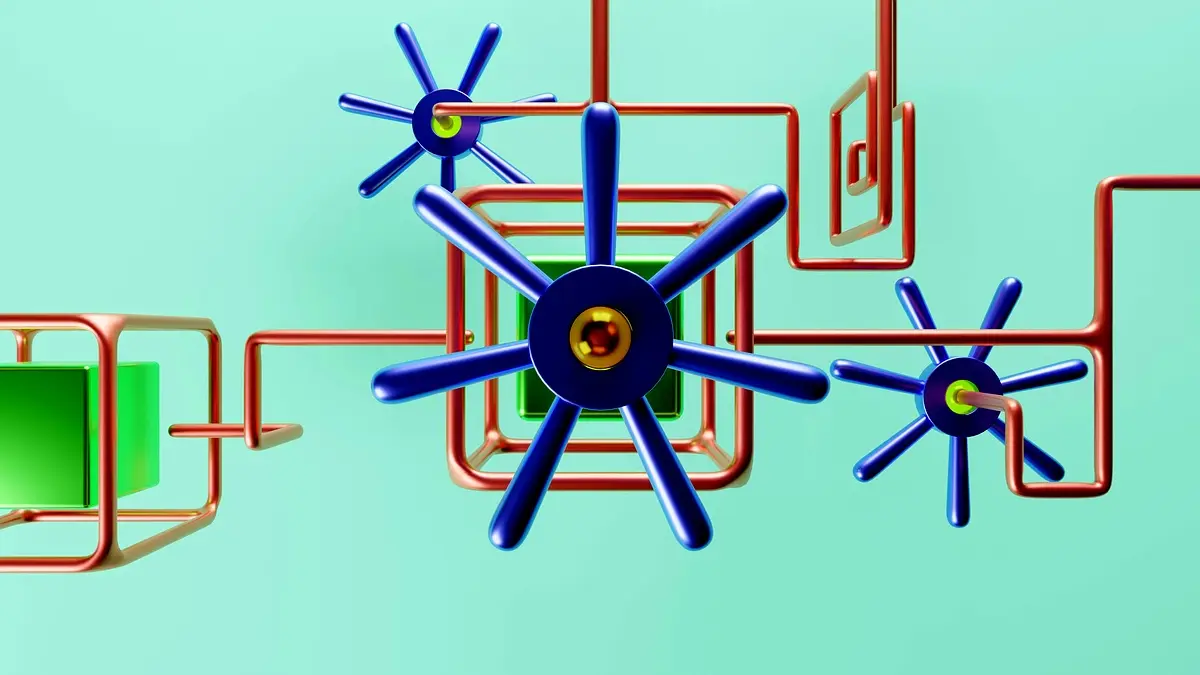
  S^E  d E

i i j j mi m

I.8

D  d   ^ E

m mi i ik k

I.9

Où les indices i, j = 1, 2, …, 6 et m, k = 1, 2, 3 font référence à différentes directions au sein du système de coordonnées du matériau, comme le montre la Figure 4. Les équations ci-dessus peuvent être réécrites sous la forme suivante, qui est souvent utilisée pour les applications impliquant la détection : [43,44]

  S^D  g D

i i j j mi m

I.10

E  g   ^ D

i mi i ik k

I.11

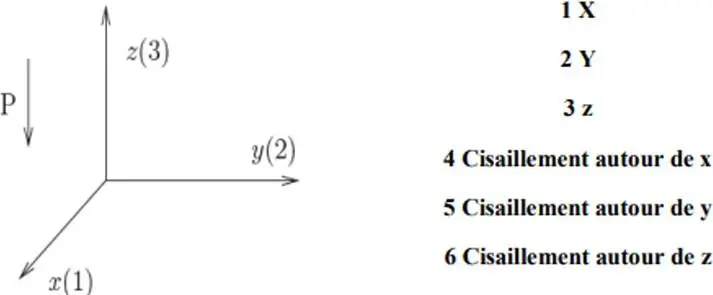
Source:

Fig. I.9. Nomenclature des axes [44].

Où :

• σ… Vecteur de contrainte (N / m²)
• ε… Vecteur de déformation (m/m)
• E… Vecteur de champ électrique appliqué (V/m)
• ξ… Permissivité (F/m)
• d… Matrice de constantes de déformation piézoélectriques (m/V)
• S… Matrice des coefficients de conformité (m²/N)
• D…Vecteur de déplacement électrique (C/m²)
• g… Matrice de constantes piézoélectriques (m²/C)
• β… Composante d’imperméabilité (m/F) D, E et σ représentent des mesures prises à déplacement électrique constant, champ électrique constant et contrainte constante.

Les équations (I.8) et (I.9) expriment l’effet piézoélectrique inverse (lorsque le dispositif est utilisé comme actionneur). Les équations (I.10) et (I.11), expriment l’effet piézoélectrique direct (qui traite le cas où le transducteur est utilisé comme un capteur). L’effet inverse est souvent utilisé pour déterminer les coefficients piézoélectriques.

L’écriture matricielle des équations (I.8) et (I.9) devient :

 1   S11 S12 S13 S14 S15 S16  1  d11 d21 d31 

  S S S S S S    d d d 

 2   21 22 23 24 25 26   2   12 23 32   E 

  S S S S S S    d d d  1

Actionnement :  3    31 32 33 34 35 36   3    13 24 33  E 

 S S S S S S 

1. d d

 2 

 4   41 42 43 44 45 46   23   14 25 34   E 

  S S S S S S    d d d   3 

 5   51 52 53 54 55 56   31   15 26 35 

6  S61 S62 S63 S64 S65 S66  12 

₁ 



d16 d27

d36 

I.12

 D  d d d d d d

 

  2  e e

e^   E 

1 11 21 31 41 51 61    11 12 13  1

Détection : D   d d d d d d   3   e^ e^ e^ E 

 2  

12 22 32 42 52 62  

 21 22 11   2 

 D  d d d d d d   4  e^ e^ e^  E 

 3  

13 23 33 43 53 63   

 ⁵ 

 31 32 33   3 

 6 

I.13

En supposant que le dispositif est polarisé le long de l’axe 3 et en considérant le matériau piézoélectrique comme un matériau isotrope transversalement, ce qui est vrai pour la céramique piézoélectrique, de nombreux paramètres dans les matrices ci-dessus seront soit nuls, soit exprimés en termes d’autres paramètres.

En particulier, les coefficients de conformité non nuls sont [44] :

S11  S22

S13  S31  S23  S32 S12  S21

S44  S55

S66  2  S11  S12 

Les constantes de déformation piézoélectrique non nulles sont :

d31  d32 et d15  d24

Enfin, les coefficients diélectriques non nuls sont 𝑒11 𝜎 =𝑒22 𝜎 et 𝑒33 𝜎. Par la suite, les équations (I.12) et (I.13) sont simplifiées pour devenir :

 ₁  S₁₁

S12

S13

0 0 0

 1   0 0

d31 

  S S S

0 0 0

 

  0 0 d 

 2  

21 22 23

  2  

³¹   E 

  S S S

0 0 0

  

 0 0

d  ¹

Actionnement : 

³   

31 32 33

  ³   

33  E 

 0 0 0

S 0 0 

0 d 0

 2 

 4  

44  

23  

¹⁵   E 

   0

0 0 0 S

0    d

0 0   3 

 ⁵  

44   31 

 15 

6   0 0 0 0 0 2(S11  S12 ) 12 

₁ 

 0 0 0 

I.14

 D   0 0 0 0 d



0 



2  e

0 0   E 

1 15

   11  1

Détection : D    0 0 0 d

0 0 

³   0 e^

0 E 

 2  

15    11   2 

 D  d d d

0 0 0  4   0 0

e^   E 

 3   13 31 33

   

 ⁵ 

33   3 

 6 

I.15

La constante de déformation piézoélectrique d est définie comme le rapport de la déformation libre développée au champ électrique appliqué. L’indice 𝑑𝑖𝑗 implique que le champ électrique est appliqué ou que la charge est collectée dans la direction i pour un déplacement ou une force dans la direction j.

Questions Fréquemment Posées

Quelles sont les équations qui décrivent le comportement électromécanique des matériaux piézoélectriques?

Les équations piézoélectriques reposent sur l’hypothèse selon laquelle la déformation totale d’un transducteur résulte de la superposition de deux contributions : la déformation due à la contrainte mécanique appliquée et celle induite par l’actionnement électrique.

Comment la théorie raffinée de déformation par cisaillement (HSDT) est-elle utilisée dans l’analyse des coques électromagnétiques?

L’étude utilise une théorie expo-sinusoïdale à cinq variables pour modéliser la déformation par cisaillement transverse et les variations d’épaisseur.

Quel est l’impact de la porosité sur la réponse des coques électromagnétiques?

Une analyse paramétrique explore l’influence du paramètre de porosité et des potentiels électrique et magnétique sur la réponse des coques.