Le cadre théorique de la commande vectorielle révèle une approche innovante pour surmonter le couplage complexe entre flux et couple dans les machines asynchrones. Cette étude met en lumière des stratégies de modulation qui transforment la performance des systèmes électriques, avec des implications significatives pour l’industrie.
Commande vectorielle de la MASDE
I.A. Introduction
La commande des machines à courant alternatif est difficile du fait qu’il existe un couplage complexe entre le flux et le couple. Cette difficulté a encouragé le développement de plusieurs techniques de commande afin que ces machines se comportent comme des machines à courant continu, caractérisées par un découplage naturel du flux et du couple. Parmi ces techniques de commande, la commande vectorielle [ARR 05].
Principe du contrôle vectoriel
Cette méthode est basée sur le choix d’un repère de référence, lié au flux rotorique. Si on décompose le courant statorique en ses composantes isq en quadrature avec ce flux, mettant en évidence une commande découplée du flux et du couple. Nous aboutissons alors des fonctionnements comparables à ceux d’une machine à courant continu à excitation séparée où le courant inducteur contrôle le flux et le courant induit contrôle le couple [RAF 05].
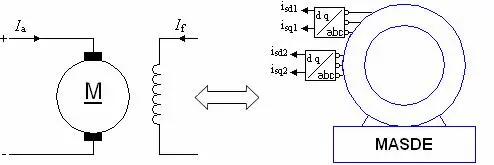
Source: URL
Modèle de la MCC

Cem=K . Ia . If
Modèle de la MASDE
Cem=K .( isd1 + isd2). (isq1 + isq2)
Fig. I.2. Principe de la commande vectorielle
Procédé d’orientation du flux
La commande vectorielle par orientation du flux rotorique permet un découplage entre le couple électromagnétique et le flux et nécessite un référentiel par une orientation du flux rotorique selon l’axe « d »:
rd r
rq 0
[I.37]
En appliquant cette condition aux équations du modèle de la machine asynchrone double étoile, nous aboutissons au système réduit suivant :
di 1
M‘ 1
M2 M‘
M M‘2 M‘
s1d
L
(R c
)i ( c R
c )i
L i c
- c v
c v
dt Lcp r
sm
s1d
Lcr r
sm s2d
cs
s cp s1q
Lcrr
Lcs
r s1d
Lcs
s2d
di 1
M‘ 1
M2 M‘
M M‘2 M‘
s2d
( R c
)i ( c R
c )i
L i c
1 c v
c v
dt
dis1q
Lcp
1
sm
r
M‘ 1
s2d
Lcr r
M2
sm s1d
cs
M‘
L
L
s cp s2q
Lcrr
M
L
r
Lcs M‘
- s2d
Lcs M‘
s1d
(R c
sm
)i ( c R
c )i
L i c
c 1 v
c v
dt Lcp r
s1q
Lcr r
sm s2q
cs
- cp s1d
cr Lcs
r s1q
Lcs
s2q
dis2q
- ( R c )i
M2
( c R
M‘
c )i L i
L
Mc
L
r
M‘
c 1
M‘
v c v
dt Lcp r
M
1
‘
sm
s2q
Lcr r
sm s1q
cs
s cp s2d
cr Lcs
r s2q
Lcs
s1q
Commande en boucle ouverte de la MASDE
Pour la commande vectorielle en boucle ouverte, nous ne procédons à aucune régulation, les différentes grandeurs de référence sont fournies à partir de fonctions de transfert déduites du modèle réduit de la machine asynchrone double étoile.
Le flux de référence est donné par un bloc de défluxage. Ce bloc de défluxage est nécessaire car il sert à diminuer le flux et donc le couple lors du fonctionnement au-delà de la vitesse nominale.
Les équations qui traduisent le bloc de défluxage s’écrivent comme suit :
avec :
r réf
rn
r
si r rn
si r rn
rn rn
[I.43]
rn : La valeur nominale du flux rotorique.
rn : La valeur nominale de la vitesse rotorique.
Dans le cas de la commande vectorielle à flux nominal, le flux de référence est maintenu constant tant que la vitesse est inférieure ou égale à la vitesse nominale, dans le cas contraire le flux doit être affaibli afin de limiter les surtensions aux bornes de la machine.
Le couple doit être borné de façon symétrique, pour ne pas dépasser le couple maximal admissible par la machine [KAR 05].
La regulation
Les régulateurs utilisés dans notre étude sont des correcteurs à action proportionnelle intégrale PI. Ce type de régulateur constitue un standard industriel, dont sa fonction de transfert est donnée par :
F ( p)
K 1 Tp
Tp
[I.44]
Calcul des paramètres de régulateur PI
Notre objectif consiste à déterminer les actions exercées sur les grandeurs de réglage vs1d, vs2d, vs1q et vs2q. Ces actions ne sont autres que les sorties de référence vs1dref, vs2dref, vs1qref et vs2qref des correcteurs représentant respectivement les valeurs instantanées souhaitées pour les tensions de réglage après découplage.
Des équations [I.42], les composantes directes et en quadrature des courants statoriques s’écrivent :
Nous posons :
Lcp
Lcs
‘
c
M
Lcs
is1d
vs1d Lcp
S
vs1q L
eq1
;
Rs
Lcp
ed1
is 2d
vs 2d
Lcp S
vs 2q
L
eq 2
Rs
Lcp
ed 2
[I.45]
is1q
cp
S Rs Lcp
; is 2q
cp
S Rs Lcp
Où ed1, ed2, eq1 et eq2 sont des termes de découplage entre les axes d et q, définis par :
eq1
M ‘
R c i
1
Lcp
s
Lcs
M ‘
1
Lcp
s
s 2 d
s Lcp
is1q
S M c
Lcr
M
( M c 1)
Lcr
1
r
M
1
M ‘
c v
Lcs
M ‘
r
s 2 d
eq 2
R c i Lcs
M ‘
1
Lcp
s
s1d
s Lcp
is 2 q
S c
Lcr
- M ‘
( c 1)
Lcr
c v Lcs
M ‘
s1d
[I.46]
ed 1
R c i Lcs
M ‘
1
Lcp
s
s 2 q
s Lcp
is1d
c
Lcr
r
M
c 1
Lcs
r
M ‘
c v Lcs
M ‘
s 2 q
ed 2
R c i Lcs
s1q s
Lcp
is 2 d r
c
Lcr
c 1
Lcs
r
c v Lcs
s1q
La machine étant découplée selon deux axes d et q, la régulation sur chacun des deux axes est faite par deux boucles interne et externe.
Les courants sur l’axe d contrôlent le flux rotorique, et ceux sur l’axe q contrôlent le couple.
Régulation sur l’axe d
I.D.1.2.2. Régulateurs des courants is1d et is2d
Pour la régulation des courants is1d et is2d, la boucle de régulation correspondante est la même pour les deux courants, et est schématisée pour le courant isd1 par la figure I.4.
_
is1d
+
s1dref
vs1d
_
eq1
i
Kid
s
pd
K
Lcp
s
1
Lcp
Rs
1
Lcp
Fig. I.4. Schéma bloc de régulation du courant is1d avec régulateur PI.
La fonction de transfert en boucle ouverte est alors :
Fids
S
K pd
Kid K pd S
1
Lcp
S Rs Lcp
[I.47]
En utilisant la méthode de compensation des pôles :
Kid
K pd
Rsm Lcp
, la fonction de transfert en boucle fermée sera :
Fids( f )
Fids
1 Fids 1
1
S Lcp K pd
[I.48]
Le temps de réponse en boucle fermée du système est :
Lcp K pd
[I.49]
Afin d’améliorer la dynamique du système, un temps de réponse pour le mode électrique t = 2 ms et choisi [MAD 97], d’où :
K pd
Lcp
et Kid
K pd
Rs Lcp
[I.50]
Régulation sur l’axe q
I.D.1.2.2. Régulation des courants isq1 et isq2
De même que sur l’axe d, nous avons une boucle interne des courants isq1 et isq2 et une boucle externe Or. De l’équation [I.42], nous constatons que les courants isq1 et isq2 ont la même dynamique que les courants isd1 et isd2, nous trouvons alors les mêmes paramètres que précédemment :
K pq
Lcp
et Kiq
K pq
. Rs Lcp
[I.51]
Synthèse de régulation de vitesse
Pour le réglage de la vitesse de rotation, nous admettons les hypothèses suivantes [ARE 01] :
La machine fonctionne à flux rotorique parfaitement réglé sur toute la plage de régulation.
Nous ne considèrons pas la régulation de la partie électrique du stator car sa constante de temps apparente est beaucoup plus réduite que la constante de temps mécanique.
La réponse des courants statoriques à leur valeur de référence apparaît comme quasi instantanée vis à vis de la partie mécanique du système.
Pour calculer les paramètres de régulation, nous choisissons les équations rotoriques du modèle avec l’équation de couple :
rd Mc (isd1
d
rd
dt
d
rq
dt
r
r
J C
M (i
isd 2 )
i )
r gl rq
d r
dt
rq c
fr r Cem
sd1 sd 2
Cr
r gl rd
[I.52]
em P
Mc
Lcr
(rd
(isq1
isq 2 )
rq (i
sd1
isd 2 ))
Nous maintenons isd1,isd 2 constants, et isq1,isq 2 signal de type échelon
(isd1
isd 2
)ref
c
rref
M
(isq1
isq 2 )ref U
[I.53]
Rr
gl
rref
Mc
Lcr
(isq1
isq 2 )
Mc U
r rref
Après arrangement des formules [I.52] et [I.53], nous obtenons:
rd rref
d
rd
dt
r
r
J C
Mc rref
U rq
rq Mc U
d
rq
dt
Mc rref
U rd
[I.54]
dt fr r
d
r
Cem Cr
P Mc
em
Lcr
(rd
U rref
Lm
rq )
Comme
(isq1
isq 2 )ref est un échelon, sa dérivée est égale à zéro en régime permanent,
ainsi nous obtenons:
2
r
r
J C
d
2 rd
dt 2
2 d rd r dt
(1 ( Tr
gl ) ) rd
2
(1 ( Tr
gl ) )
2
rref
2
dt 2
dt
2 r
fr r
d 2
rq
d
r
dt
Cem
(1 ( Tr
Cr
d
rq
2
gl rq
) )
0
[I.55]
P M c
em
Lcr
(rd
U rref
Lm
rq )
Comme nous avons :
Cemref
P Mc
Lcr
rref
( isq1 isq 2 )
[I.56]
Nous obtenons :
C (1 (Tr gl C
r
) )
2
) )
2
[I.57]
Et aussi :
em ((1
S T )2
( Tr gl
emref
r (S )
P Mc
Lcr
1
fr JS
((1 S 2
(1 (
r gl rref
)2 )
)
(
0
j
r
[I.61]
Tel que :
M (isq1 isq 2 )
r
ref
1
2
r
0
(
2
gl
1 )
2
r
[I.62]
Nous avons donc :
K 2J
et K
- (isq1
isq 2 )ref
[I.63]
p i
J
2
r
r
(isd1
isd 2
)ref
Finalement : 2J
K
p
r
et Ki
28J
2
r
[I.64]
Questions Fréquemment Posées
Qu’est-ce que la commande vectorielle pour les machines asynchrones à double étoile (MASDE)?
La commande vectorielle est une méthode qui permet un découplage entre le flux et le couple d’une machine asynchrone, en décomposant le courant statorique en ses composantes isq en quadrature avec le flux rotorique.
Comment fonctionne la commande vectorielle en boucle ouverte pour la MASDE?
Dans la commande vectorielle en boucle ouverte, aucune régulation n’est effectuée, et les grandeurs de référence sont fournies par des fonctions de transfert déduites du modèle réduit de la machine asynchrone double étoile.
Quels types de régulateurs sont utilisés dans l’étude de la commande vectorielle?
Les régulateurs utilisés sont des correcteurs à action proportionnelle intégrale (PI), qui sont un standard industriel pour la régulation des systèmes.