Analyse des propriétés élastiques des roches : résultats clés

Les propriétés élastiques des roches jouent un rôle crucial dans l’évaluation géotechnique. Cette étude révèle des méthodes sismiques innovantes, offrant des résultats surprenants sur les modules élastiques, essentiels pour comprendre la déformation du sol et optimiser les projets d’ingénierie.

CHAPITRE II : PROPRIETES PHYSIQUES DES ROCHES

Les méthodes sismiques sont des techniques d’exploration du sous-sol, basées sur l’étude de la propagation des ondes sismiques. Le comportement de ces dernières dépend des propriétés élastiques du milieu où elles se propagent. Ainsi, il est primordial de se rappeler de certains paramètres ou modules élastiques pour un corps soumis à une contrainte, sans subir une déformation permanente.

Propriétés élastiques des roches

Une contrainte  (Pression F/S) se définit comme une force par unité de surface. Lorsque la force F s’exerce perpendiculairement à la surface S, alors, il s’agit d’une contrainte de compression ou de tension suivant la direction de la force. Cependant, lorsque la force F s’exerce parallèlement à la surface S, alors, il s’agit d’une contrainte de cisaillement. Les contraintes de compression ou de tension font varier le volume mais pas la forme d’un matériau alors que les contraintes de cisaillement modifient la forme et pas le volume (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

En général, sous l’action d’une contrainte, un matériau se déforme. En effet, tout matériau soumis à des contraintes subit deux types de comportement :

• Un comportement élastique dit domaine d’élasticité. Les contraintes qui agissent sur les matériaux sont assez faibles pour qu’elles ne puissent pas engendrer des déformations permanentes ;
• Un comportement plastique dit domaine de plasticité. Ce domaine correspond à un chargement critique à partir duquel le comportement du matériau n’est plus réversible. Dans ce cas, il peut y avoir, une rupture brutale (exemple du verre), une rupture progressive (exemple du béton) ou la plastification du matériau (la forme change de façon irréversible).

A l’intérieur des limites d’élasticité, la contrainte est proportionnelle à la déformation (loi de Hooke). Cette relation de proportionnalité peut être établie par les modules d’élasticité et de cisaillement (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

Module d’allongement

Considérons un matériau parallélépipédique de longueur l et de section droite. Celui-ci est soumis à des tractions à chacune de ses deux extrémités. Si les forces ne sont pas trop fortes, on observe un allongement ε, qui est proportionnel à la longueur et aux forces. Le coefficient de proportionnalité correspond au module d’allongement. Ce module d’allongement ou module d’élasticité (longitudinale) de Young E ou encore module de traction se définit comme le rapport de la contrainte sur la déformation pour un matériau élastique isotrope dans une simple compression ou dilatation linéaire (figure 4). (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

 𝐹/𝑆 𝐹/𝑆

𝐸 = = =

[II. 1]

𝜀 ∆𝑙/𝑙 (𝑙 − 𝑙_𝑜)/𝑙

E : est le module d’élasticité de Young ;

F/S = : La force ou la contrainte appliquée par unité de surface ;

∆l/l =ε : L’allongement relatif au matériau (ou le raccourcissement) par unité de longueur sous l’effet de la contrainte.

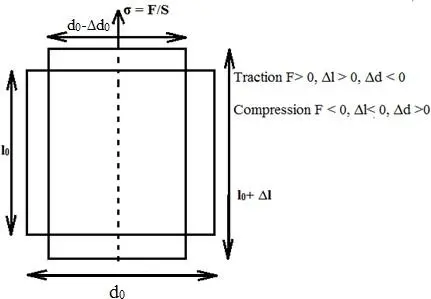
Figure 4: Relation de la contraction latérale la dilatation longitudinale

Le module de Young caractérise la résistance du matériau à la déformation uniaxiale. Il est lié aux propriétés du milieu. Dans un réseau cristallin, le comportement élastique des matériaux correspond à de petits déplacements réversibles des atomes tout autour de leur état d’équilibre (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

Coefficient de Poisson

La force F, qui a provoqué l’allongement ∆l (Figure 4), est suivie d’une contraction relative ∆d/d des arêtes perpendiculaires à la direction de la force. Le rapport de la contraction latérale à la dilatation longitudinale est appelé coefficient de Poisson.

 = ∆𝑑/𝑑 = (𝑑 − 𝑑₀)/𝑑 [II. 2]

∆𝑙/𝑙 (𝑙 − 𝑙₀)/𝑙

Le coefficient de Poisson  est un nombre sans dimension compris dans l’intervalle [0 ; 0,5]. A l’exception des élastomères, comme le caoutchouc dont le coefficient de Poisson est 

=0,5 ; la plupart des matériaux isotropes continus ont un coefficient de Poisson compris dans l’intervalle [0,25 ; 0,35] (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

Module de Coulomb

Le matériau parallélépipédique précédent subit cette fois une contrainte de cisaillement. Celle-ci provoque, sur les faces latérales, une déformation dite de cisaillement, d’un angle Ɣ (figure 5). Le rapport contrainte/déformation de cisaillement est appelé module de Coulomb.

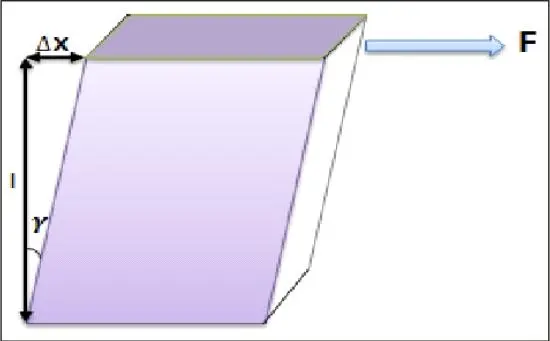
Figure 5 : Déformation de cisaillement

Le module de Coulomb μ (ou Ԍ) est également appelé module de rigidité, module de glissement ou module de cisaillement.

𝜇 = 𝐹/𝑆 [II. 3]

∆𝑥/𝑙

F/S =: La force ou la contrainte appliquée par unité de surface ;

∆x/l=tan Ɣ : Déformation de cisaillement. (Pour les petites déformations tan Ɣ≈ Ɣ) L’équation [II.3] devient :

𝜇 =  [II. 4] Ɣ

Le module de Coulomb μ rend compte de la résistance du matériau à changer de forme. Pour les liquides parfaits μ=0 ; E=0 et =0,5. Une contrainte de cisaillement change la forme d’un corps matériel et non son volume (Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base).

Module d’incompressibilité

Le module d’incompressibilité (K) représente la résistance des corps élastiques au changement de volume. Lorsqu’un matériau de volume V est soumis à une pression uniforme P dans toutes les directions, la variation de volume ∆V/V est proportionnelle à la pression P.

Le module d’incompressibilité est appelé également module global d’élasticité. Plus K est grand, plus il est difficile de réduire le volume du matériau sous l’effet de la pression P. l’inverse de K est appelé module de compressibilité β. (β = 1/K).

∆𝑉 1 𝑃

= 𝑃 𝑜𝑢 𝐾 =

[II. 5]

𝑉 𝐾 ∆𝑉/𝑉

Quelques valeurs de matériaux géologiques sont consignées dans le tableau 1 suivant :

Tableau 1 : Paramètres élastiques pour différents matériaux présents dans la subsurface (Schön 2011)

(Djeddi Mabrouk. Sismique Réflexion et Réfraction : Les Principes de Base.)

Densités des matériaux géologiques

Définition et unités

La densité est un paramètre physique qui varie en fonction de la nature des milieux géologiques. Par définition, la densité d’un corps homogène est le rapport entre sa masse et son volume.

𝑑 = 𝑚

𝑉

[𝐼𝐼. 6]

Notons que la distinction entre densité et masse volumique n’existe pas en anglais où « density » est toujours donné avec une unité et correspond à la masse volumique. La densité est donc une quantité sans dimension contrairement à la masse volumique qui s’exprime en kg • m^-3 (10^-3 g.cm^-3).

La densité d’une roche constituée de n éléments est :

𝑛

𝑑 =

𝑉_𝑖 𝑑

[𝐼𝐼. 7]

∑ (𝑉) _𝑖

𝑖=1

di : densité de l’élément i ;

Vi/V: fraction volumique de l’élément i.

Densité des constituants des roches

Les roches sont généralement hétérogènes et composées de corps appartenant aux trois états principaux qui sont : les corps gazeux, les solides et les liquides. Rappelons qu’une roche est composée d’un ensemble de minéraux variés, où la silice, le calcium et l’alumine jouent le plus grand rôle. Ces agrégats de minéraux peuvent laisser entre eux des vides remplis ou non d’eau, ou parfois d’hydrocarbures, rarement de l’air quand il s’agit de roches proches de la surface.

La densité composite d’une telle roche s’exprime par : l’expression suivante :

𝑑 = m₁ + m₂ + m₃ = M

[𝐼𝐼. 8]

v₁ + v₂ + v₃ V

Ou m1, m2, m3 et v1, v2, v3 sont respectivement les masses et les volumes de la phase solide, la phase liquide et la phase gazeuse.

Densité des minéraux

Les densités de la plupart des minéraux des roches varient de 2,2 à 3,5 10³ kgm^-3. Celles des minerais sont comprises de 4,0 à 8 10 ³ kgm^-3.

Densité des fluides des pores

La densité des liquides et des gaz est contrôlée par la composition chimique la température et la pression (la densité généralement augmente avec l’augmentation de la pression et décroit avec la température).

Eau fraiche : 1 10³ kgm^-3 ; Eau salée : 1,146 10³ kg m^-3 ; Pétrole : 0,85 10³ kgm^-3.

Densité des roches

La densité des roches dépend principalement de trois paramètres :

• Densité de grains des minéraux formant la roche ;
• Porosité  » qui représente le volume des vides par rapport au volume total de la roche » ;
• Densité du fluide remplissant les interstices de la roche.

Densité des roches magmatiques et métamorphiques

Les roches magmatiques appelées également roches éruptives ou cristallines résultent de la consolidation par cristallisation du magma en fusion. Les éléments affectants la densité des roches cristallines sont la composition, la texture, la minéralisation, la porosité et la fracturation.

Les roches métamorphiques sont les roches les plus hétérogènes du point de vue densité gravimétrique. La densité a tendance à augmenter avec le degré de métamorphisme, par suite du remplissage des espaces vides de la roche et de la cristallisation en minéraux plus denses.

Densité des roches sédimentaires

Les roches sédimentaires formées par les facteurs extérieurs sont constituées par des dépôts détritiques terrigènes, biodétritique sthalassogènes et de dépôts de précipités. Elles possèdent la densité la plus faible que les roches métamorphiques et magmatiques. Elles dépendent de plusieurs facteurs et plus particulièrement de la composition minéralogique, la porosité, l’âge géologique, l’histoire géologique, la profondeur.

Toute roche sédimentaire est constituée d’une partie solide (matrice), une partie constituée de vide (remplie généralement de fluide). La formule exprimant la densité totale de la roche s’écrit sous la forme suivante :

d = (1 − ө)dm + өdp = dm – (dm – dp)ө [𝐼𝐼. 9]

où : ө = porosité (représente le rapport du volume des vides sur le volume total de la roche. dm = densité de la matrice ;

dp = densité de la phase fluide.

Les sédiments, enfouis depuis une longue période à grande profondeur, se consolident normalement ; il en résulte une diminution de la porosité et une augmentation de la densité. Les marnes et les argiles présentent les plus fortes variations de densité en fonction de la profondeur. (Source : LA GEOPHYSIQUE POUR LES GEOLOGUES Tome 2).

Le tableau (2) suivant donne quelques valeurs de densité pour des matériaux terrestres.

Tableau 2 : Différentes densités des matériaux terrestres

(Source : « Géophysique-4^eme édition Cours et Exercices Corrigés » Page 8)

Questions Fréquemment Posées

Quelles sont les propriétés élastiques des roches?

Les propriétés élastiques des roches sont définies par des paramètres tels que le module de Young et le coefficient de Poisson, qui décrivent le comportement des matériaux sous contrainte.

Comment la méthode sismique détermine-t-elle les modules géotechniques?

La méthode sismique détermine les modules géotechniques en mesurant les vitesses de propagation des ondes sismiques à travers les différentes couches du sous-sol.

Pourquoi est-il important de connaître le module de Young?

Le module de Young caractérise la résistance du matériau à la déformation uniaxiale et est lié aux propriétés du milieu, ce qui est essentiel pour l’évaluation des propriétés du sol.