Réalisation d’un PID sous STEP7 avec le bloc de régulation
I.9- Choix et paramétrage du régulateur
Pour l’obtention d’un résultat de régulation satisfaisant, le choix du type de régulateur est déterminant.
Le paramétrage de celui-ci n’en est pas moins important, il faut donc judicieusement choisir les constantes Kp, Ti (Tn) et Td(Tv). Un compromis va généralement devoir être fait entre un système stable mais lent, et une régulation rapide avec des risques d’oscillation et donc d’instabilité.
Dans le cas d’un système non linéaire où il peut être défini un point de fonctionnement, les paramètres du régulateur devront être adaptés au comportement du système autour de ce point. S’il n’est pas possible de définir un point de fonctionnement, il faut trouver une régulation qui soit suffisamment rapide et stable pour convenir à toute la plage de travail.
En pratique, les régulateurs sont généralement paramétrés avec des valeurs obtenues de façon expérimentale. Si ces paramètres ne sont pas satisfaisants, il faudra alors pratiquer une analyse précise du système en utilisant différentes techniques ou théories pour déterminer les réglages adéquats.
Une méthode d’analyse est par exemple celle de Ziegler-Nichols par recherche de la juste oscillation. C’est une méthode simple qui s’applique à la plupart des systèmes. Cette méthode ne s’applique qu’aux systèmes dont la sortie de régulation peut être amenée à osciller. Il faut suivre le protocole suivant :
Choisir les constantes Kp et Tv du régulateur aussi petite que possible, et une grande valeur pour Tn (influence minime du régulateur) Amener manuellement le système autour de son point de fonctionnement.
Positionner manuellement la valeur régulée au niveau prédéfini avant de passer en fonctionnement automatique.
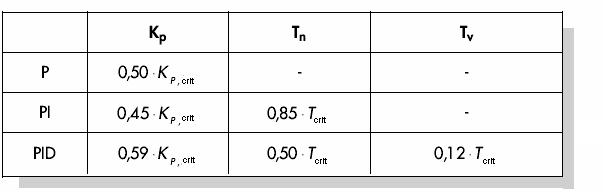
Fig.I.14 Choix et paramétrage du régulateur 22
I.10-Synthèse des systèmes asservis
La synthèse consiste à choisir la structure du correcteur et à régler ses paramètres. Ce réglage est effectué de manière à respecter des spécifications imposées par un cahier des charges. Ainsi, il peut être demandé d’avoir :
- Une bonne précision statique (régime permanent).
- Un faible temps de réponse (précision dynamique).
- Un bon rejet des perturbations, problème de régulation.
- Un bon suivi de trajectoire, problème de poursuite.
- Une bonne stabilité.
- Une bonne robustesse (garantir le bon fonctionnement sur le procédé réel)
- Etc.
I.10.1-Performances d’un système asservi
Le régime transitoire de la réponse temporelle y(t) d’un système excité par une consigne en échelon peut être caractérisé par un ou plusieurs indicateurs de rapidité et d’amortissement qui sont :
- Le temps de montée (noté tm) qui correspond au temps nécessaire pour que la sortie y(t) passe de 10% à 90% de sa valeur finale.
- Le temps de réponse à 5% (noté tr), temps à partir duquel la sortie y(t) reste inférieure à 5% de sa valeur finale.
- Le dépassement (noté D%) (s’il y en a un) : c’est la valeur maximale de y(t) divisée par la valeur finale exprimée en %. C’est le 1er maximum.
- Le temps du 1er maximum (s’il y en a un) tmax est le temps pour lequel se produit le premier dépassement.
Fig.I.15 Performances d’un système asservi
I.10.2-Réponse indicielle
On observe la commande d’un régulateur en réponse à un échelon d’erreur. La réponse est alors composée de trois parties distinctes :
- Un pic résultant de l’action dérivée.
- Un échelon résultant de l’action proportionnelle.
- Une rampe résultant de l’action intégrale.
Fig.I.16 Réponse indicielle
I.11- Réalisation d’un PID sous STEP7 avec le bloc de régulation continue (S) FB41″CONT_C »
I.11.1- Régulateur PID
Le bloc FB 41 « CONT_C » sert à régler des processus industriels à grandeurs d’entrée et de sortie continues sur les automates programmables SIMATIC S7. Le paramétrage permet d’activer ou de désactiver des fonctions partielles du régulateur PID et donc d’adapter ce dernier au système réglé.
Nous pouvons utiliser le régulateur comme régulateur PID de maintien autonome mais aussi comme régulateur en cascade, de mélange ou de rapport dans des régulations à plusieurs boucles.
Sa méthode de travail se base sur l’algorithme PID du régulateur à échantillonnage à sortie analogique, complété le cas échéant par un étage conformateur d’impulsions assurant la formation des signaux de sortie à Modulation de largeur d’impulsions pour régulations à deux ou trois échelons avec Organes de réglage proportionnels.
I.11.1.1-Tableau récapitulatif des entrées / sorties utilisées dans l’exemple
Fig.I.17 Tableau récapitulatif des entrées / sorties
I.11.2-Description
En plus des fonctions traitant la consigne et la mesure, le FB réalise un régulateur PID prêt à l’emploi avec sortie continue de la grandeur de réglage et possibilité d’influencer à la main la valeur de réglage.
Selon le type de CPU, il sera mis en œuvre grâce au FB41 (pour les CPU 3xx-2DP) ou au SFB41 (pour les CPU sans interface Profibus).
Il propose les fonctions partielles suivantes :
- Branche de consigne
- Branche de mesure
- Formation du signal d’erreur
- Algorithme PID
- Traitement de la valeur de réglage manuelle
- Traitement de la valeur de réglage
- Action anticipatrice
I.11.3- Etats de fonctionnement
Le bloc FB 41 « CONT_C » dispose d’un sous-programme de démarrage qui est exécuté quand le paramètre d’entrée COM_RST = TRUE. A la mise en route, l’intégrateur est positionné de façon interne sur la valeur d’initialisation I_ITVAL. En cas d’appel dans un niveau d’alarme d’horloge, il continue à travailler à partir de cette valeur. Toutes les autres sorties sont positionnées sur leurs valeurs par défaut.
I.11.4-Informations d’erreur
Le bloc ne procède pas à un contrôle interne d’erreur. Le mot indicateur d’erreur RET_VAL n’est pas employé.
I.12-Identification du procédé
L’identification a pour objectif de rechercher la fonction de transfert du procédé à réguler, c’est-à-dire un modèle mathématique représentant le plus fidèlement possible le comportement du ce procédé autour de son régime nominale.
La recherche des paramètres de la fonction de transfert du modèle S’effectue à partir de l’enregistrement du signal d’entrée u (échelon manuel) et du signal de sortie y (mesure de la réponse de la grandeur réglée).
La fonction de transfert réelle d’un processus industriel est pratiquement impossible à déterminer, car les processus industriels sont en général non linéaires sur toute leur plage de fonctionnement.
C’est pourquoi on se limite à de faibles variations autour d’un point de fonctionnement ou régime nominale (et on considère que le processus est linéaire de type fonction de transfert).
I.12.1 Identification en boucle fermée
I.12.1.1Méthodologie
La procédure est simple. On applique une variation d’entrée U (impulsion, échelon ou rampe) et on observe l’évolution de la variation de la mesure Y(t) (la grandeur réglée).
La méthode nécessite la mise en oscillations entretenues de la boucle de régulation.
Fig.I.18 Schéma fonctionnelle d’un système en boucle fermée
Fig.I.19 Signaux d’entrées U(t) utilisés
I.12.1Méthode de Broïda
Broïda s’intéresse aux processus stables, et procède à une identification en boucle ouverte. Mais il simplifie en considérant que la forme de la réponse peut être assimilée à une fonction mathématique du premier ordre avec une constante de temps T, assortie d’un retard pur τ :
Fig.I.20 Réponse Y(t) (de modèle de Broïda) suite à un échelon d’entrée
I.13-Avantages et inconvénients du correcteurs P, PI, PD et PID
Fig.I.21 Avantages et inconvénients du PID
I.14-Conclusion
Dans ce chapitre, nous avons présenté les différentes méthodes de régulation en boucle ouverte et en boucle fermée, une description générale des systèmes industriels ainsi que quelques méthodes de régulation, qui se résument dans l’utilisation des régulateurs PID.
Dans le chapitre suivant nous présentons la logique et commande floue.