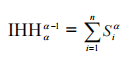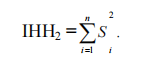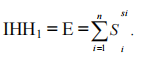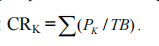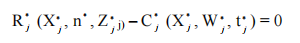Mesure de la concurrence bancaire : structurelle et non structurelle
Section 2 :
Mesure de la concurrence bancaire
Il existe différentes méthodes de mesure de la concurrence, on peut distinguer deux principales classes :
- approches structurelles et
- approche non structurelles.
Les approches structurelles décrivent la structure de marché avec le rôle central des ratios de concentration dans l’industrie.
Les exemples de ce type d’approches sont :
- L’approche « structure-comportement-performance » (SCP).
- La théorie de la structure efficiente.
- Un nombre d’approches formelles qui ont des racines dans la théorie de l’organisation industrielle.
2. 1 Mesure structurelle de la concurrence
Les approches structurelles peuvent être divisées en deux approches : les approches formelles et les approches non formelles.
2. 1. 1 Les approches formelles
On distingue deux approches formelles qui étudient la relation entre la concurrence et la concentration : l’indice Herfindahl-Hirshman et le ratio de concentration bancaire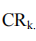
2. 1. 1. 1 L’indice Herfindahl-Hirshman (IHH)
L’indice de Herfindahl-Hirshman est extrait du nom de deux économistes américains, et utilise principalement le terme part de marché. Il est définit comme étant la somme des carrées de la part de chaque entreprise dans un marché particulier.
C’est un indice cumulatif dans lequel chaque entreprise est pondérée par sa part de marché : 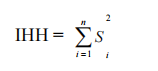
Où Si: la part du marché de la banque de rang i.
On peut déduire :
- Si IHH = 1 : c’est la valeur maximale ⇨ situation monopole.
- Si IHH = 1/n: c’est la valeur minimale ⇨ situation de concurrence.
Si on a n entreprises possédant des tailles égales. Alors chaque entreprise a comme part de marché :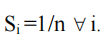
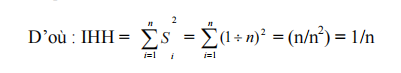
On obtient l’interprétation suivante
- Si IHH tend vers 1 : on peut parler d’une branche assez concentrée.
- Si IHH tend vers 1/n : on dit qu’on a une situation concurrentielle.
L’indice IHH permet d’obtenir un premier éclairage sur l’augmentation
(ou la diminution) du degré de concentration d’une branche économique dans un marché bien délimité.
Les économistes peuvent ensuite analyser et évaluer les conséquences afférentes au changement du degré de concentration.
On note que cet indice, dans la théorie économique, permet d’étudier essentiellement la marge du prix sur le coût.
Soit IHHα est l’indice élargie de Herfindahl, c’est l’indice le plus connue et le plus utilisé pour mesurer la concentration au sein du marché.
On note, selon que l’on prend pourα, on obtient un indice de concentration particulier, c’est-à-dire :
- Si on prend α = 2, on revient aux analyses de l’indice précédent,
- Si on prend α = 3, on a un indice Herfindahl de rang supérieur qui accentue encore le poids des grandes unités, de façon que la place prise par les petites unités est encore plus faible qu’avec H2.
- Pour α = 1, c’est le cas limite, dont on obtient l’indice exponentiel qu’est lié à l’entropie :

L’indice de H. H possède deux avantages sur les autres ratios de concentration puisqu’il tient compte de :
- Tous les participants sur un marché donné.
- La structure industrielle, et donc du risque de coordination des comportements.
2.1.1.2 Les ratios de concentration
Cet indice tient compte, la part de marché de K premières entreprises du secteur. C’est l’indice le plus utilisé dans les études empiriques sur la concentration malgré qu’il soit beaucoup plus restreint.
Avec : 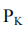 : est la part de marché de K plus grandes banques.
: est la part de marché de K plus grandes banques.
TB : est le total bilan, on peut utiliser aussi d’autres totaux comme total dépôt, total crédit, fond propre,…
Ainsi, par exemple pour mesurer la concentration dans 23 pays européennes, Bikker et Haaf (2002) ont utilisé les ratios CR3 ; CR5 et CR10.
Toutefois, pour que l’expression C soit une mesure de la concentration, elle doit réunir les trois conditions suivantes :
- Le transfert de la part de marché d’une firme à une autre doit se refléter dans la valeur de l’indice.
- La concentration ne doit pas décroître en cas de fusion des firmes du secteur.
- La mesure de la concentration doit être une fonction décroissante du nombre des firmes lorsque celles-ci sont de tailles égales.
2.1.2 Les approches non formelles
Il y a deux exemples d’approches non formelles :
- L’approche « Structure-Comportement-Performance » (SCP).
- L’approche « structure efficiente ».
2.1.2.1 L’approche SCP
Le modèle Structure-Comportement-Performance constitue le modèle de référence de la théorie de l’organisation industrielle. Il a été largement appliqué dans les années 1960 et 1970 à l’industrie bancaire.
Ce modèle permet d’expliciter les effets attendus de la présence de certaines caractéristiques du marché (la concentration de l’offre, les barrières réglementaires à l’entrée) sur l’état de la concurrence dans l’industrie bancaire.
L’idée fondamentale de ce modèle est que les comportements et les conflits dans une industrie sont déterminés par ses structures.
Autrement dit, les résultats des firmes sont déterminés d’une part par le nombre, la taille et la concentration des offreurs, et d’autre part les conditions d’entrée et la réglementation du marché.
Dans ce modèle, la plupart des industries ont des structures intermédiaires entre la concurrence parfaite et le monopole.
La question est alors de savoir dans quelle mesure le niveau des prix et celui des profits demeurent proches de ceux de la concurrence ou, au contraire s’approche de ceux du monopole. Le critère de référence est celui d’une structure productive efficiente.
Ainsi selon cette approche, si les entreprises parviennent à coordonner leurs activités, elles appliquent alors les prix de monopole.
Or dans une entente, chaque entreprise a intérêt à ne pas respecter les termes de l’accord et à abaisser ses prix de façon à accroître sa part de marché aux dépend des autres.
Dans le modèle Structure-Comportement-Performance, les résultats des entreprises sont déterminés par les structures du marché. L’ensemble de ces relations figure sur le graphique suivant:
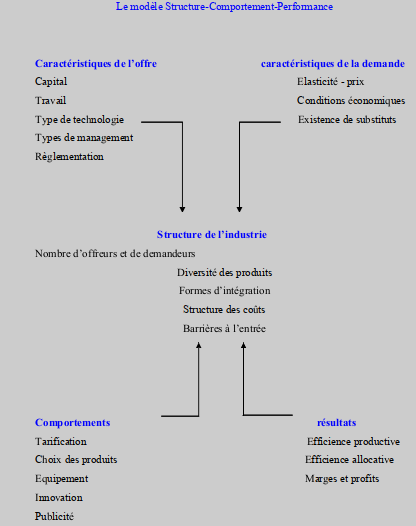
Sources : Dietesch M. (1992) : « Quel modèle de concurrence dans l’industrie bancaire ? », revue économique n°2, pp 229-295.
2.1.2.2 La théorie de la « Structure – efficiente »
La théorie « structure – efficiente » a été développée par Demstez (1973). Elle indique que les firmes efficientes augmentent en taille et en part de marché à cause de leur aptitude à générer des profits élevés, qui d’habitude menait à une concentration de marché levée.
Donc la relation positive entre les profits et la concentration est expliquée par les coûts bas achevés par la supériorité managériale ou la performance du processus de production.
Donc la théorie « structure – efficiente » justifie la concentration et la profitabilité d’un secteur par le comportement efficient de certaines de ces composantes par rapport à leurs rivales.
Les mesures non formelles de la concurrence (modèle SCP, « structure – efficiente ») fournissent des politiques de marché pour mesurer la performance et la structure de marché. On constate aussi que ces deux aspects ont été fréquemment appliqués à l’industrie bancaire (Bikker et Haaf, 2002).
2.2 Mesure non structurelle de la concurrence
Devant les manques théoriques et empiriques des modèles structurels, les modèles non structurels de mesure de la concurrence ont été développés pour donner : le modèle Iwata (1974), le modèle Bresnahan (1982) et le modèle Panzar et Rosse (1987).
Cependant, d’après Toolsema (2002) seulement les deux dernières méthodes dominent les études récentes pour mesurer la concurrence dans les marchés bancaires.
2.2.1 Le modèle Panzar et Rosse
Le modèle Panzar et Rosse (1987) présente une mesure du pouvoir de marché et des conditions concurrentielles d’un secteur, à partir de la conséquence de l’impact des prix des facteurs de production sur les revenus des entités constitutives du secteur.
Panzar et Rosse ont montré que ♣:
- En situation de concurrence pure et parfaite, partant de l’hypothèse que les entreprises produisent à leur niveau d’équilibre de long terme, la croissance du prix des facteurs de production crée une croissance proportionnelle des revenus. Le volume d’outputs minimisant les coûts moyens ne varie pas tandis que le prix de cet output évolue sa part dans la même proportion que les prix des inputs de production.
- En configuration intermédiaire de concurrence monopolistique, les revenus croissent proportionnellement moins que les prix des facteurs. La demande régnant sur le marché étant inélastique.
- A l’autre extrémité, le cas de monopole de marché décrit quant à lui une situation dans laquelle une croissance des prix des inputs met en cause les coûts marginaux, réduisant ainsi le niveau de production d’équilibre et de revenus. Dans cette configuration, la réponse des revenus est nulle voire négative.
Cette approche suppose de manière cruciale que les banques sont à leur équilibre de long terme. De plus la performance des banques est indépendante du comportement des autres banques dans l’industrie.
♣Panzar J. C and Rosse J. N (1987): « Testing for monopoly equilibrium », Journal of industrial Economics, 35, pp 443-456.
Une autre hypothèse est que le prix de l’élasticité de la demande est ramené à l’unité. Les banques maximisent leurs profits et par la suite l’industrie bancaire est considérée dans son ensemble. Ceci signifie que le revenu marginal bancaire est égal au coût marginal : 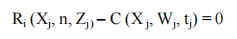
Où 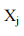 l’output de la banque j, n le nombre de banque,
l’output de la banque j, n le nombre de banque, 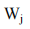 les prix des inputs de la banque j,
les prix des inputs de la banque j, 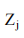 est le vecteur des variables exogènes qui modifient la fonction du revenu bancaire,
est le vecteur des variables exogènes qui modifient la fonction du revenu bancaire, 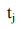 est un vecteur de variables exogènes qui modifient la fonction coût bancaire (Bikker et Haaf 2002). En équilibre la contrainte zéro profit est maintenu pour le marché entier :
est un vecteur de variables exogènes qui modifient la fonction coût bancaire (Bikker et Haaf 2002). En équilibre la contrainte zéro profit est maintenu pour le marché entier :
Les variables en (*) représentent les valeurs d’équilibre.
Le pouvoir de marché est mesuré par la portée duquel le changement des prix des facteurs de production 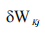 est reflété dans les revenus d’équilibre
est reflété dans les revenus d’équilibre 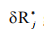 gagné par la banque j (Bikker et Haaf 2002).
gagné par la banque j (Bikker et Haaf 2002).
Panzar et Rosse ont tiré un test de concurrence fondé sur l’estimation d’une fonction de revenu dans sa forme réduite. Le calcul de la statistique H est défini comme la somme des élasticités des revenus bancaires aux variations des prix des inputs :
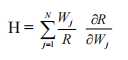
Cette statistique permet d’évaluer le degré de concurrence régnant sur les marchés bancaires. En effet :
- Si H = 1 : on accepte l’hypothèse de marché en situation de concurrence pure et parfaite.
- Si H ≤ 0 : on accepte l’hypothèse de l’existence d’un monopole de marché.
- Si 0 < H ≤ 0 : on accepte l’hypothèse de marché sous régime de concurrence monopolistique.
Le modèle Panzar et Rosse a été appliqué par plusieurs auteurs comme le montre le tableau suivant :
Tableau 1 : Les différentes applications du modèle de Panzar et Rosse
| Auteurs | Pays étudié | Période | Résultats |
| Molyneux, Williams et Tharnton (1994). | Allemagne, Espagne, France, Italie et le Royaume Uni. | 1986 – 1989 | Concurrence monopolistique pour la France, l’Allemagne, l’Espagne, le Royaume-Uni et l’Italie. |
| Vesala (1995). | Finlande. | 1985 -1992 | Concurrence Monopolistique. |
| Coccorese (1998). | Italie | 1988 – 1996 | Concurrence Monopolistique. |
| Rime (1999). | Suisse | 1987 – 1994 | Concurrence Monopolistique. |
| Bikker et Groenevid (2000). | 15 états européens. | 1989 – 1996 | Concurrence Monopolistique. |
| De Bandt et Davis (2000). | Allemagne, France et Italie. | 1992 – 1996 | ▪ « Grandes »banques : concurrence monopolistique pour tous les états. ▪ « Petites » banques : concurrence monopolistique en Italie et monopole en France et en Allemagne. |
| Maudos et Pérez (2001). | Espagne | 1992 – 1999 | Concurrence Monopolistique. |
| Bikker et Haaf (2002). | 23 pays de l’OCDE (dont 17 états européens. ) | 1991 – 1997 | Concurrence Monopolistique. |
Source : Michel Boutillier, Jimmy Gaudin, Stéphanie Grand Perrin (2004) : « la situation concurrentielle de principaux secteurs bancaires européens entre 1993 et 2000 : Quels enseignements pour la futures structure de marché financiers issue de l’UEM ? ».
De même le modèle Panzar et Rosse (1987) a été utilisé par Thierry Buchs et Johan Mathisen en janvier 2003 pour évaluer la concurrence bancaire au Ghana. Ils ont trouvé que les banques se comportent d’une manière non concurrentielle ce qui gène l’intermédiation financière. ♠
2.2.2 Le modèle Bresnahan-Lau
Un outil alternatif est la méthode de variations conjoncturelle. La base de cette méthode est développée par Iwata (1974). Cette approche nécessite aussi l’estimation d’un système des équations.
Bresnahan (1982) et Lau (1982) ont résolu le problème d’identification de l’estimation économétrique du modèle Iwata. Les deux auteurs utilisent une paramétrisation alternative bornée par l’élasticité de la variation conjoncturelle. ♣
Comme il est mentionné avant, les deux modèles Iwata et Bresnahan – Lau sont deux principales mesures non structurelles de la concurrence basées sur la théorie de l’organisation industrielle.
Cependant, d’après Bikker et Haaf (2002), le modèle Iwata avait été appliqué une seule fois à l’industrie bancaire.
L’utilisation rare de cette approche est due au manque des données nécessaires suons la structure de coût et de production d’un certain nombre d’acteurs de l’industrie bancaire dans plusieurs pays.
Contrairement au modèle Iwata, le modèle Bresnahan – Lau est beaucoup plus utilisé dans plusieurs pays pour analyser l’industrie bancaire.
♠ Buchs et Mathiens (2003): « Banking competition and efficiency in Ghana » Working papers. ♣ Bresnahan T (1982): « The oligopoly solution concept is identified, Economic Letters, n 10, pp 87-92.
Le modèle Bresnahan – Lau est un modèle statique à court terme qui détermine empiriquement le pouvoir de marché. Dans ce modèle une variation conjoncturelle des paramètres est déterminée, basée sur une série de données temporelles relatives à l’industrie.
Il est achevé par l’estimation simultanée de la demande de marché et la courbe d’offre. Du fait qu’il est un modèle statique, alors il a peu d’inconvénients.
Le modèle dépend de certaines hypothèses dont :
- Le test compte sur la maximisation des profits des firmes qui suppose l’égalité entre le coût marginal fixe et leur revenu marginal perçu, qui coïncide avec le prix de la demande dans les équilibres concurrentiels mais correspond au revenu marginal dans les cas extrêmes.
- Les banques sont considérées comme preneurs des prix en ce qui concerne leurs inputs (par exemple les fonds sont obtenus à travers le marché monétaire).
- Les banques sont supposées avoir un risque neutre.
Le modèle estime les réponses bancaires anticipées face au changement des outputs des concurrents. La fonction de revenu marginal de la banque est : P + h (Q, Y,α) ;
Où P est le prix de l’industrie, Q est la quantité de l’output totale, Y est le vecteur de variables exogènes et α est un vecteur de paramètre relatif au système de demande estimée (Bresnahan, 1982).
A cette équation un autre paramètre λ peut être ajouté. λ est le nouveau paramètre à estimer et h (. ) est la demi élasticité de la demande de marché.
La nouvelle équation est : P + λ h (Q, Y,α) ;
Où λ représente, l’étendue à la quelle les firmes reconnaissent la distinction entre les fonctions du revenu marginal.
Ainsi la variable λ peut avoir les valeurs suivantes :
- λ = 0 pour les banques de taille moyenne dans un marché parfaitement concurrentiel.
- λ = 1 pour une collusion parfaite dans le marché.
- 0 < λ < 1 degré de varié de concurrence imparfaite ou collusion.
Donc il y a plusieurs façons pour mesurer la concurrence, on trouve les approches structurelles tels que la théorie SCP, le courant « structure efficiente » et d’autres approches formelles.
Les approches non structurelles contiennent le modèle Panzar et Rosse et le modèle de Bresnahan-Lau.
Les premières approches insistent sur l’importance de la structure de marché, alors que les deuxièmes insistent sur l’analyse du comportement concurrentiel des banques sans utiliser les informations explicites sur la structure de marché.