3. Méthodes de synthèse d’opinions d’experts
Fustier (1993) s’intéresse à l’évaluation de l’espace rural, dans le sens où il cherche à mettre au point une méthode qui permettrait non seulement de dire si « oui » ou « non » une zone est rurale mais aussi, le cas échéant, à quel point elle l’est. Il s’agit donc d’abord de déterminer les critères sur lesquels on doit se baser pour estimer la « ruralité » de la zone avant (peut-être) de mesurer ces critères afin d’obtenir son degré de « ruralité ».
3.1. L’approche ensembliste traditionnelle
Ici, l’espace rural est considéré à juste titre comme étant une partie de l’espace tout entier, il est un sous-ensemble de l’espace National. Ce sous-ensemble est décomposé en classes d’équivalences correspondant au degré de « ruralité » des zones.
Les zones sont, comme nous l’avons proposé dans cette étude, représentées par un faisceau de caractéristiques, « une suite pratiquement infinie d’attributs hétérogènes, des nombres assortis d’unités de mesure différentes pour les caractéristiques quantitatives, des mots pour les caractéristiques qualitatives » (Fustier 1993). Ainsi, une zone (un lieu) peut être représentée sous la forme d’un tableau comme celui-ci :
| Caractéristiques quantitatives | Caractéristiques qualitatives | ||||||
| population | salaire moyen | altitude | .. | esthétique du paysage | patrimoine écologique | qualité des eaux | .. |
| 2343 habitants | 107 (indice) | 50 mètres | .. | agréable | moyen | acceptable | .. |
A partir de là, les zones disposant des caractéristiques que l’on estime associées à l’idée de « ruralité » seront détectables et classées comme zones rurales. Deux zones rurales devront donc avoir des faisceaux de caractéristiques similaires et quasi identiques si elles font de plus partie de la même classe d’équivalence (si elles ont le même degré de « ruralité »).
On entrevoit déjà la difficulté que peut rencontrer le chercheur chargé d’évaluer un grand nombre de zones afin d’en déduire l’appartenance ou la non-appartenance à l’espace rural, sans parler de la difficulté quasiment insurmontable de trouver des zones présentant, au niveau de leur faisceau et donc de toutes leurs caractéristiques, des similitudes telles qu’elles pourraient appartenir à une même classe d’équivalence, qui auraient en fait le même degré de « ruralité ». La tâche est pour le moins complexe.
Dans la pratique, on ne tient compte que de certaines caractéristiques, les plus en rapport, les plus influentes sur l’aspect traité. On comprend que la moyenne d’âge des habitants de la zone ne soit pas un élément pertinent quant à sa classification en zone rurale (bien qu’il puisse en être une conséquence). Autre simplification et non des moindres, on ne tient compte en réalité que des caractéristiques quantitatives. Enfin, notons que l’on utilise parfois une approche pour le moins simpliste puisqu’elle ne prend en compte qu’une caractéristique quantitative.
Dans l’exemple présenté ici, on peut supposer que la population résume toutes les autres caractéristiques de ruralité puisque statistiquement, la population est corrélée négativement avec l’ensemble de ces caractéristiques. La loi d’appartenance est alors définie comme suit :
Considérant la zone z et pop(z) sa population,
- si pop (z) 2000 habitants, alors z est rurale
- si pop (z) > 2000 habitants, alors z est non rurale
Les classes d’équivalences sont ensuite constituées de zones comptant un nombre d’habitant similaire, correspondant donc à un degré de ruralité semblable. Par exemple :
si pop(z) [0, 60[ alors z appartient à R1 = classe de forte ruralité.
si pop(z) [60, 600[ alors z appartient à R2 = classe de ruralité moyenne.
si pop(z) [600, 2000[ alors z appartient à R3 = classe de faible ruralité.
Cette approche est certes facilement applicable mais ne reposant que sur une caractéristique (même si importante), elle demeure très réductrice. Elle est surtout conventionnelle, partant d’une règle qui peut être discutée.
Une seconde approche, plus réaliste, se propose en quelque sorte de vérifier les résultats obtenus par la précédente (basée sur la population) en utilisant plusieurs autres caractéristiques de la ruralité comme la surface consacrée aux cultures agricoles (AGR), le nombre de bâtiments affectés aux services publics (PUBL), la surface non cultivée et laissée à l’abandon (ABON) etc.
Dans cette approche, c’est la prise en compte successive de ces différents critères qui subdivisera le territoire de départ en zones de différents degrés de ruralité. On commencera par retenir le critère qui semble le plus lié à la population (selon un critère statistique donné, ce pourra être le chi-deux, les moindres carrés ou autre), ce critère permettra alors de distinguer deux (ou plus) espaces sur lesquels on cherchera à nouveau (et toujours selon la même technique statistique) la caractéristique la plus liée à la population afin de l’utiliser pour une nouvelle « segmentation du sous-espace ainsi obtenu et ainsi de suite.
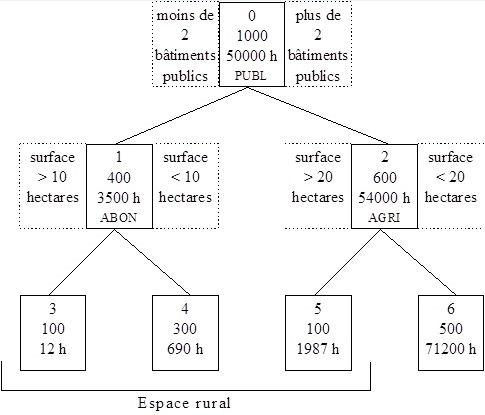
Une représentation de la procédure et des résultats pourrait être la suivante :
On indique dans chaque case :
- Le numéro du segment (0 = espace de départ, le territoire étudié)
- Son effectif (nombre de lieux)
- La valeur moyenne de la population des lieux affectés au segment considéré
- La caractéristique la plus liée à la population.
L’une des particularités de cette approche, visible sur l’exemple que l’on vient de voir, c’est qu’elle détermine l’appartenance à une classe d’équivalence avant même que l’on définisse les classes qui constitueront l’espace rural. Il est également intéressant de constater que la critique que nous faisions à la précédente méthode n’a pas lieu d’être ici, puisque les seuils d’affectation sont déterminés statistiquement et non plus de manière conventionnelle, ce qui la rend plus fiable.
Ce qui ne doit pas nous empêcher de nous interroger sur la fiabilité des données sur lesquelles elle repose. Comment sait-on qu’une caractéristique est une caractéristique de ruralité ? Même si certaines d’entre elles semblent logiquement avoir un lien étroit et reconnu par tous avec la notion de ruralité, son intervention dans la segmentation pourra quand même donner lieu à des discussions entre les chercheurs.
En effet, si la prise en compte du nombre de bâtiments publics semble intéressante ici, on peut se demander pourquoi les zones devraient appartenir à deux catégories différentes parce que l’une d’elles en compte deux alors que l’autre en regroupe trois ; le résultat final ne serait pas le même si la différence se faisait à partir de quatre établissements publics.
Soulignons également que les caractéristiques qualitatives sont souvent exclues de l’analyse et que d’autres sont estimées à l’aide d’indicateurs parfois discutables. Enfin, toutes ces remarques conduisent à la même conclusion ; par ce type de méthode, l’appartenance ou non d’une zone à l’espace rural risque d’ètre déterminée à partir d’infimes nuances, la distinction « rurale » « non-rurale » ne tenant qu’à certains paramètres évolutifs à discrétion.
La méthode suivante tente de résoudre cette imperfection en établissant une frontière moins tranchée entre le oui et le non. Elle vise à remplacer le résultat « appartient »-« n’appartient pas » par le résultat « appartient plus ou moins ».
3.2. Evaluation de notions floues par le « flou »
L’idée de départ est relativement simple, l’appartenance d’une zone à l’espace rural ne doit plus dépendre du dépassement (ou non) du seuil fixé sur un critère, mais le seuil atteint dans ce critère va déterminer le degré de ruralité de la zone. Pour simplifier, dans la première méthode, on considère que la zone z est rurale si elle possède une faible population.
Le seuil de passage entre une population faible et une population forte étant un nombre fixe, la limite entre une zone rurale et une zone non rurale est « brutale ». En effet, la population est soit faible, soit forte, on ne peut donc répondre à la question « z est-elle une zone rurale ? » que par oui ou non, selon que la proposition « z possède une faible population » est vraie ou fausse. Dans le langage Booléen, on utilise le 1 si la proposition est vérifiée, le 0 si elle ne l’est pas (il n’y a pas d’autre alternative). Ainsi, si :
- pop (z) = 1 (la population de z est effectivement faible), alors z est rurale.
- pop (z) = 0 z non rurale.
3.2.1. Principe du « flou »
Une nouvelle méthode consiste alors à établir des « échelons de véracité » de la proposition auxquels correspondront alors différents niveaux de ruralité (pour notre exemple). Pour formaliser cette idée, Zadeh (1965) remplace le couple de réponses (0;1) par l’intervalle de réponse [0;1] on voit alors apparaître une infinité de niveaux de vérité de la proposition et par la même une infinité de degrés d’appartenance à l’espace rural. Exemple :
- pop (z) = 0,9 (la population de z est faible : presque vraie) z appartient presque totalement à l’espace rural.
- pop (z) = 0,2 (proposition assez fausse) z appartient peu à l’espace rural.
La difficulté liée à l’estimation de franchissement ou non d’un seuil strict est certes résolue, mais la trop grande quantité d’échelons va poser un problème du même type puisque la différenciation risque de devenir trop sensible et donc difficilement perceptible par le chercheur. On aura du mal à faire la différence entre 0,25 et 0,26.
Et même s’il est plus aisé de qualifier ces niveaux de vérité dans le langage courant que de leur donner une valeur numérique précise, la différence entre « z est une zone plutôt rurale » et « z est une zone relativement rurale » n’en demeurera pas moins délicate. L’idéal serait en fait de disposer de niveaux de vérité en quantité suffisamment restreinte pour que chacun des échelons se distingue facilement des autres. « L’échelle de vérité » proposée par Fustier (1991) semble pour cette raison la mieux appropriée :
« Cette échelle intègre les cas extrêmes faux et vrai, car malgré l’imprécision inhérente à des caractéristiques comme faible population, on n’écarte pas la possibilité du tout ou rien pour des lieux très spécifiques. D’autre part, on observe que chaque élément ou échelon possède un opposé, c’est à dire un attribut qui, dans le langage courant, possède un sens opposé au premier » (Fustier 1991). On obtient les opposés en inversant l’échelle de vérité.
Outre l’avantage lié au fait que cette échelle de vérité permet d’évaluer plus facilement des critères « flous » (notamment des critères qualitatifs, nous l’avons vu, qu’il est quasiment impossible de quantifier, chose qui serait de toute manière contre nature), cette méthode d’évaluation présente également l’intérêt de pouvoir donner lieu à des « calculs », disons plutôt des opérations sur les évaluations obtenues.
Ainsi, nous verrons que, dans le cadre du traitement des données recueillies par le décideur, la méthode « Satisfaction-Regret », par exemple, utilisera les évaluations obtenues par les différents critères à prendre en compte (l’évaluation des critères d’une zone sera donc de la forme : « la zone dispose du critère X : assez vrai », ceci pour chacun des critères) afin d’évaluer un ou plusieurs « aspects » de la zone (nous avons précisé dans le chapitre précédent ce que l’on entendait par « aspect »). La prise de décision sera alors plus facile.
Cette échelle de vérité intervenant donc logiquement à la fois dans l’évaluation des critères et dans le traitement des données, nous ne présenterons dans ce paragraphe que les opérateurs et leur fonctionnement. La méthode « Satisfaction-Regret » sera, elle, exposée dans la section suivante axée sur l’aide multicritère à la décision.
3.2.2. Calcul sur des propositions floues
La négation « * ».
Si la proposition « z possède une faible population » obtient dans l’intervalle [0;1] une valeur comme, par exemple, pop (z) = 0,25 ; alors, le niveau de vérité de sa négation : « z ne possède pas une faible population » sera pop*(z)=1-pop(z)=0,75. Dans le cadre de l’échelle de vérité de Bernard Fustier, la négation d’une proposition est donnée par l’échelon opposé :
Si :_ pop(z) = vrai,alorspop*(z) = faux
Si :_ pop(z) = assez faux,alorspop*(z) = assez vrai
Conjonction, disjonction
Considérons une seconde proposition, « z est verdoyante » dont le niveau de vérité est noté v(z). Les opérateurs de conjonction (« min ») et de disjonction (« max ») généralement utilisés dans le cas numérique [0;1] sont directement transposables au cas de l’échelle de Fustier :
Conjonction « » :
« z possède une faible population ET z est verdoyante » sera définie par min[pop(z),v(z)], par exemple si pop(z)=assez vrai et v(z)=presque faux, alors min[pop(z),v(z)]=presque faux.
Disjonction « » :
« z possède une faible population OU z est verdoyante » sera définie par max[pop(z),v(z)], par exemple si pop(z)=assez vrai et v(z)=presque faux, alors max[pop(z),v(z)]=assez vrai.
On dira qu’ici le OU est inclusif, il ne signifie pas « soit l’un, soit l’autre » mais « l’un ou bien l’autre ou bien les deux » (au moins l’un des deux).
Certains résultats paraissent parfois surprenants. En effet, prenons le cas où :
v(z) = assez vrai, alors v*(z) = assez faux, aussi :
[ v(z) v*(z) ] = min[ v(z) , v*(z) ] = assez faux.
Ce qui signifie qu’à la proposition « z est verdoyante ET z n’est pas verdoyante », alors que l’on répondrait intuitivement faux (comme le fait la logique booléenne) si l’on estime qu’une zone ne peut pas à la fois être et ne pas être verdoyante, les opérateurs utilisés donnent (seulement) : assez faux. Il faudra en déduire qu’il est possible que z soit globalement verdoyante avec ici et là quelques parcelles non verdoyantes. Ce résultat vient bousculer le principe de non-contradiction de la logique booléenne.
Le principe du tiers exclu de la logique booléenne qui veut qu’une proposition soit : soit vraie, soit fausse et par conséquent qu’à une proposition combinée du type « z est verdoyante OU z n’est pas verdoyante » on réponde forcément vrai est également remis en cause.
En effet, reprenant les valeurs précédentes, à la proposition « v(z)v*(z) » on répond (seulement) : max[v(z),v*(z)] soit : assez vrai. Cas d’une zone globalement verdoyante et partiellement non-verdoyante.
Evidemment dans le cas d’une proposition « complètement » vrai ou complètement fausse, ces deux principes ne pourront être que respectés et ils le seront puisque :
v(z) = vrai v*(z) = faux aussi : [v(z)v*(z)] = min[v(z),v*(z)] = faux.
de même que : [v(z)v*(z)] = max[v(z),v*(z)] = vrai.
3.2.3. Application au critère de ruralité
L’exemple très simple qui suit n’est présenté qu’à titre indicatif, il propose de façon similaire de déterminer le niveau de vérité de la proposition « z est une zone rurale » ; pour cela on prendra en compte les niveaux de vérité obtenus par les différents lieux (ou parcelles constituant la zone z) lors de l’évaluation de leur (faible) population et de leur « verdoyance ». Ces résultats peuvent être représentés simultanément dans un tableau du style :
| Ensemble des lieux à faible population de z | ||
| pop(z) | partie de z considérée | v(z) |
| vrai | a | faux |
| presque vrai | b | à moitié vrai |
| faux | c | assez faux |
| assez vrai | d | assez vrai |
| Ensemble des parcelles verdoyantes de z |
C’est en combinant les résultats concernant la population et la « verdoyance » que l’on pourra évaluer la ruralité la zone z ou plus précisément les niveaux de ruralité des lieux constituant cette zone. Deux principes peuvent être retenus à cet effet.
_On pourra estimer de façon relativement sévère qu’un lieu est (plus ou moins) rural s’il possède à la fois (plus ou moins) les deux caractéristiques. C’est donc l’opérateur « » (ET) qui sera utilisé, donnant ainsi un niveau de vérité à la proposition « le lieu possède une faible population ET le lieu est verdoyant » équivalent à [pop(z)v(z)]=min[pop(z),v(z)]. Résultat que l’on pourra noter R(z).
Dans un même tableau, semblable au précédent, les résultats ainsi obtenus feront ressortir les lieux n’appartenant pas ou appartenant (plus ou moins ) à l’espace rural de z :
| Espace rural de z | ||
| R(z) = min[pop(z),v(z)] | partie de z considérée | R*(z) = opposé de R(z) |
| faux | a | vrai |
| à moitié vrai | b | à moitié vrai |
| faux | c | vrai |
| assez vrai | d | assez faux |
| Espace non rural de z |
Dans cet exemple, les parcelles a et c sont totalement exclues de l’espace rural et appartiennent totalement à l’espace non rural. Tandis que b appartient en partie à l’espace rural et en partie au non rural de façon très nuancée. Enfin, on voit que d est assez rural, il semble donc naturel qu’il appartienne tout de même un peu à l’espace non rural.
_En étant quelque peu plus souple, on aurait tout aussi bien pu considérer qu’un lieu appartiendrait à l’espace rural s’il disposait de l’une OU de l’autre des caractéristiques considérées.
Ce qui signifierait que l’on estime qu’une zone est rurale si elle dispose d’une faible population ou si elle est verdoyante. Dans ce cas, c’est l’opérateur « » (OU) qui sera employé pour donner un niveau de vérité à la proposition « le lieu possède une faible population OU le lieu est verdoyant » équivalent à [pop(z) v(z)]=max[pop(z),v(z)]. Résultat que l’on notera toujours R(z).
L’espace rural de la zone z devient alors :
| Espace rural de z | ||
| R(z) = max[pop(z),v(z)] | partie de z considérée | R*(z) = opposé de R(z) |
| vrai | a | faux |
| presque vrai | b | presque faux |
| assez faux | c | assez vrai |
| assez vrai | d | assez faux |
| Espace non rural de z |
Dans cet exemple simple, on arrive à déterminer les niveaux de ruralité des différentes parcelles de la zone z. Ces parcelles, ou lieux, pourront être regroupées (cartographiquement) et, pourquoi pas, colorisées pour faire ressortir visuellement les différents degrés de ruralité de la zone z et par la même sont niveau global de ruralité.
3.2.4. Principes de synthèses des évaluations
En règle générale, les opinions des experts sont obtenues comme suit :
Dans un premier temps, on appréciera le niveau d’adéquation de chaque objet à chaque propriété, puis, on appréciera l’importance relative de chaque propriété dans le problème d’évaluation. Ces évaluations sont réalisées par des experts selon deux cas :
- Les évaluations sont attribuées collectivement : Les experts entament un dialogue sur le choix de chaque niveau de vérité (nous verrons que c’est l’échelle de vérité verbale, déjà présentée, qui est utilisée dans cette méthode).
Lorsqu’un désaccord semble partager durablement les participants, on retient le niveau de vérité médian comme réponse du groupe. Les réponses extrêmes sont réintroduites après coup dans le modèle en vue d’analyser leurs effets sur une éventuelle modification des résultats.
- Les évaluations sont attribuées individuellement : Les experts sont interrogés séparément, la synthèse des évaluations s’effectue en deux temps :
– Synthèse des évaluations par expert :
– Synthèse des évaluations globales des experts :
Où (1) … (N) représentent le niveau de compétence que chaque expert s’attribue en fonction de la connaissance qu’il possède du problème. Comme les pondérations des points de vue, les niveaux de compétence sont choisis le long de l’échelle d’évaluation verbale. Les évaluations globales permettent d’obtenir un « classement » des objets en fonction de l’objectif général.
Ce système d’évaluation présente de nombreux avantages, à commencer par le fait qu’il prend en considération les critères qualitatifs au même titre que les critères quantifiables, puisque l’évaluation verbale permet de les comparer, de les traiter ensemble, grâce aux opérateurs dont il dispose. Cette particularité de la méthode n’est pas négligeable ; il sera en effet intéressant de pouvoir confronter lors de l’évaluation un critère que l’on qualifiera d’écologique à un critère disons financier.
Notons également que le principe de l’évaluation selon l’échelle de vérité de Fustier facilite grandement l’estimation des différents éléments à traiter.
Conclusion
Nous l’avons suffisamment souligné, l’évaluation des zones est une phase essentielle de la mise en oeuvre de la stratégie de développement proposée dans cette étude. L’implantation de telle ou telle structure touristique, la mise en valeur ou la sauvegarde d’un périmètre, le choix d’une exploitation agricole plutôt que touristique sur une zone, toutes ces décisions qui permettront au territoire dans son ensemble de bénéficier de l’effet de la spécialisation microrégionale que nous avons montré, seront fondées sur les caractéristiques propres à chacune des zones répertoriées.
Cependant, les principales caractéristiques que l’on devra prendre en compte pour tirer de telles conclusions quant à l’avenir économique des différentes zones peuvent-elles être réunies en un critère unique qu’il suffirait alors de considérer pour établir un plan d’orientation ? Evidemment non.
Toutefois, il semblerait que la principale notion à prendre en compte dans le cadre du développement touristique d’une zone selon les remarques et démonstrations avancées jusqu’ici pourrait se résumer (pour faciliter la mise en oeuvre d’un exemple concret) dans la notion de « sensibilité ». La connaissance du degré de sensibilité d’une zone nous informerait sur la possibilité d’y exploiter tel produit touristique plutôt que tel autre, ou carrément sur l’intérêt de la préserver de toute dégradation éventuelle.
Encore faut-il s’entendre sur le terme « sensibilité ». Si l’on trouve dans la littérature spécialisée les notions « d’espaces naturels sensibles » (Bourgoin-Bareilles, 1998), de « périmètres sensibles » (Toulemonde, 1978) ou encore de « zones sensibles » (Prieur, 1996), on se rend bien compte qu’il n’existe pas de définition empirique de la sensibilité et que celles qui sont proposées ici ou là sont évidemment fonction du domaine traité.
Ainsi devrions nous proposer notre propre notion de sensibilité qui serait cette fois relative à la prédisposition (ou non) à un éventuel développement touristique et de quel type. La tâche parait ambitieuse mais néanmoins réalisable.