Les modèles mathématiques d’épargne financière

Les modèles mathématiques d’épargne financière

Chapitre III:

Les modèles mathématiques d’épargne financière

(19)(20)(21)(22)(23)

III.1. Définitions et notations

On définit la valeur actuelle VA > 0 d’une épargne financière observée dans le temps (t), un montant d’argent déposé ou crédité par un individu et/ou un manage (créancier).

On définit aussi le taux d’intérêt (i) sur une période comprise dans l’intervalle de temps [1; +∞], des entiers naturels non nuls.

Le taux d’intérêt (i) et le temps (t) sont des variables qui occasionnent les gains sur un montant déposé en banque ou à un débiteur au cours de la période concernée.

L’épargne financière est la variable d’intérêt dans le contexte de la modélisation financière.

On associe à la valeur future VF(t) : le temps (t), la valeur actuelle (VA) et le taux d’intérêt (i) fixe ou aléatoire dépendamment d’un débiteur ou d’une banque.

Alors la valeur future VF(t) peut être représentée de la manière suivante :

III.1.1 L’utilisation de modèles en finance

On doit considérer les implications de l’utilisation de modèles en finance avant d’entreprendre leur étude. On doit aussi prendre connaissance des différents types ainsi que les risques liés chacun d’entre eux.

Pour ce faire, on se réfère à la note «Model Risk» publiée par Derman (1996).

Durant les dernières décennies, plusieurs modèles sont apparus afin de fournir une approche fondamentale aux concepts de tarification, d’offre et de demande et d’arbitrage aux intervenants des milieux financiers.

Au cours des années 1970, on se préoccupe particulièrement des fluctuations des taux d’intérêt, un phénomène qui marque cette époque.

Les notions de duration et de convexité font alors leurs débuts.

Sur les marchés de capitaux propres, on s’intéresse à la discordance entre le prix négocié des contrats à terme et le prix raisonnable calculé selon une perspective théorique.

19 F. Pelletier (2014), Modélisation des rendements financiers à l’aide de la distribution de Laplace asymétrique généralisée, LAVAL, Québec-Canada

20 BORGNE, H. (2012), Calculs bancaires, ISBN : Paris, Vol : 39.

21 Bachelier (L.), (1900), Théorie de la spéculation, Ann. Sci. École Norm. Sup., Paris, Vol : 112.

22 Lamberton D., Lapeyre, B. (1991), Introduction au calcul stochastique en Finance, Collection Mathématiques et Applications 9 Belgique, Vol : 65

23 MAGALI, K. (2009), Etude des modelés non domines en mathématiques financières, HAL : Université d’Evry-Val d’Essonne, France, Vol : 149.

Puis, la confiance développée envers le modèle de tarification d’options de Black et Scholes (1973) et ses extensions a favorisé la croissance du marché des produits dérivés.

La puissance de calcul croissante des ordinateurs a aussi permis l’élaboration et l’utilisation de modèles de plus en plus sophistiqués.

La dépendance qui peut se développer envers ceux-ci apporte son lot de considérations. On doit donc se rappeler l’utilisation désirée par les auteurs de ceux-ci et le risque associé à leur usage à grande échelle.

III.1.2 Différents types de modèles mathématiques d’épargne financière

Toujours selon Derman, un modèle financier peut être classé parmi au moins trois catégories :

1. Le modèle fondamental, basé sur un système de postulats et de données, entre lesquels on peut établir différents relations. Le modèle de Black- Scholes en est un exemple.
2. Le modèle phénoménologique, qui présente une description ou une analogie, afin d’illustrer quelque chose qui ne peut être directement observé.

C’est un modèle moins fondamental, basé aussi sur des liens de cause.

Un modèle qui chercherait à expliquer l’impact du retrait du porteur de parts majoritaire d’une entreprise sur la valeur des actions de celle-ci serait phénoménologique.

3. Le modèle statistique, basé sur une régression ou un réglage optimal entre différents ensembles de données. On ne cherche pas ici à expliquer une dynamique, mais à décrire une tendance ou une corrélation.

Le modèle d’évaluation des actifs financiers en sont des exemples.

Un modèle financier est en partie basé sur des variables qui représentent des opinions et des anticipations, et non seulement des quantités mesurables. Ces variables peuvent être, entre autres, le rendement et la volatilité future espérés.

Cette considération sera importante notamment lorsque l’on voudra déterminer le prix raisonnable d’un produit dérivé.

En effet, un modèle de tarification est essentiellement un moyen de refléter l’intuition des acteurs du marché à propos de ces variables sous la forme d’un prix exprimé dans une unité monétaire.

Un bon modèle doit faciliter l’extrapolation de ce prix sous certaines conditions de marché.

Contrairement à la physique classique, un principe fondamental en finance est l’incertitude. On ne peut anticiper la valeur d’un titre à un moment donné dans le futur avec la même précision qu’on peut prévoir la position d’un objet à cet instant.

Les outils mathématiques principalement utilisés seront alors les processus stochastiques, les statistiques et les distributions de probabilités, en plus du calcul différentiel et intégral.

III.1.3 Le risque de modélisation

Plusieurs risques inhérents à la modélisation en finance existent. Quelques-uns d’entre eux seront décrits dans cette section. La modélisation peut tout simplement ne pas être applicable à la situation étudiée.

L’exemple le plus probant serait de tenter de prévoir les mouvements du prix d’un titre financier à court terme.

Un modèle peut être incorrect pour plusieurs raisons. Entre autres, il peut ignorer certains facteurs ou poser une hypothèse déterministe inappropriée sur ceux-ci.

Il peut aussi considérer une dynamique incorrecte pour un des facteurs ou encore une relation inappropriée entre ceux-ci.

Enfin, il peut n’être applicable que sous certaines conditions bien précises ou encore que son utilisation soit limitée à court terme, notamment lorsqu’il nécessite un temps de calibration pour être statistiquement valable.

Il peut aussi être inutilisable par une mauvaise estimation des paramètres.

Un modèle peut aussi être correct, mais avoir une solution erronée. Cela se produit notamment lorsqu’on tente de dériver une solution analytique ou que l’on doit utiliser des méthodes numériques pour obtenir celle-ci.

On se doit, dans ce cas, de connaître l’erreur maximale possible de la méthode utilisée. Un modèle correct peut aussi être utilisé dans le mauvais contexte.

Par exemple, on pourrait avoir recours à des paramètres inadéquats de simulation, ou encore réutiliser le modèle dans une autre situation sans tenir compte des conditions de validité de celui-ci.

Son utilisation peut générer des prix déraisonnables; on parle alors d’arbitrage de modèle.

Par exemple, si un titre est évalué à l’aide du modèle d’évaluation des actifs financiers, son prix sera diifférent de celui qui serait obtenu avec la régression à trois facteurs de Fama et French.

Un investisseur peut alors faire du profit en achetant le titre à celui qui demande le prix le plus faible pour le revendre à celui qui offre le plus élevé.

L’utilisation de données instables peut produire des résultats différents selon la période étudiée. La possibilité qu’une estimation basée sur des données historiques soit erronée doit être considérée.

Enfin, comme la plupart des modèles financiers sont implémentés sous forme de logiciels, différents bogues informatiques peuvent se retrouver dans le code source.

On considère entre autres des erreurs d’arrondissement, de logique et de clarté du code, ainsi que des particularités du matériel qui n’auraient pas été prises en compte par le programmeur.

Ces erreurs peuvent être difficiles à détecter, c’est pourquoi un grand nombre de tests devraient être effectués avant de publier un logiciel de modélisation financière.

III.1.4 Les rendements financiers

Le rendement est défini comme étant le gain ou la perte de valeur d’un actif sur une période donnée. Il est constitué des revenus occasionnés et des gains en capitaux d’un investissement et est habituellement représenté sous la forme d’un pourcentage.

Ces derniers peuvent prendre la forme de coupons pour les titres à revenus fixes et de dividendes pour les actions échangées sur les marchés boursiers.

On ne considèrera, dans ce texte, que les titres boursiers sans dividende, dont le rendement est lié uniquement aux gains en capitaux.

III.2 Les suites

En modélisation financière, une suite est une série de versements que se fixent le débiteur et le créditeur sous forme des amortissements moyennant le temps.

La suite a pour objet soit de rembourser une dette, soit de constituer un capital, le terme « suite » est habituellement réservé à des périodicités; lorsque la période est d’une année; on l’appelle «annuité » c’est comme-cela qu’on peut l’appeler « semestrialité », « trimestrialité »ou « mensualité ».

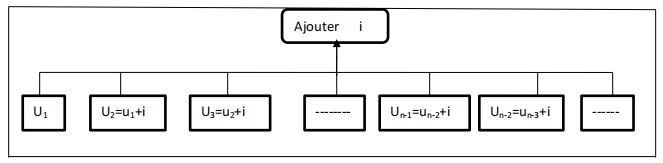
La suite utilisée ici est une suite arithmétique de premier terme u1 et de raison i.

P = u₁ x u₂ x u₃ x…………+u_nse note aussiP = ^𝑛. 𝑢_k
𝑘=1
P = u₁ x u₂ x u₃ x…………+u_nse note aussiP = ^𝑛. 𝑢_k

Dans ce cas, c’est une suite géométrique qui est une suite de nombres tels que pour passer d’un terme à son suivant on multiplie toujours la même quantité appelée raison (i) par le premier terme u1 jusqu’à un.

Cette notion des suites est la problématique de la théorie de l’optimisation de portefeuilles financiers, elle est très utilisée en fiscalité.

Dans plusieurs manuels, la raison de la suite arithmétique est notée par r et celle de la suite géométrique par q mais ici on modélise le tout par i.

Evoqué plus haut, l’utilisation des suites et séries mathématiques en finance n’est que des versements d’argents fixés par le débiteur et le créditeur qu’on préfère représenter par i pour expliquer qu’en réalité, les versements dépendent du taux d’intérêts (i).

III.3 Les opérations d’épargnes

III.3.1 Accumulation du capital

En finance du marché et de l’entreprise, l’accumulation du capital est le processus qui est lié à l’investissement financé par l’excédent brut d’exploitation ou par l’emprunt.

Comme le capital subit une dépréciation permanente du fait de son utilisation pour la production, il y a accroissement du capital et donc accumulation si l’investissement brut est supérieur à cette dépréciation.

VF(t) = VA x (1 + i) t

Légende :

• VF(t)=valeur future avec le temps
• VA= valeur actuelle
• i =taux d’intérêts
• t = temps en période

III.3.2 Actualisation du capital

L’actualisation est l’opération inverse de la capitalisation. L’actualisation permet de ramener à une date antérieure un capital futur.

Actualiser un capital, c’est trouvé la valeur actuelle (VA), c’est par exemple répondre à la question suivante : « de quel capital devrais-je disposer aujourd’hui pour obtenir à la date t période, un capital de 1 FC, sachant que le taux d’intérêt i est constant ? ».

𝐕𝐀 𝐕𝐅𝒕 (𝟏 𝒊)𝒕

Légende :

• VA=valeur actuelle nette
• i= taux d’intérêts constant
• t=temps en période

III.4 Notions générales et Intérêts (rentabilité financière)

III.4.1. Deux notions fondamentales : intérêt et taux d’intérêt

III.4.1.1 La notion d’intérêt

Il s’agit de la somme due par l’emprunteur au prêteur ou reçue de l’emprunteur par le prêteur en plus du capital prêté symbolisé par I majuscule.

Exemples :

Monsieur X emprunte 12 000 FC à sa banque pour l’achat d’une automobile. Il rembourse ce prêt en faisant 36 paiements mensuels de 365 FC. Un calcul rapide permet de déterminer que l’intérêt versé est 36 × 365 − 12 000 = 1 140 FC.

Madame X place 4 500 FC pour 3 ans. Au bout des 3 années, son capital est de 5 445 FC. L’intérêt versé à Madame X est donc : 5 445 – 4 500 = 945 F.

III.4.1.2 La notion de taux d’intérêt

Le taux d’intérêt mesure la rémunération d’un prêteur ou d’un investisseur qui se sépare temporairement d’une unité monétaire pendant une période.

Il s’exprime en général sous forme de pourcentage des sommes prêtées ou placées par période qui est symbolisé par i minuscule.

Exemple :

• Un taux annuel de 6% signifie que pour 1 FC emprunté, il sera remboursé 1,06 FC au bout d’un an.

Par ailleurs, il est possible de classer les taux d’intérêt dans différentes catégories :

Taux fixes/Taux variable

Le taux fixes désigne un taux d’intérêt fixé lors de la signature du contrat. Il ne variera pas, quoi qu’il arrive et le taux variable désigne un taux non définitivement fixé, qui évolue à la hausse comme à la baisse.

Taux nominal / Taux réel

Le taux nominal est le taux d’intérêt qui est fixé lors de l’opération d’emprunt ou de prêt. Il est inscrit dans le contrat qui lie emprunteur et prêteur et sert à calculer les intérêts dus.

Le taux réel est le taux nominal après déduction du taux de l’inflation.

Cette définition n’est valable que si le taux d’inflation est faible, sinon il faut utiliser l’équation : 1 + taux d’intérêt nominal = (1 + taux d’intérêt réel) x (1 + taux d’inflation).

En période de forte inflation (par exemple durant les « Trente glorieuses »), les taux d’intérêt réel peuvent être négatifs, ce qui incite à emprunter.

III.4.2 Intérêts simples

III.4.2.1 Définition

• Un intérêt I est dit simple lorsqu’il est payé en une seule fois et proportionnel à la durée du placement.
• Il est fonction de :
  • i : taux d’intérêts,
  • t : la durée du placement,
  • C : le capital

III.4.2.2 Notation

𝐼 𝐶 𝑥 𝑖 𝑥 𝑡

Attention : Il faut toujours exprimer i et t en unité de temps comparable. Par exemple i annuel et t en année, ou i mensuel et t en mois.

III.4.2.3 Le taux d’intérêt (i)

Le taux d’intérêt est l’intérêt payé (ou rapporté) par période de prêt (ou le placement) d’un capital.

Dans la pratique, ce taux est généralement exprimé en pourcentage (i = x %) et pour une période annuelle, trimestrielle, semestrielle et mensuelle.

III.4.2.3.1 La durée (t)

Cette donnée obéit à des conventions précises mais évolutives en fonction du type de prêt ou de placement.

Il est donc nécessaire de toujours se faire préciser quelles sont les conventions adoptées si l’on veut avoir une idée précise de ce que représente véritablement le taux d’intérêt d’une opération.

Attention : le t se calcul proportionnellement à la Base (B) et aux modalités de paiement fixé dans le contrat qui s’expriment en nombre de jours du prêt (n).

𝑡 = 𝑛 /𝐵

• La Base : Les cas les plus fréquents sont :
  1. Base = 360 : on parle de base commerciale (année bancaire)
  2. Base = 365 ou 366 : on parle de base exacte2.
• Le nombre de jours de prêt : Il obéit aussi à des conventions.
• Dans le cadre d’une base en jours exacts, ce nombre de jours correspond en général au nombre de jours « exact »
• Dans le cadre d’une base 360, deux modes sont utilisés, le précédent ou le calcul dit « en mois » On considère que l’année de 360 jours se décompose en 12 mois de 30 jours.

Quels que soient les mois considérés, n mois représentent (30 = n) jours. Ce mode de calcul est surtout utilisé dans le cas de remboursement par échéances constantes.

III.4.3. Intérêts composés

III.4.3.1 Définition

• Un capital est placé à intérêts composés quand, à la fin de la période (dite période de capitalisation), les intérêts sont rajoutés au capital pour porter eux-mêmes intérêts pour la période suivante…
• C’est donc une application des suites et séries mathématiques.

Il est fonction de :

• • • Ct= valeur acquise
    • C = capital
    • i = taux d’intérêts périodique
    • t = durée du placement

III.4.3.2 Notation

C_t = C₀ X (1+i) ^t

III.4.3.3 Taux de Rendement Annuel Arithmétique

Taux permettant de calculer la quantité d’intérêts de l’opération, soit :

TRAA x N (C0) − 𝐵 (𝐶1 − 𝐶0) = 0

III.4.3.4 Taux de rendement actuariel (Taux équivalents)

• Définition : Deux taux sont dits équivalents s’ils génèrent, pour un capital et une durée donnée mais des périodes de capitalisation qui peuvent être différentes, un même taux d’intérêt.
• Taux équivalent annuel : Le plus souvent on calcule le taux actuariel annuel correspondant au taux mensuel, trimestriel…

Tact = (1 + i) ^t -1

Légende :

• i : taux d’intérêts périodique
• Tact= taux actuariel annuel
• t : la durée de périodes

Cas général :

C₀ x (1 + i mensuel) ¹²= C₀ x (1 + i trimestre) ⁴ = C₀ X (1 + i annuel) ¹=…..

III.4.4. L’escompte simple

III.4.4.1 Par définition

L’escompte est une forme très particulière de prêt. Il s’agit en réalité de la négociation de promesses de paiement ou traites (ou encore lettres de change) avant leur échéance.

L’organisme financier qui acquiert les promesses de paiement les règles comptant mais retient un certain intérêt que l’on appelle l’escompte.

La théorie de l’intérêt simple permet aisément de calculer cet intérêt.

La seule différence est que le capital à prendre en considération n’est pas le capital présent, ou la valeur actuelle de la traite, mais bien son nominal, sa valeur future.

III.4.4.2 Notation

E = 𝐶𝑡 x t x i

Ct représente la valeur nominale de la traite à négocier, donc sa valeur future; t représente sa durée. Généralement l’unité choisie est l’année; dans ce cas, si n est un nombre de jours, il sera exprimé en 1/360.

Le symbole i représente le coefficient de proportionnalité utilisé et porte le nom de taux d’escompte.

III.4.5 L’escompte commercial

L’escompte d’effets de commerce (lettres de change ou « traite », billets à ordre) consiste en une cession d’une créance à un établissement bancaire, cession qui sera opposable aux autres créanciers en cas d’ouverture d’une procédure collective.

Afin de bénéficier de cette possibilité, l’entreprise doit négocier avec ses banques des lignes d’escompte qui déterminent, pour chaque établissement, le montant maximum d’escompte autorisé.

Ces lignes sont attribuées en fonction de l’activité, du risque global de l’entreprise, de la nature de son crédit client (durées de règlement, modes de règlement, risques), …

Procédure : l’entreprise remet à sa banque un bordereau accompagné des effets cédés; la banque, après vérification, crédite le compte de l’entreprise du montant de la remise diminué des frais facturés.

Si les effets ne sont pas impayés, l’opération est alors achevée. Sinon la banque débitera, après l’échéance, le compte de l’entreprise du montant des impayés.

Le coût de l’escompte se décompose en 2 parties : les agios et les commissions.

• Les agios sont calculés en fonction du montant de la remise, de la durée de chaque effet et du taux d’intérêt appliqué par la banque à l’entreprise. Par ailleurs les agios sont calculés sur la base d’une année de 360 jours.

Ainsi, par exemple, si le taux facturé est de 30 %, pour une durée de 30 jours et un effet de 10.000 FC, les agios s’élèvent à : 10.000 x 30 x (0,12 / 360) = 100 FC.

• Aux agios, s’ajoutent diverses commissions : commission de service dont le montant dépend du support utilisé (le papier est plus onéreux que le magnétique) et, éventuellement, commission d’acceptation.

Ces commissions sont soumises à la TVA.

E_C = C_t x i x t

Il n’est pas rare que les banques facturent un montant minimum forfaitaire d’agios par effet, afin de décourager les opérations portant sur des montants unitaires trop petits.

Légende :

• EC= Escompte commercial
• i = taux d’escompte
• t = la durée de l’échéance

III.4.6. La Valeur Actuelle Nette (VAN) d’un investissement

III.4.6.1 Définition

La Valeur Actuelle Nette (VAN) d’un investissement est la différence entre les cash-flows (flux) actualisés à la date t0 et le capital investi I.

Ou

VAN = C₁ (1+i)^-1 + C₂ (2+i)^-2 + C₃ (3+i)^-3 +…C_N (n+i)^-n–I

Remarque : On écrit souvent VAN(i) au lieu de VAN pour montrer qu’elle dépend du taux i choisi

III.4.6.2 Taux d’actualisation

Le taux d’actualisation utilisé dans le calcul de la VAN est le taux de rentabilité minimum exigé par l’entreprise.

III.4.7. Indice de profitabilité (IP)

III.4.7.1 Définition

L’indice de profitabilité (IP) est le quotient de la somme des cash-flows (flux) actualisés par le montant du capital investi I.

4.7.2 Lien entre IP et VAN

Démonstration :

• VAN = ( .Ct (1+i)-t)-i
• Donc VAN + I = .Ct (1+i)-t
• Soit en divisant tout par I : 1 .Ct (1+i)-t = = +1

III.5. La Théorie des Options

Les contrats d’options font partie de ces produits qui se sont amplement multipliés ces dernières années sur les marchés financiers.

Concrètement les innovations, élaborées grâce aux techniques utilisées dans les bourses de commerce et sur les marchés à terme de marchandises ou de matières premières, ont porté sur la création de marchés à terme de contrats de devises et de taux d’intérêts par exemple.

Les contrats d’options ne sont finalement qu’une variété ou encore une extension des contrats à terme; toutefois leurs marchés ont pris une extension considérable.

Les options sont des actifs financiers qui permettent un arbitrage particulier entre la rentabilité et le risque.

Au sens strict, un contrat d’option sur actions donne le droit à son détenteur d’acheter (option d’achat ou «call ») ou de vendre (option de vente ou «put ») ultérieurement une ou plusieurs actions à un prix déterminé à l’avance; ce type de contrat est «valorisé » sur le marché financier.

Les options (que l’on appelle encore « actifs conditionnels ») peuvent prendre des formes multiples; outrent qu’elles sont d’achat ou de vente, on distingue également les options de deux autres manières.

III.5.1 Les modèles d’évaluation des Options

On reconnaît principalement trois modèles d’évaluation des options sur actions; le 3ème modèle est en réalité une extension du modèle de BLACK & SCHOLES (prise en compte des dividendes omis par le modèle initial).

• L’approche binomiale (COX, ROSS & RUBINSTEIN, 1979) : principes, duplication (« spanning »), treillis binomial
• Le modèle de BLACK et SCHOLES (1973) : technique de la diffusion.
• Autres modèles d’évaluation : variantes et prolongement du modèle de diffusion (WIENER, MERTON, COX & ROSS, RUBINSTEIN); prise en compte du paiement d’un dividende (BLACK)

III.5.2. Le modèle de BLACK et SCHOLES

En1973, Black et Scholes ont proposé une formule, qui porte aujourd’hui leurs noms, pour le prix d’une option. Cette formule est très utilisée en pratique à tel point que la volatilité implicite qu’elle est devenue une véritable unité de mesure.

Le modèle mathématique qui décrit le marché financier est à la fois simple et efficace, selon les hypothèses du modèle de Black-Scholes, cette technique permet d’assurer le gérant contre la baisse de ses fonds.

Ce modèle de BLACK & SCHOLES reconnaît 5 paramètres pour l’évaluation des options qui sont :

1. Le prix d’exercice
2. Le prix au comptant (premium)
3. La volatilité du cours de l’action
4. Le taux d’intérêt sans risque (supposé constant)
5. La date d’exercice de l’option

call S xN (d1) − k^{(−r x T)}x N (d2)

Notation : La formule de BLACK & SCHOLES qui donne la valeur d’une option d’achat (call) sur une option est la suivante :

Avec :

S	Le prix de l’action
K	Le prix d’exercice ou « Strike de l’option »
T	La durée de l’option jusqu’à l’échéance
N	La valeur de la distribution normale cumulée
R	Le taux d’intérêt sans risque
d	L’estimation de l’écart-type du taux de rendement du titre
δ	La volatilité implicite de l’option

III.5.2.1 Calcul de δ

On l’estime généralement sur base de la série des cours historiques en calculant le rendement rt = ln (Ct) – ln (Ct-1) et en déterminant l’écart-type de cette série.

III.5.2.2 Calcul de d

Remarque :

• Dans de nombreuses présentations, on trouve d2 = (d1 – δ. ϒT)
• La valeur de l’option de vente (put) s’obtient par la formule :

Put K^{(−r x T)}x N(−d2) − S x N(−d1)

III.6. Présentation de quelques algorithmes appliqués

III.6.1 Algorithme PAWELOLE de capitalisation

Algo-PAWELOELE de capitalisation Var VF, i, VA : Réel
Tableau X1[1, t] : Entier Début
Ecrire (« Entrer le nombre d’échéance : t « ) Lire t
Pour VF=VA* (1+i) jusqu’à t Ecrire ( » Itération « , VF) Pour i = 1 jusqu’à n
Pour j = 1 jusqu’à n
Pour t =1 jusqu’à n
XX1 [i, j] = VFVF11+ (G [i, t] * X1[t, j]) VFVF11=XX1 [i][j]
t suivant VFVF11=1;
XX1 [i][j] = XX1[i][j] + c[i][j];

• Affichage de valeur future

Pour j = 1 jusqu’à n Ecrire XX1 [i, j]
Pour i = 1 jusqu’à n
Pour j = 1 jusqu’à n X1[i, j] = XX1 [i, j]
j suivant i suivant
k suivant
Fin

III.6.2 Algorithme PAWELOLE d’actualisation Algo-PAWELOELE d’actualisation

Var VF, i, VA : Réel Tableau X1[1, t] : Entier Début
Ecrire (« Entrer le nombre d’échéance : t « ) Lire t
Pour VA=VF * 1/ (1+i) jusqu’à t Ecrire ( » Itération « , VF) Pour i = 1 jusqu’à n
Pour j = 1 jusqu’à n
Pour t =1 jusqu’à n
XX1 [i, j] = VFVF11+ (G [i, t] * X1[t, j]) VFVF11=XX1 [i][j]
t suivant VFVF11=1;
XX1 [i][j] = XX1[i][j] + c[i][j];

• Affichage de valeur actuelle

Pour j = 1 jusqu’à n Ecrire XX1 [i, j]
Pour i = 1 jusqu’à n
Pour j = 1 jusqu’à n X1[i, j] = XX1 [i, j]
j suivant i suivant
k suivant
Fin