4.4 Logique temporelle linéaire LTL
Nous présentons dans cette section une logique temporelle linéaire (LTL). Cette présentation nous permet d’introduire une variante de cette logique, PP-LTL (Pure Past Linear Temporal Logic) qui est dédiée aux faits passés. Une présentation plus détaillée peut être trouvée dans [57].
Une logique temporelle est une extension de la logique conventionnelle : elle intègre de nouveaux opérateurs qui expriment la notion du temps. La logique classique ne peut pas exprimer une assertion liée au comportement d’un système par exemple, « après exécution d’une instruction I, le système se bloque ».
Dans une telle assertion, les actions s’exécutent en suivant l’axe du temps : à l’instant t l’instruction I est exécutée et à l’instant t+1 le système est bloqué. Les logiques temporelles ont été proposées pour modéliser ce type d’assertion, en fournissant des opérateurs pour exprimer les comportements passés et futurs du système.
La logique LTL permet de représenter le comportement des systèmes réactifs au moyen de propriétés. Les propriétés spécifient le comportement du système à un moment de son exécution.
Le système fonctionne de manière linéaire dans le temps. Les exécutions du système peuvent être modélisées par un système de transition ST qui se compose de plusieurs états, et permet de passer de l’un à l’autre. Chaque état de ST correspond à un état du système à un instant t. À chaque état, nous pouvons observer les propriétés, si elles existent, pour identifier le comportement du système. Le comportement global du système est spécifié par l’observation des propriétés dans tous les états concernés.
L’activité du système se déroule de manière chronologique (figure 4.2). Elle se décompose en une séquence d’états représentant les actions de l’entité dans le temps.
Fig. 4.2 Déroulement temporel d’un système en logique LTL
4.4.1 Syntaxe
Les formules de la logique LTL peuvent être définies de la manière suivante :
-Propositions atomiques :
true | f alse | (x = v) sont des formules ((x = v) se lit x a pour valeur v).
-Connecteurs booléens :
Soit φ, ψ ∈ LT L, toutes les formules de la forme suivante appartiennent à LTL :
¬φ | φ ∧ ψ | φ ∨ ψ | φ → ψ | φ ↔ ψ
-Connecteurs temporels :
Soit φ, ψ ∈ LT L, toutes les formules de la forme suivante appartiennent à LTL :
Gφ | F φ | φ U ψ | X φ
4.4.2 Sémantique
Soit Π = s0, s1, s2 . . ., une séquence d’états du système de transition, et soit φ une formule en logique LTL. On définit « φ est satisfaite pour Π », noté Π |= φ de la manière suivante : pour tout i = 0, 1 . . ., on désigne par Πi la séquence d’états si, si+1 , si+2 . . . (on note que Π = Π0), soit φ et ψ des formules en logique LTL.
1. Π |= true et Π 2 f alse
2. Π |= (x = v) ssi s0 |= (x = v).
3. Π |= φ ∧ ψ ssi Π |= φ et Π |= ψ
Π |= φ ∨ ψ ssi Π |= φ ou Π |= ψ
4. Π |= ¬φ ssi Π 2 φ
5. Π |= φ → ψ ssi Π 2 φ ou Π |= ψ
Π |= φ ↔ ψ ssi Π 2 φ et Π 2 ψ à la fois, ou Π |= φ et Π |= ψ à la fois.
6. Π |= X φ si Π1 |= φ
Π |= F φ si ∃i ∈ (0, 1, . . .) tel que Πi |= φ
Π |= Gφ si ∀i ∈ (0, 1, . . .) tel que Πi |= φ
Π |= φU ψ si ∃k ∈ (0, 1, . . .) tel que j < k, Πj |= φ et j ≥ k, Πj |= ψ
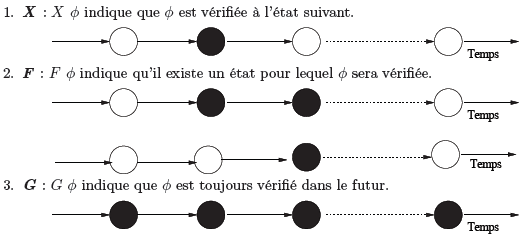
Nous explicitons la sémantique des opérateurs temporels X , F , G et U avec les figures suivantes (les états en noir indiquent que la formule est vérifiée) :
Notons que l’état hachuré indique à partir de quel moment ψ est vérifiée.
Nous pouvons remarquer que la logique LTL est utilisée pour spécifier des faits (le comportement d’une entité) dans le temps (passé et futur). Pourtant, de par les particularités de notre modèle de gestion de la confiance, nous n’avons besoin que d’exprimer des comportements passés. Nous utiliserons donc dans la suite de nos travaux une logique temporelle qui ne s’intéresse qu’aux faits passés : PP-LTL (Pure-Past LTL). Nous présenterons à la section 4.5.3 les détails de PP-LTL.
4.4.3 Exemple
Supposons un système de transactions qui modélise le système téléphonique. Nous avons les deux événements signal et réponse qui représentent la signalisation d’un appel (sonnerie) et l’actions d’y répondre. Pour exprimer le fait que tout signal est suivi d’une réponse, nous pouvons utiliser la formule suivante :
G(signal → F reponse)
4.4.4 Vérification
Les techniques du model checking [17] sont traditionnellement utilisées pour la vérification des formules de logique LTL. Les algorithmes de vérification connus sont NPcomplet.