Modélisation dynamique d’un quadrotor
Modélisation dynamique d’un quadrotor
Introduction
Afin de concevoir un contrôleur de vol, on doit d’abord comprendre profondément la dynamique de l’avion, par conséquent son modèle dynamique.
Cette compréhension est nécessaire non simplement pour la conception du contrôleur, mais aussi pour s’assurer que le comportement de véhicule est plus proche que possible de la réalité lorsque la commande est appliquée.
Le quadrotor est classé dans la catégorie des systèmes volants les plus complexes vu le nombre d’effets physiques qui affectent sa dynamique à savoir les effets aérodynamiques, la gravité, les effets gyroscopiques, les frottements et le moment d’inertie.
Cette complexité résulte essentiellement du fait que l’expression de ces effets diffère pour chaque mode de vol.
En effet les modèles dynamiques du quadrotor proposés changent en fonction des taches planifiées et en fonction des milieux de navigation définis à priori par l’opérateur.
Modèle dynamique du quadrotor
La modélisation des robots volant est une tâche délicate puisque la dynamique du système est fortement non linéaire et pleinement couplée. Afin de pouvoir comprendre au mieux le modèle dynamique développé ci-dessous, voilà les différentes hypothèses de travail :
La structure du quadrotor est supposée rigide et symétrique, ce qui induit que la matrice d’inertie sera supposée diagonale,
Les hélices sont supposées rigides pour pouvoir négliger l’effet de leur déformation lors de la rotation.
Le centre de masse et l’origine du repère lié à la structure coïncident.
Les forces de portance et de traînée sont proportionnelles aux carrés de la vitesse de rotation des rotors, ce qui est une approximation très proche du comportement aérodynamique.
Pour évaluer le modèle mathématique du quadrotor on utilise deux repères, un repère fixe lié à la terre Rb et un autre mobile Rm.
Le passage entre le repère mobile et le repère fixe est donné par une matrice dite matrice de transformation T qui contient l’orientation et la position de repère mobile par rapport au repère fixe.
On choisit la convention d’axes suivants :
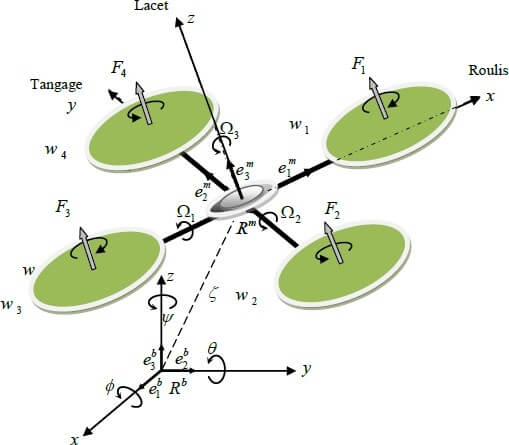
Figure 2.1 : Géométrie du quadrotor.
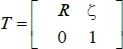
(1)
Avec R la matrice de rotation (décrit l’orientation de l’objet mobile), [𝑥𝑥𝑦𝑦𝑧𝑧] est le vecteur de position. Pour déterminer les éléments de la matrice de rotation R, on utilise les angles d’Euler.
Angle d’Euler
Au début le repère mobile est coïncide avec le repère fixe, après le repère mobile fait un mouvement
de rotation autour de l’axe x d’un angle de roulis�−
𝜋𝜋 2< 𝜙𝜙 <
𝜋𝜋 2�, suivi d’une rotation
Autour de l’axe y d’un angle de tangage�−
𝜋𝜋 2
< 𝜙𝜙 <
𝜋𝜋 2, suivi d’une rotation autour de l’axe z
d’angle de lacet(−𝜋𝜋 < 𝜓𝜓 < 𝜋𝜋). Donc on a la formule de la matrice de rotation R :

Vitesses angulaires
Les vitesses de rotations Ω1, Ω2, Ω3dans le repère fixe sont exprimées en fonction des
vitesses de rotations 𝜙𝜙̇, 𝜃𝜃̇, 𝜓𝜓̇ dans le repère mobile, on a :(II.4)
En effet, la rotation en roulis a lieu lorsque les repères sont encore confondus. Puis, en ce qui concerne le tangage, le vecteur représentant la rotation doit être exprimé dans le repère fixe: il est donc multiplié par 𝑅𝑅𝑅𝑅(𝜙𝜙)−1.
De même, le vecteur représentant la rotation en lacet doit être exprimé dans le repère fixe qui a déjà subites deux rotations.
On arrive ainsi à:
(II.5) (II.6)
Quand le quadrotor fait des petites rotations, on peut faire les approximations suivantes:
c c c 1, et s s s 0.
Donc la vitesse angulaire sera:
Ω = [𝜙𝜙̇𝜃𝜃̇𝜓𝜓̇](II.7)

Vitesses linéaires
Les vitesses linéaires 𝑣𝑣𝑏𝑏, 𝑣𝑣𝑏𝑏, 𝑣𝑣𝑏𝑏 dans le repère fixe en fonction des vitesses linéaires 𝑣𝑣𝑚𝑚, 𝑣𝑣𝑚𝑚, 𝑣𝑣𝑚𝑚 dans le repère mobile sont données par :

Effets physiques agissants sur le quadrotor
Les forces
Les forces agissant sur le système sont :
Le poids du quadrotor: il est donné par P mg, où : m est la masse totale et g la gravité.
Les forces de poussée: qui sont des forces provoquées par la rotation des moteurs, elles sont perpendiculaires sur le plan des hélices. Ces forces sont proportionnelles au carrée de la vitesse de rotation des moteurs :
𝐹𝐹𝑖𝑖 = 𝑏𝑏𝜔𝜔2(II.9)
Avec 𝒊𝒊 = �𝟏𝟏�:�𝟒𝟒�, et b est le coefficient de portance, il dépend de la forme et le nombre des pales et la densité de l’air.
Les forces de traînée : la force de traînée est le couplage entre une force de pression et la force de frottement visqueux, dans ce cas on a deux forces de traînée agissant sur le système qu’elles sont :
La traînée dans les hélices : elle agisse sur les pales, elle est proportionnelle à la densité de l’air, à la forme des pales et au carré de la vitesse de rotation de l’hélice, elle est donnée par la relation suivante :
𝑇𝑇ℎ = 𝑑𝑑𝜔𝜔2(II.10)
Avec d est le coefficient de drag il dépend de la fabrication de l’hélice.
La traînée selon les axes (x, y, z): elle est due au mouvement du corps du quadri-rotor
𝐹𝐹𝑡𝑡 = 𝐾𝐾𝑓𝑓𝑡𝑡𝑣𝑣(II.11)
Avec : 𝑲𝑲𝒇𝒇𝒇𝒇 le coefficient de traînée de translation et 𝝊𝝊 la vitesse linéaire.
Les moments
Il y a plusieurs moments agissants sur le quadrotor, ces moments sont dus aux forces de poussée et de traînée et aux effets gyroscopiques.
Moments dus aux forces de poussée
La rotation autour de l’axe x : elle est due au moment crié par la différence entre les forces de portance des rotors 2 et 4, ce moment est donné par la relation suivante :
𝑀𝑀𝑥𝑥 = (𝐹𝐹4 − 𝐹𝐹2) = 𝑙𝑙(𝜔𝜔2 − 𝜔𝜔2)(II.12)
Avec l, est la longueur du bras entre le rotor et le centre de gravité du quadrotor.
La rotation autour de l’axe y : elle est due au moment crié par la différence entre les forces de portance des rotors 1 et 3, ce moment est donné par la relation suivante :
𝑀𝑀𝑦𝑦 = (𝐹𝐹3 − 𝐹𝐹1) = 𝑙𝑙(𝜔𝜔2 − 𝜔𝜔2)(II.13)
Moments dus aux forces de traînée
La rotation autour de l’axe z : elle est due à un couple réactif provoqué par les couples de traînée dans chaque hélice, ce moment est donné par la relation suivante :
𝑀𝑀𝑧𝑧 = (𝜔𝜔2 − 𝜔𝜔2 + 𝜔𝜔2 − 𝜔𝜔2)(II.14)
Moment résultant des frottements aérodynamiques, il est donné par :
𝑀𝑀𝑎𝑎 = 𝐾𝐾𝑓𝑓𝑎𝑎Ω2(II.15)
Avec 𝐾𝐾𝑓𝑓𝑎𝑎: Le coefficient des frottements aérodynamiques et est la vitesse angulaire.
Effet gyroscopique
L’effet gyroscopique se définit comme la difficulté de modifier la position ou l’orientation du plan de rotation d’une masse tournante.
L’effet gyroscopique est ainsi nommé en référence au mode de fonctionnement du gyroscope, appareil de contrôle de mouvement utilisé dans l’aviation (du grec Gyro qui signifie rotation et scope, observer).
Dans notre cas il y a deux moments gyroscopiques, le premier est le moment gyroscopique des hélices, l’autre est le moment gyroscopique dû aux mouvements de quadrotor.
Moment gyroscopique des hélices : il est donné par la relation suivante :
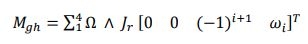 (II.16)
(II.16)
Avec 𝐽𝐽𝑟𝑟 est l’inertie des rotors.
Moment gyroscopique dû aux mouvements de quadri-rotor : il est donné par la relation suivante :
𝑀𝑀𝑔𝑔𝑚𝑚 = Ω ∧ 𝐽𝐽 Ω(II.17)
Avec J est l’inertie du système.
Développement du Modèle mathématique selon Newton-Euler [5-6-7-8]
En utilisant la formulation de Newton-Euler, les équations sont écrites sous la forme suivante:
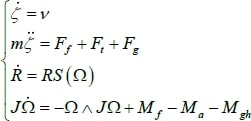
(II.18)
Avec : est le vecteur de position du quadri-rotor
m : la masse totale du quadri-rotor
: La vitesse angulaire exprimée dans le repère fixe
R : La matrice de rotation
: Le produit vectoriel
J : matrice d’inertie symétrique de dimension (3×3), elle est donnée par :
(II.19)
𝑆𝑆(Ω) : est la matrice antisymétrique; pour un vecteur de vélocité Ω = [𝛺𝛺1𝛺𝛺2𝛺𝛺3] , elle est donnée par:
𝐹𝐹𝑓𝑓 : est la force totale générée par les quatre rotors, elle est donnée par :
𝐹𝐹𝑓𝑓 = 𝑅𝑅 × [00∑4 ](II.21)
𝐹𝐹𝑖𝑖 = 𝑏𝑏𝜔𝜔2(II.22)
𝐹𝐹𝑡𝑡 : La force de traînée selon les axes (x, y, z), elle est donnée par :
𝐾𝐾𝑓𝑓𝑡𝑡𝑥𝑥, 𝐾𝐾𝑓𝑓𝑡𝑡𝑦𝑦, 𝐾𝐾𝑓𝑓𝑡𝑡𝑧𝑧 ∶
Les coefficients de traînée de translation,
𝐹𝐹𝑔𝑔 : Force de gravité, elle est donnée par :
𝑀𝑀𝑓𝑓 : Moment provoqué par les forces de poussée et de traînée.1234
𝑀𝑀𝑎𝑎: Moment résultant des frottements aérodynamiques, il est donnée par :
𝐾𝐾𝑓𝑓𝑎𝑎𝑥𝑥𝜙𝜙̇ 2
𝑀𝑀𝑎𝑎 = �𝐾𝐾𝑓𝑓𝑎𝑎𝑦𝑦𝜃𝜃̇2 �(II.26)
𝐾𝐾𝑓𝑓𝑎𝑎𝑧𝑧𝜓𝜓̇ 2
𝐾𝐾𝑓𝑓𝑎𝑎𝑥𝑥, 𝐾𝐾𝑓𝑓𝑎𝑎𝑦𝑦, 𝐾𝐾𝑓𝑓𝑎𝑎𝑧𝑧:
Les coefficients des frottements aérodynamiques.

Equations de mouvement de translation
On a:
𝑚𝑚𝜉𝜉̈ = 𝐹𝐹𝑓𝑓 + 𝐹𝐹𝑡𝑡 + 𝐹𝐹𝑔𝑔(II.27)
On remplace chaque force par sa formule, on trouve :
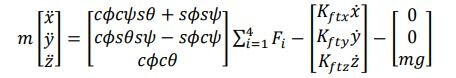
(II.28)
On obtient alors les équations différentielles qui définissent le mouvement de translation :
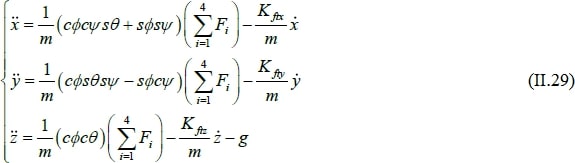
Equation de mouvement de rotation
On a:
𝐽𝐽Ω̇ = −𝑀𝑀𝑔𝑔ℎ − 𝑀𝑀𝑔𝑔ℎ − 𝑀𝑀𝑎𝑎 + 𝑀𝑀𝑓𝑓(II.30)
On remplace chaque moment par la formule correspondant, on trouve :
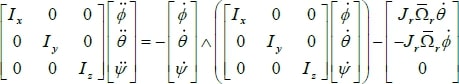
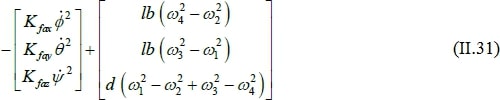
On obtient alors les équations différentielles définissants le mouvement de rotation :
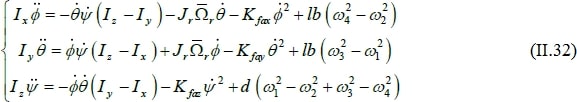
Avec :
�Ω�𝑟𝑟� = 𝜔𝜔1 − 𝜔𝜔2 + 𝜔𝜔3 − 𝜔𝜔4(II.33)
En conséquence, le modèle dynamique complet qui régit le quadrotor est le suivant :
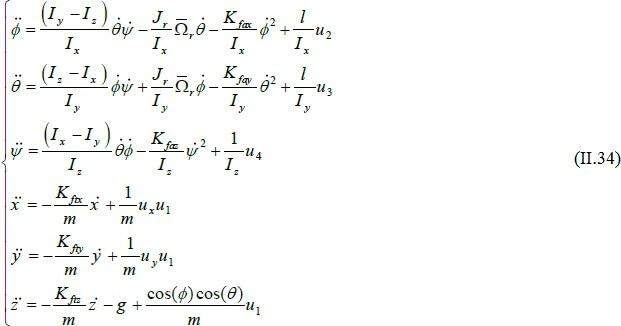
Avec :

Et :
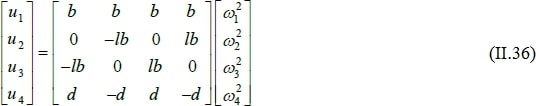
A partir de (II.35), on trouve :
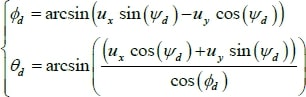
La représentation d’état du système
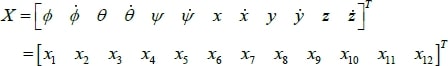
Pour un système physique il existe une multitude de représentations d’état, dans notre cas on choisit le vecteur d’état comme suit [ ] :
On obtient la représentation d’état suivante :
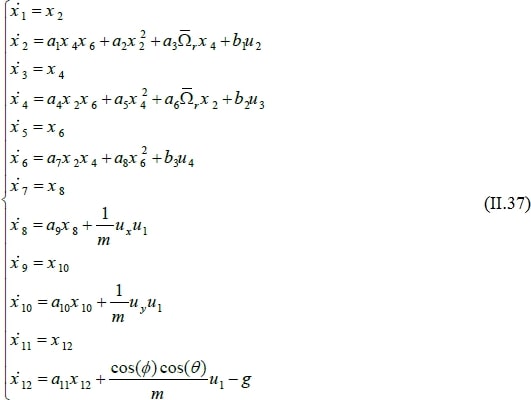
Avec :
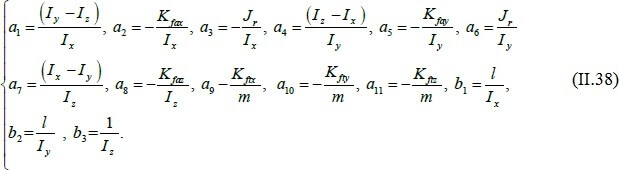
II.2. La dynamique des rotors [1-2]
Généralement les moteurs utilisés dans les quadrotors sont des moteurs à courant alternatif.

La dynamique du rotor est donc approximée à celle d’un moteur à courant alternatif, elle est donnée par les équations différentielles suivantes :
Avec : 𝜏𝜏𝑖𝑖 est le couple d’entrée, et 𝑄𝑄𝑖𝑖 = 𝑑𝑑𝜔𝜔2 est le couple résistant généré par le rotor i.
Pour atteindre les objectifs de la commande d’un quadrotor, une boucle d’asservissement en vitesse est souvent nécessaire.
D’abord, nous avons besoin de déterminer les vitesses désirées 𝜔𝜔𝑑𝑑, correspondantes aux valeurs des commandes fournies par le contrôleur, ces vitesses peuvent être calculées comme suit :
𝜔𝜔�𝑑𝑑 = 𝑀𝑀−1𝑈𝑈(II.40)
Avec: 𝜔𝜔�𝑑𝑑 = (𝜔𝜔2 , 𝜔𝜔2 , 𝜔𝜔2 , 𝜔𝜔2 ), 𝑈𝑈 = (𝑢𝑢1, 𝑢𝑢2, 𝑢𝑢3, 𝑢𝑢4)𝑇𝑇, et 𝑀𝑀 est une matrice non singulière, elle est obtenu à partir de (II.36).
L’objectif est de synthétisé un contrôleur pour que 𝜔𝜔𝑖𝑖 → 𝜔𝜔𝑑𝑑, lorsque 𝑅𝑅 → ∞ en utilisant les couples𝜏𝜏𝑖𝑖.
On définit l’erreur de vitesse :
𝜔𝜔�𝑖𝑖 = 𝜔𝜔𝑖𝑖 − 𝜔𝜔𝑑𝑑,(II.41)
Une loi de commande est développée dans [1-2], elle est donnée par :
𝜏𝜏𝑖𝑖 = 𝑄𝑄𝑖𝑖 + 𝐽𝐽𝑟𝑟 𝜔𝜔̇ 𝑑𝑑, − 𝐾𝐾𝑖𝑖 𝜔𝜔�𝑖𝑖(II.42)
Avec , i 1, 2, 3,4sont des gains positifs.
On remplace la loi de commande dans (II.39), on obtient :
Cette relation représente la dynamique de l’erreur, elle nous montre la convergence exponentielle de 𝜔𝜔𝑖𝑖 vers 𝜔𝜔𝑖𝑖 lorsque𝑅𝑅 → ∞. Sa signifier la convergence des commandes du quadrotor vers ces valeurs désirées, ce qui assure la stabilité du quadrotor (stable drone).
En réalité le quad rotor est commandé par les tensions d’alimentation de ces quatre moteurs. Pour commander ces moteurs, nous avons besoin d’obtenir la tension d’entrée de chaque moteur.
Supposant que l’inductance du moteur est petite, et considérant que les moteurs utilisés sont identiques, nous pouvons obtenir la tension d’entrée de chaque moteur comme suit :
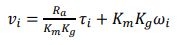 (II.43)
(II.43)
Avec : 𝑅𝑅𝑎𝑎 est la résistance du moteur, 𝐾𝐾𝑚𝑚 est la constant du couple de moteur, 𝐾𝐾𝑔𝑔 est le gain du réducteur.
II.3. Conclusion
Ce chapitre permet au lecteur de comprendre les bases physiques utilisées pour déterminer les équations de la cinétique et la dynamique des quadrotors, ainsi que les forces et les moments agissantes.
L’utilisation du formalisme de Newton-Euler nous a permet d’établir le modèle dynamique du quadrotor.
La complexité du modèle, la non linéarité, et l’interaction entre les états du système, peuvent se voir clairement.
Les résultats des formules précédentes sont utilisés généralement pour établir un modèle mathématique permettant de décrire avec précision le comportement du système.
Dans le prochain chapitre, je vais expliquer brièvement le hardware et le software utilisé dans la réalisation du quadrotor.

