Le modèle de Martingale et modèle du fair game
b. Le modèle de Martingale et du « fair game »
Les critiques faites sur le modèle de marche aléatoire et les problèmes qu’elles posent ont poussé les chercheurs à trouver un autre pouvant être rapproché plus ou moins avec le cadre de l’équilibre économique13.
P. Samuelson (1965) fut le premier à émettre l’idée d’une étude de l’efficience des marchés financiers par le biais du modèle de Martingale en présentant un cadre moins restrictif que le modèle de marche aléatoire. Même si le modèle de Martingale tente d’être plus général et plus large, il est à rappeler qu’il s’approprie largement des arguments du modèle de marche aléatoire.
Et « contrairement à la marche aléatoire, le modèle de Martingale constitue un véritable modèle économique des prix des actifs, dans le sens qu’il peut être lié aux hypothèses primitives sur les préférences et les rendements, qui, bien que restrictives, ne le sont pas à tel point de rendre nécessaire ou évident le besoin de justification économique». [Ibidem, p.24].
– Spécification du modèle de Martingale et du « fair game »
Un processus stochastique Pt est une Martingale conditionnellement à un ensemble d’information Φt, si Pt a la propriété suivante :
![]()
Cela signifie que Pt constitue la prévision optimale de Pt+1, on dit que Pt suit une martingale si et seulement si l’accroissement (Pt+1- Pt) est un « fair game », qui se définit par la relation suivante : ![]()
Ainsi, la prévision de Pt+1, compte tenu de l’information disponible, et quelque soit sa valeur est égale à zéro.
![]()
Cela veut dire que si Pt+1-Pt suit un fair game alors Pt suit une martingale. Les rendements suivent un fair game si et seulement si, la valeur actualisée des revenus futurs composée de gain en capital et de dividendes suivent une martingale.
La valeur actualisée des revenus n’est rien d’autre que la valeur anticipée (prévue) du prix du titre. C’est par ailleurs la valeur fondamentale.
Contrairement au modèle de marche aléatoire ou la valeur fluctue autour de sa valeur fondamentale, dans le modèle de martingale, le prix est supposé égal à la valeur fondamentale. Le modèle de martingale interdit la possibilité de réaliser un profit en spéculant sur la différence entre le prix observé et sa valeur fondamentale.
Une des variantes de ce modèle est :
– Le modèle de sous martingale « submartingal model »
Ce modèle peut être exprimé sous l’une des deux formes suivantes :
![]()
On dira que la séquence des prix suit alors une martingale.
Les limites de ce modèle sont liées aux hypothèses restrictives attachées aux distributions de probabilité et à la stabilité dans le temps de préférence des investisseurs.
c. Le modèle de Processus de retour à la moyenne « mean reversion »
Il existe deux variantes :
– Cas où le processus d’espérance est constant :
Un processus d’espérance constante est décrit par la relation :
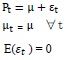
Les prix observés vont présenter une tendance au retour à la moyenne (mean reverting process), si et seulement si, un prix supérieur à la moyenne sera suivi, en moyenne, par un prix inférieur à celle ci.
Bien que les prix eux mêmes soient non corrélés, les changements de prix successifs sont auto corrélés négativement. Ainsi, ce modèle décrit le comportement d’un prix dont on s’attend à ce qu’il soit stable en longue période au niveau μ.
– Cas où le résidu est un processus autorégressifs d’ordre 1
R. J Shiller (1982) et L.H Summers (1986), présentent le modèle de retour à la moyenne, en tant qu’alternatif à celui de martingale en supposant que le processus décrivant les variations des cours des actions est la somme d’une composante permanente et une autre aléatoire.
Le modèle se présente comme suit :
![]()
Où, µt et δt désignent respectivement un bruit blanc et un processus autorégressif d’ordre (1).
La dernière relation implique que le cours observé (évalué par le marché) diffère de sa valeur fondamentale par un facteur multiplicatif approximativement égal à . Deux principales implications peuvent être tirées du modèle de retour à la moyenne et qui semblent, au moins à court terme, contradictoires :
** D’une part, le phénomène de retour à la moyenne signifie qu’il existe une relation stable à long terme entre les cours et les fondamentaux (dividendes) et donc l’hypothèse d’efficience est vérifiée.
** D’autre part, parler d’un phénomène de retour à la moyenne, revient à admettre qu’il existe un écart du moins à court terme, entre les cours observés et leurs valeurs fondamentales; ce qui contredit l’efficience.
Conclusion chapitre 1
Tout au long de ce chapitre on a vu que les notions d’efficience, de rationalité et d’anticipations rationnelles sont au centre du débat sur les théories des marchés financiers.
Le passage en revue de la notion des anticipations rationnelles montre comment se fondent les décisions des différents opérateurs notamment sur la prévision des cours, processus dans lequel l’information et son traitement sont des éléments primordiaux.
On a aussi vu dans ce chapitre que la détention de l’information par les opérateurs de marché constitue un des éléments clés de prise de décision. Avec l’établissement de modèles d’efficience des marchés financiers correspondant au degré d’incorporation de l’information, on voit que cette variable joue un rôle majeur dans le comportement des opérateurs.
On le verra dans le chapitre 2 qui est réservé à l’étude de la forme semi-forte de l’efficience ou l’information est sensée être traitée et incorporée en temps réel par les opérateurs.
Etude de l’efficience semi-forte des marchés financiers : cas de la bourse de Casablanca
Mémoire pour l’obtention du Master en Finance Appliquée
Université Cadi Ayyad de Marrakech – Faculté des sciences juridiques Économiques et sociales
_______________________
13 C’est ce qui justifie surement qu’un certains nombres d’auteurs qui ont étudié le comportement des prix au niveau du marché financier et, ont opté pour l’approche dite des asymétries d’information caractérisée par l’étude de l’équilibre du marché par diverses hypothèses de concurrence parfaite, d’anticipations rationnelles d’information incomplète, de concurrence imparfaite etc..
